A Brief Introduction to Machine Learning
Overview
Teaching: 15 min
Exercises: 5 minQuestions
What is machine learning?
What specific tools will this lesson cover?
Objectives
Give a brief definition of machine learning.
Distinguish between classification and regression models.
Describe the specific methods that this lesson will focus on.
What is Machine Learning?
Broadly speaking, machine learning encompasses a range of techniques and algorithms for gaining insights from large data sets. In this lesson, we will focus on supervised learning for tabular data.
-
Tabular data takes the form of a data frame. The methods we consider can apply to a variety of data frames, from large to very large (e.g., up to 1,000’s of columns/variables and 100,000’s of rows/observations, or more).
-
Supervised learning methods build models that predict output values of a function, given some example input and output values. In our context, the output of this function will typically have the form of one of the columns of our data frame, while the input has the form of the remaining columns.
Given a data frame, we will build machine learning models as follows.
-
Divide the data set into a training set and a testing set. Typically the training set will contain about 60% to 80% of the rows, while the testing set comprises the remaining rows. This train/test split is selected randomly.
-
Train the model on the training set. Part of this process may involve tuning: tweaking various model settings (i.e., hyperparameters) for optimal performance.
-
Test the performance of the model using the testing set. Since the testing set was not used in the training of the model, the testing performance will be a good indication of how well our model will perform on future (unknown) input values.
Once our model is built, we can use it to predict output values from new cases of input, and we can also examine the structure of the model to infer the nature of the relationship between the input and the output.
Example: Kyphosis Data Set
To illustrate the above definitions, consider the kyphosis data set, which is included in the rpart package.
library(rpart)
str(kyphosis)
'data.frame': 81 obs. of 4 variables:
$ Kyphosis: Factor w/ 2 levels "absent","present": 1 1 2 1 1 1 1 1 1 2 ...
$ Age : int 71 158 128 2 1 1 61 37 113 59 ...
$ Number : int 3 3 4 5 4 2 2 3 2 6 ...
$ Start : int 5 14 5 1 15 16 17 16 16 12 ...
For a description of this data set, you can view the help menu for kyphosis.
?kyphosis
For example, in a later episode we will build a model that will predict whether a post-op kyphosis will be present (the output), given the age of the patient, the number of vertebrae involved, and the number of the first vertebra operated on (the input). We will train our model on a selection of rows of this data frame (e.g., about 60 randomly selected rows) and then test it on the remaining rows.
Let’s spend a few minutes exploring this data set.
summary(kyphosis)
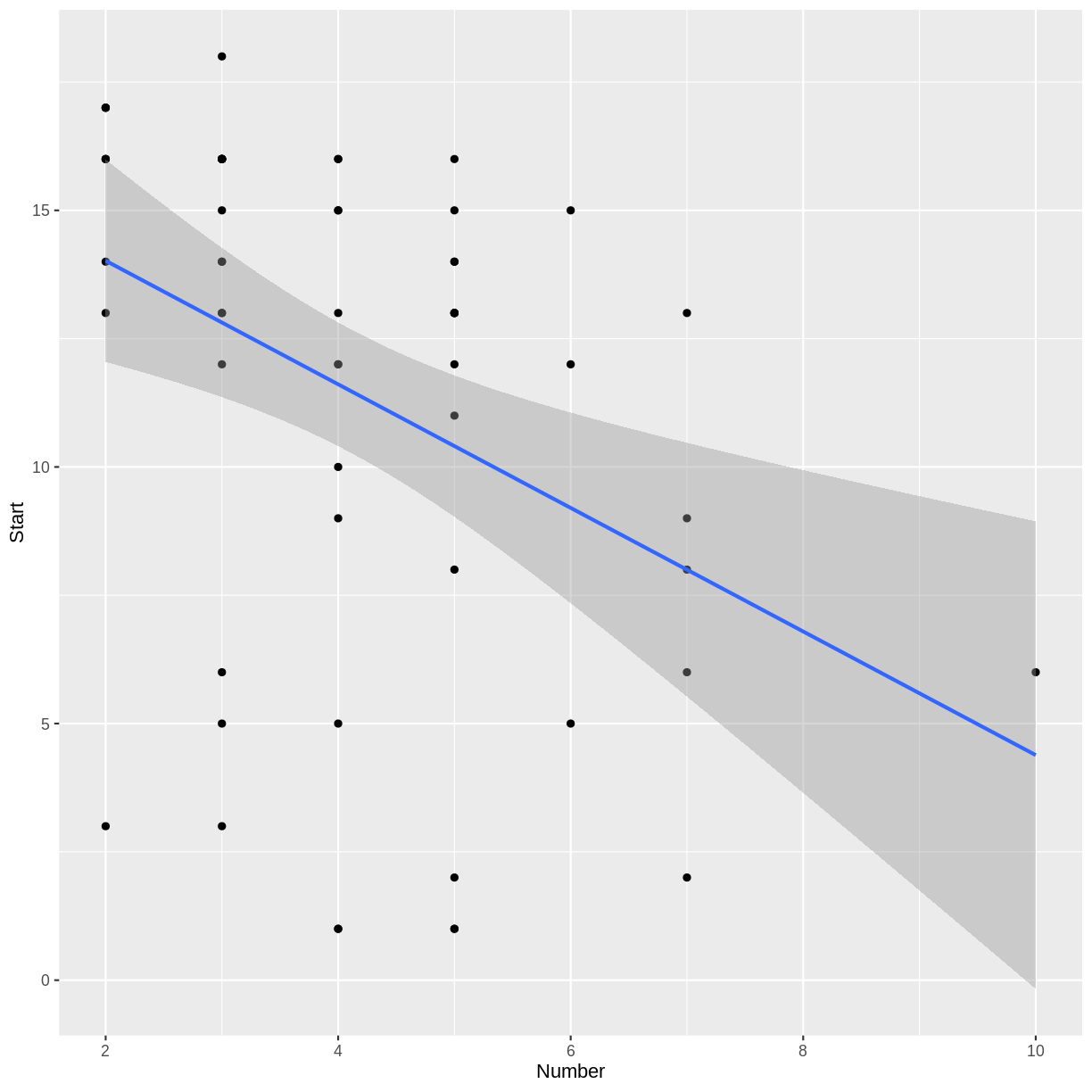
Notice that only 17 of the 81 cases in our data set indicate the presence of a kyphosis. Try making a scatterplot of two of the quantitative variables.
library(tidyverse)
ggplot(kyphosis, aes(x = Number, y = Start)) + geom_point()
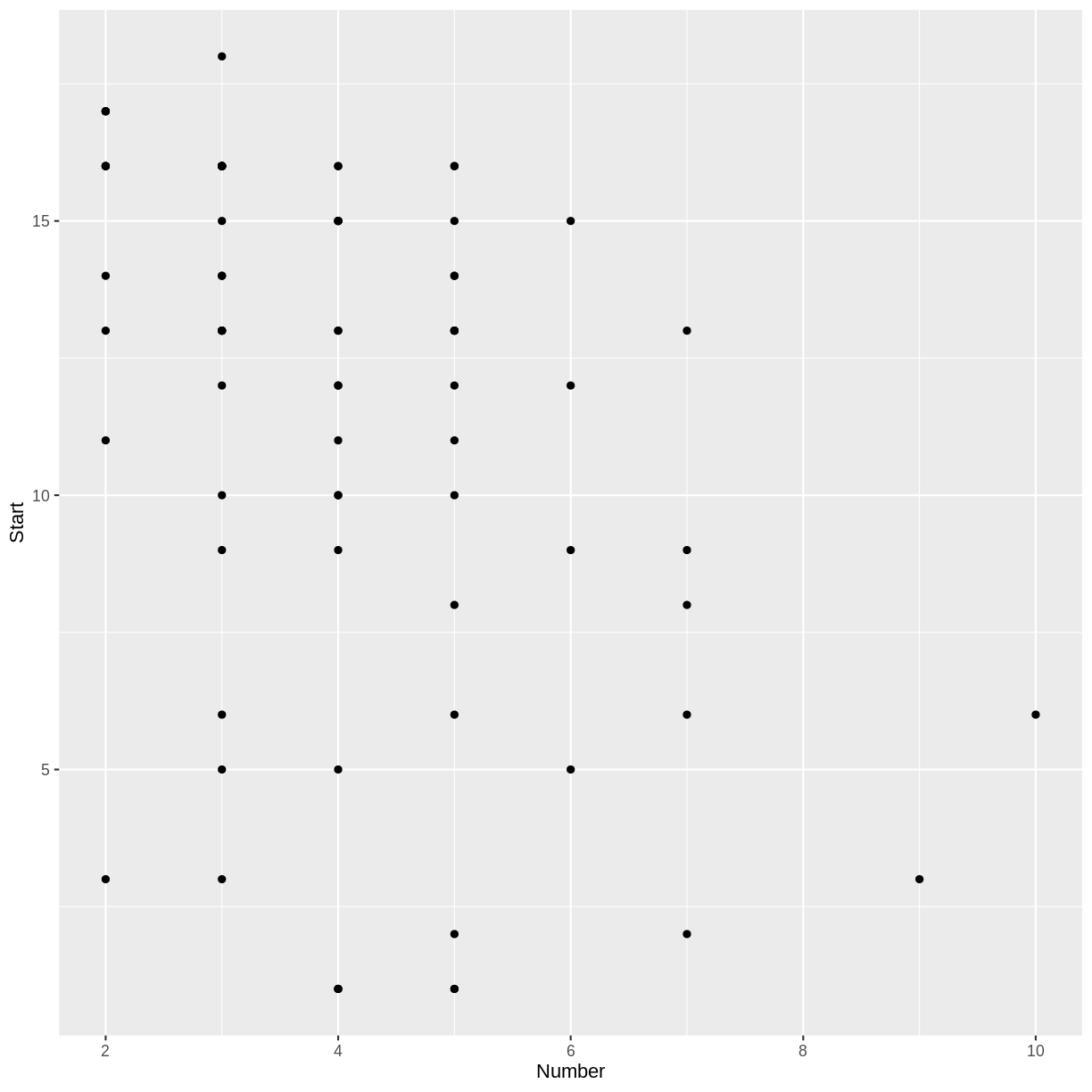
Challenge: Number and Start
Do you notice a trend in the scatterplot of
Startvs.Number? In the context of thekyphosisdata, why would there be such a trend?Solution
There appears to be a weak, negative association between
NumberandStart: larger values ofNumbercorrespond to smaller values ofStart. This correspondence makes sense, because if more vertebrae are involved, the topmost vertebra would have to be higher up. (The vertebrae are numbered starting from the top.)
Classification vs. Regression
In the jargon of machine learning, a model that predicts a categorical output variable is called a classification model, while one that predicts a quantitative (numeric) output is called a regression model. Note: this terminology conflicts slightly with the common use of the term “regression” in statistics.
Our Focus
This lesson will focus on three machine learning methods that apply to both classification and regression problems.
- Decision Trees
- Random Forests
- Gradient Boosted Trees
We will also briefly explore classical linear and logistic regression, which we can view as simple examples of supervised learning. We will not dwell on the mathematical theory or algorithmic details of these methods. Interested learners are encouraged to consult An Introduction to Statistical Learning, by James, Witten, Hastie, and Tibshirani.
One of the main goals of this lesson is to help learners develop their R coding skills, especially for the purpose of using the available machine learning packages on the Comprehensive R Archive Network (CRAN). We will focus on the packages randomForest and xgboost, but many other packages are described in the CRAN Machine Learning Task View.
Key Points
There are many types of machine learning.
We will focus on some methods that work well with tabular data.
Linear and Logistic Regression
Overview
Teaching: 35 min
Exercises: 15 minQuestions
How can a model make predictions?
How do we measure the performance of predictions?
Objectives
Define a linear regression model.
Define a logistic regression model.
Split data into training and testing sets.
Kyphosis Data
Make sure the rpart package is loaded, and examine the structure of the kyphosis data frame.
library(rpart)
str(kyphosis)
'data.frame': 81 obs. of 4 variables:
$ Kyphosis: Factor w/ 2 levels "absent","present": 1 1 2 1 1 1 1 1 1 2 ...
$ Age : int 71 158 128 2 1 1 61 37 113 59 ...
$ Number : int 3 3 4 5 4 2 2 3 2 6 ...
$ Start : int 5 14 5 1 15 16 17 16 16 12 ...
Notice that there are 81 observations of four variables, so this is a rather small data set for machine learning techniques. In this episode, we will use this data set to illustrate the process of training and testing, where our models will be built using classical linear and logistic regression.
Make a training set and a test set
The first step in the process is to create a random train/test split of our data set. We will use the training set to build our model, without looking at the testing set. After our model is built, we will measure the accuracy of its predictions using the testing set.
There are various R packages that automate common tasks in machine learning, but it is instructive to use base R for now. The following commands will randomly select the row indexes of the training set (and therefore also of the testing set).
trainSize <- round(0.75 * nrow(kyphosis))
set.seed(6789) # so we all get the same random sets
trainIndex <- sample(nrow(kyphosis), trainSize)
Take a look at the trainIndex variable in the Environment tab of RStudio. Since we set a particular value for the random seed, we should all see the same sample of random numbers.
Next we form two data frames using these indexes. Recall that the selection of -trainIndex will select all rows whose indexes are not in the trainIndex vector.
trainDF <- kyphosis[trainIndex, ]
testDF <- kyphosis[-trainIndex, ]
We can View the train and test sets in RStudio to check that they form a random partition of the kyphosis data.
View(trainDF)
View(testDF)
Linear Regression as Supervised Learning
In the previous episode, we constructed a scatterplot of Number versus Start and observed a slight negative association. A model of this relationship is given by the least squares regression line, which we can consider as a simple example of supervised learning. To compute the slope and y-intercept of this line, we use the lm function in R.
In the following code block, the formula Start ~ Number specifies that Number is the explanatory (independent) variable, and Start is the response (dependent) variable. A helpful mnemonic is to read the ~ symbol as “as explained by.” To illustrate the process of supervised learning, we fit this regression line to the training set trainDF, saving the testing set for later.
model1 <- lm(Start ~ Number, data = trainDF)
summary(model1)
Call:
lm(formula = Start ~ Number, data = trainDF)
Residuals:
Min 1Q Median 3Q Max
-11.018 -1.610 1.615 3.186 5.798
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.4268 1.6393 10.021 2.38e-14 ***
Number -1.2041 0.3721 -3.236 0.00199 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.698 on 59 degrees of freedom
Multiple R-squared: 0.1507, Adjusted R-squared: 0.1364
F-statistic: 10.47 on 1 and 59 DF, p-value: 0.001988
The predicted Start is obtained by multiplying Number by the regression slope -1.2041 and adding the intercept 16.4268.
Challenge: Make a prediction and plot the regression line
- Predict the starting vertebra when the number of vertebrae involved is 3.
- Adding the term
geom_smooth(method = "lm")to a scatterplot will produce a plot of the regression line. Modify theggplotcode from the previous episode to create a scatterplot of the training data, along with a regression line.Solution
Three times -1.2041 plus 16.4268 is approximately 12.81.
library(ggplot2) # don't need this line if tidyverse is already loaded ggplot(trainDF, aes(x = Number, y = Start)) + geom_point() + geom_smooth(method = "lm")
Try the Testing Data Set
In R there is a generic method called predict that will make predictions given models of various types. For example, we can compute the predicted starting vertebrae for all the cases in our testing set as follows.
predictedStart <- predict(model1, testDF)
Challenge: Check our prediction
Check that the result of the
predictfunction agrees with the result of the previous challenge.Solution
head(predictedStart)12 21 32 36 37 38 12.81438 14.01851 14.01851 12.81438 12.81438 10.40611head(testDF)Kyphosis Age Number Start 12 absent 148 3 16 21 absent 22 2 16 32 absent 125 2 11 36 absent 93 3 16 37 absent 1 3 9 38 present 52 5 6Notice that the first row of our testing set has a
Numbervalue of 3, and the first value ofpredictedStartagrees with our answer to the previous challenge.
In general, the value of Start predicted by the model will not equal the actual value of Start in the testing set. However, in a good model, we would hope that the predicted values will be close to the actual values. To assess how close our predictions are to reality, we compute a vector of errors: predicted values minus actual values.
actualStart <- testDF$Start
errors <- predictedStart - actualStart
cat(round(errors, 1))
-3.2 -2 3 -3.2 3.8 4.4 0.2 2.6 10.6 2.8 -3.4 0.4 -3 -0.2 -0.2 1.6 -1.4 0.6 -5.6 -3.4
Measuring the Prediction Error
There are several ways to summarize the overall error in a regression model. The mean of the errors is not a good choice, because errors will usually have positive and negative values, which will cancel when averaged. To avoid this cancellation effect, we can take the mean of the squares of the errors: the Mean Squared Error, or MSE.
mean(errors^2)
[1] 13.14172
For a measurement of overall error in the same units as the output variable, we take the square root of the MSE to obtain the Root Mean Squared Error, or RMSE.
sqrt(mean(errors^2))
[1] 3.625151
Challenge: Mean Absolute Error
The Mean Absolute Error (MAE) is the average of the absolute values of the errors. Compute the MAE for the above example.
Solution
mean(abs(errors))[1] 2.77752
In upcoming episodes, we will compare different regression models using the RMSE of the prediction error on the testing set.
Logistic Regression
In the previous episode, we observed that in the context of the kyphosis data, it would be natural to try to predict whether a post-op kyphosis will be present, given the age of the patient, the number of vertebrae involved, and the number of the first vertebra operated on. In this situation, Kyphosis is our categorical response variable, and Age, Number, and Start are the explanatory variables. You can see the levels of the Kyphosis variable with the following command.
levels(kyphosis$Kyphosis)
[1] "absent" "present"
Since our response variable is categorical, we need to employ a classification model. The following command will fit a Multiple Logistic Regression model to our training data using the glm command.
model2 <- glm(Kyphosis ~ Age + Number + Start, data = trainDF, family = "binomial")
Notice that we specified the formula Kyphosis ~ Age + Number + Start, because Kyphosis is the response variable and Age, Number, and Start are the explanatory variables. Since Age, Number, and Start make up all the remaining columns in our data frame, we could have used the equivalent formula Kyphosis ~ ., as follows.
model2 <- glm(Kyphosis ~ ., data = trainDF, family = "binomial")
The formula Kyphosis ~ . can be read as “Kyphosis as explained by everything else.”
The predict function for binomial glm models will return predicted probabilities of the response variable if we specify the option type = "response".
predict(model2, testDF, type = "response")
12 21 32 36 37 38
0.060991556 0.004837329 0.066676823 0.027771160 0.034862103 0.389677526
39 43 44 46 47 51
0.287882930 0.988363673 0.531083119 0.183999574 0.122064478 0.244337950
52 57 60 66 68 69
0.003170923 0.014410381 0.061131542 0.069057143 0.236889844 0.056456800
70 76
0.035581184 0.206575349
If we actually want to know whether or not the model predicts that a kyphosis is present, we need to convert these probabilities to the appropriate levels of the Kyphosis variable.
The first level, absent, corresponds to probabilities near zero, and the second level, present, corresponds to probabilities near one. So we can create a vector of the predicted Kyphosis values of our testing set as follows.
predictedKyphosis <- ifelse(predict(model2, testDF, type = "response") < 0.5,
"absent", "present")
predictedKyphosis
12 21 32 36 37 38 39 43
"absent" "absent" "absent" "absent" "absent" "absent" "absent" "present"
44 46 47 51 52 57 60 66
"present" "absent" "absent" "absent" "absent" "absent" "absent" "absent"
68 69 70 76
"absent" "absent" "absent" "absent"
The actual occurrences of kyphosis in our testing set are given by the vector testDF$Kyphosis, so the following command will tell us which predictions were correct.
testDF$Kyphosis == predictedKyphosis
12 21 32 36 37 38 39 43 44 46 47 51 52
TRUE TRUE TRUE TRUE TRUE FALSE TRUE FALSE FALSE FALSE TRUE TRUE TRUE
57 60 66 68 69 70 76
TRUE TRUE TRUE TRUE TRUE TRUE TRUE
One way to measure the performance of a classification model is to report the proportion of correct predictions, known as the accuracy of the model. Recall that the sum function, when applied to a logical vector, will return the number of TRUEs in the vector.
accuracy <- sum(testDF$Kyphosis == predictedKyphosis)/nrow(testDF)
cat("Proportion of correct predictions using testing data: ", accuracy, "\n")
Proportion of correct predictions using testing data: 0.8
cat("Testing data error rate: ", 1-accuracy, "\n")
Testing data error rate: 0.2
Challenge: Try different train/test splits
Before we constructed the models in this episode, we divided the data into a training set and a testing set. Try experimenting with different train/test splits to see if it has any effect on the model accuracy. Specifically, re-do the construction of
model2, the logistic regression model, with the following modifications.
Try a different value of the random seed. Does the prediction accuracy change?
We originally chose a training set size that was 75% of the size of the
kyphosisdata frame. Experiment with different percentages for the train/test split. Does changing the size of the training set affect the accuracy of the model?Solution
Let’s define a function to avoid repeating code.
testAccuracy <- function(splitPercent, randomSeed) { tSize <- round(splitPercent * nrow(kyphosis)) set.seed(randomSeed) tIndex <- sample(nrow(kyphosis), tSize) trnDF <- kyphosis[tIndex, ] tstDF <- kyphosis[-tIndex, ] kmod <- glm(Kyphosis ~ ., data = trnDF, family = "binomial") predK <- ifelse(predict(kmod, tstDF, type = "response") < 0.5, "absent", "present") return(sum(tstDF$Kyphosis == predK)/nrow(tstDF)) }Try different seeds:
testAccuracy(0.75, 6789) # our original settings[1] 0.8testAccuracy(0.75, 1234)[1] 0.9So the choice of seed makes a difference.
Try different split percentages:
testAccuracy(0.9, 6789)[1] 0.75testAccuracy(0.5, 6789)[1] 0.7804878
Key Points
Classical linear and logistic regression models can be thought of as examples of regression and classification models in machine learning.
Testing sets can be used to measure the performance of a model.
Decision Trees
Overview
Teaching: 40 min
Exercises: 15 minQuestions
What are decision trees?
How can we use a decision tree model to make a prediction?
What are some shortcomings of decision tree models?
Objectives
Introduce decision trees and recursive partitioning.
Revisit the Kyphosis example using a classification tree.
Illustrate the use of training and testing sets.
Decision Trees
Let’s simulate a data set of exam scores, along with letter grades.
library(tidyverse)
set.seed(456)
exam <- tibble(score = sample(80:100, 200, replace = TRUE)) %>%
mutate(grade = as_factor(ifelse(score < 90, "B", "A")))
head(exam)
summary(exam)
Given only this data frame, can we recover the grading scale that was used to assign the letter grades? In other words, can we partition this data set into A’s and B’s, based on the exam score? The rpart command can form this partition for us, using the formula syntax we saw in the last episode.
library(rpart)
library(rpart.plot)
examTree <- rpart(grade ~ score, data = exam)
rpart.plot(examTree)
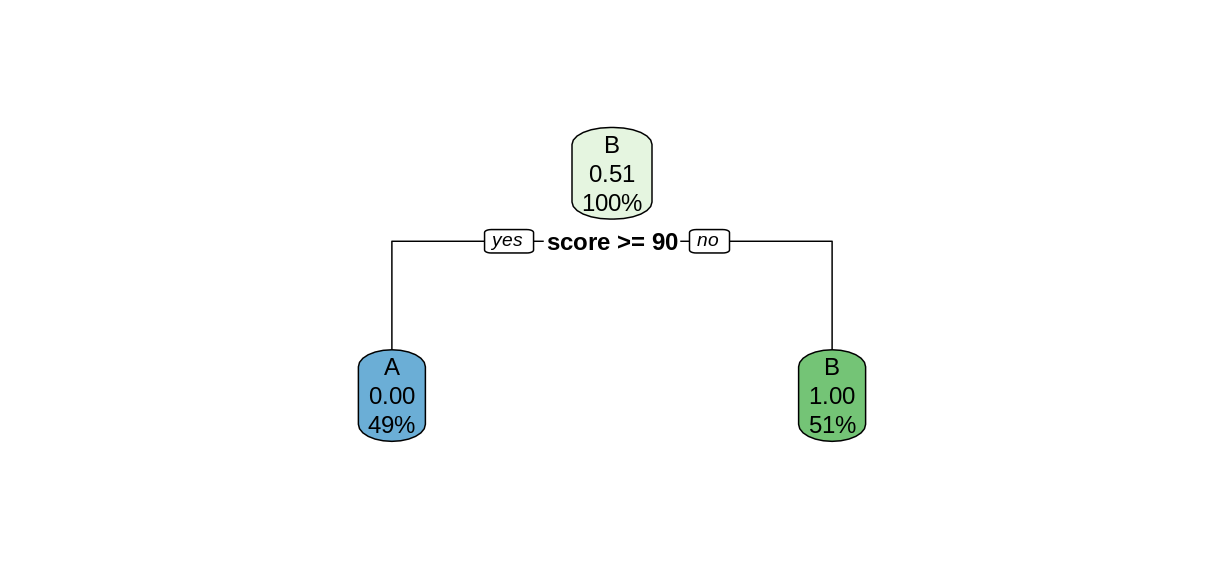
The rpart function searches for the best way to split the data set into predicted values of the response variables, based on the explanatory variables. This Introduction to Rpart has details on how the split is chosen. In this simple case, the rpart function was able to perfectly partition the data after only one split. We can tell rpart.plot to report the number of correctly-classified cases in each node by including the option extra = 2.
rpart.plot(examTree, extra = 2)
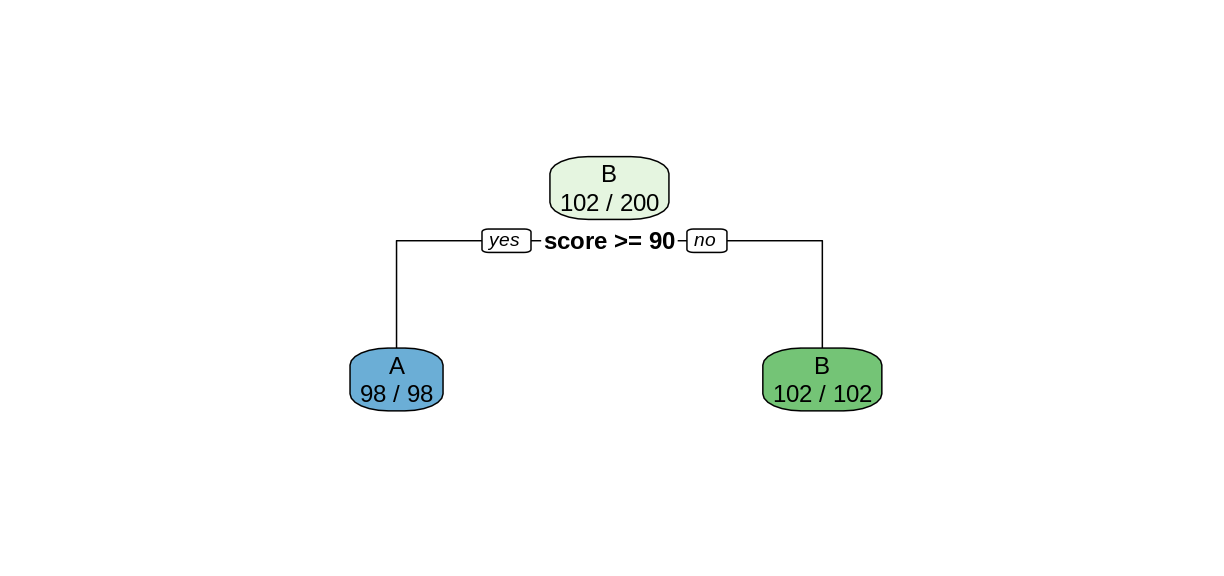
Notice that in the top node, every case was classified as a B, so only the Bs were correctly classified. After the split, both child nodes were classified perfectly.
In more complex situations, the algorithm will continue to create further splits to improve its classification. This process is called recursive partitioning.
Challenge: Use
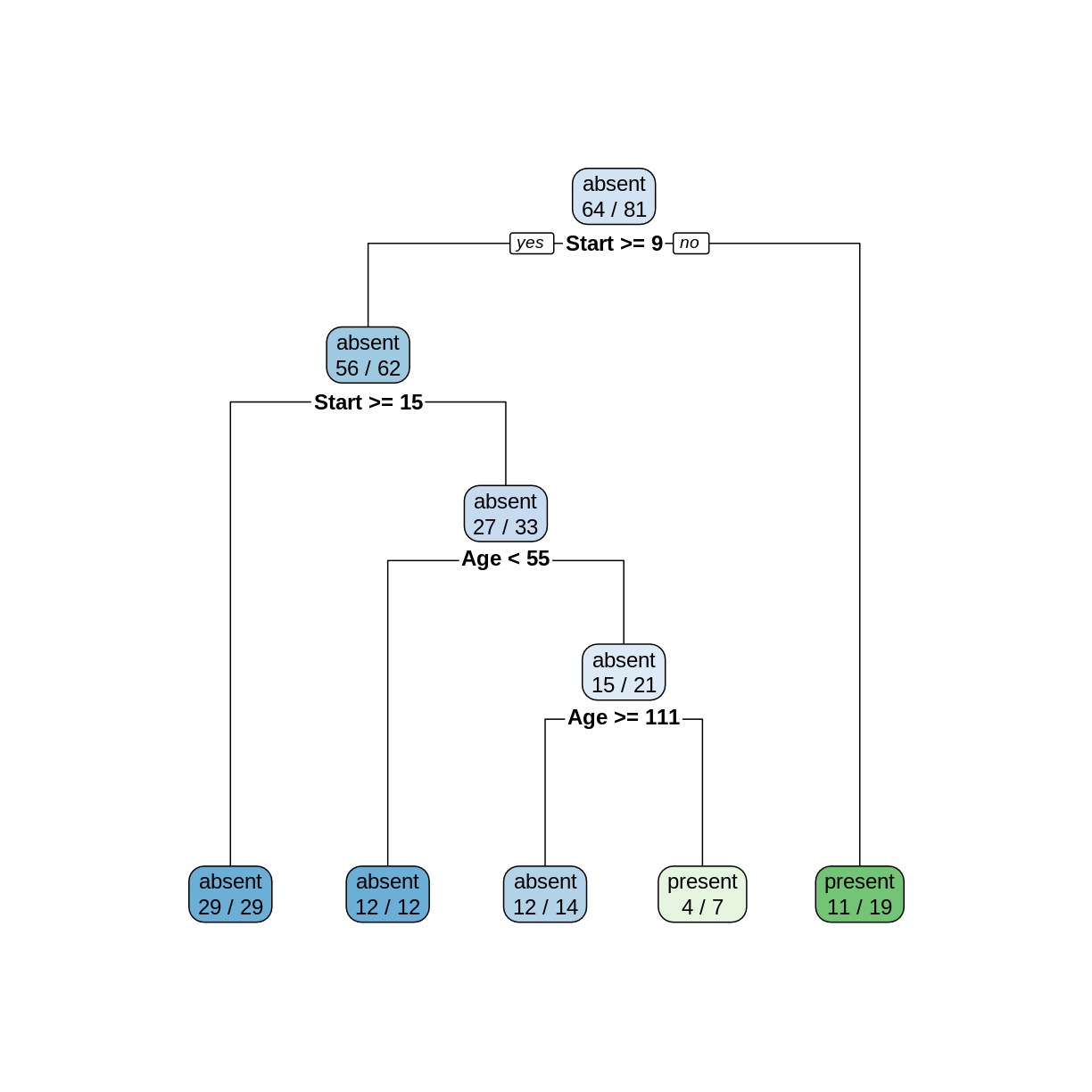
rparton thekyphosisdataUse the
rpartfunction to create a decision tree using thekyphosisdata set. As in the previous episode, the response variable isKyphosis, and the explanatory varables are the remaining columnsAge,Number, andStart.
- Use
rpart.plotto plot your tree model.- Use this tree to predict the value of
KyphosiswhenStartis 12,Ageis 59, andNumberis 6.- How many of the 81 cases in the data set does this tree classify incorrectly?
Solution
ktree <- rpart(Kyphosis ~ ., data = kyphosis) rpart.plot(ktree, extra = 2)
To make a prediction using this tree, start at the top node. Since
Startis 12, and 12 >= 9, we follow the left (yes) edge. SinceStartis not >= 15, we then follow the right (no) edge. SinceAgeis 59 and 59 is not < 55, we follow the right edge. Finally, sinceAgeis not >= 111 we follow the right edge to the leaf and obtain the predictionpresent.In the two leftmost leaves, all of the cases are classified correctly. However, in the three remaining leaves, there are 2, 3, and 8 incorrectly classified cases, for a total of 13 misclassifications.
Using Decision Trees for Supervised Learning
In order to compare the decision tree model to the logistic regression model in the previous episode, let’s train the model on the training set and test in on the testing set. The following commands will form our training and testing set using the slice function, which is part of the tidyverse.
trainSize <- round(0.75 * nrow(kyphosis))
set.seed(6789) # same seed as in the last episode
trainIndex <- sample(nrow(kyphosis), trainSize)
trainDF <- kyphosis %>% slice(trainIndex)
testDF <- kyphosis %>% slice(-trainIndex)
Now train the decision tree model on the training set
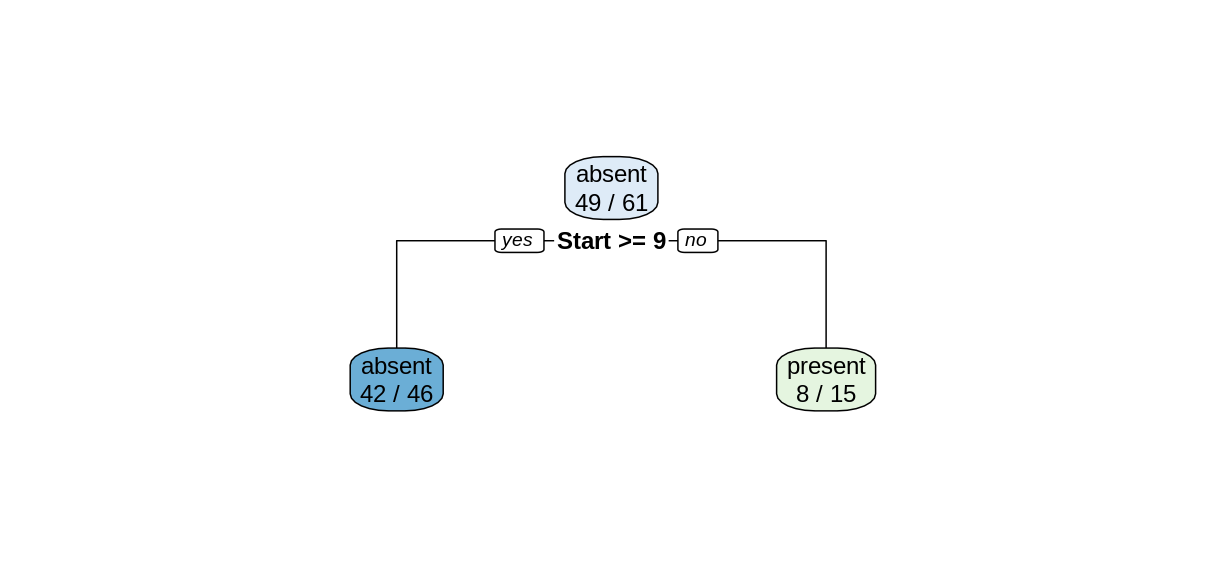
treeModel <- rpart(Kyphosis ~ Age + Number + Start, data = trainDF)
rpart.plot(treeModel, extra = 2)
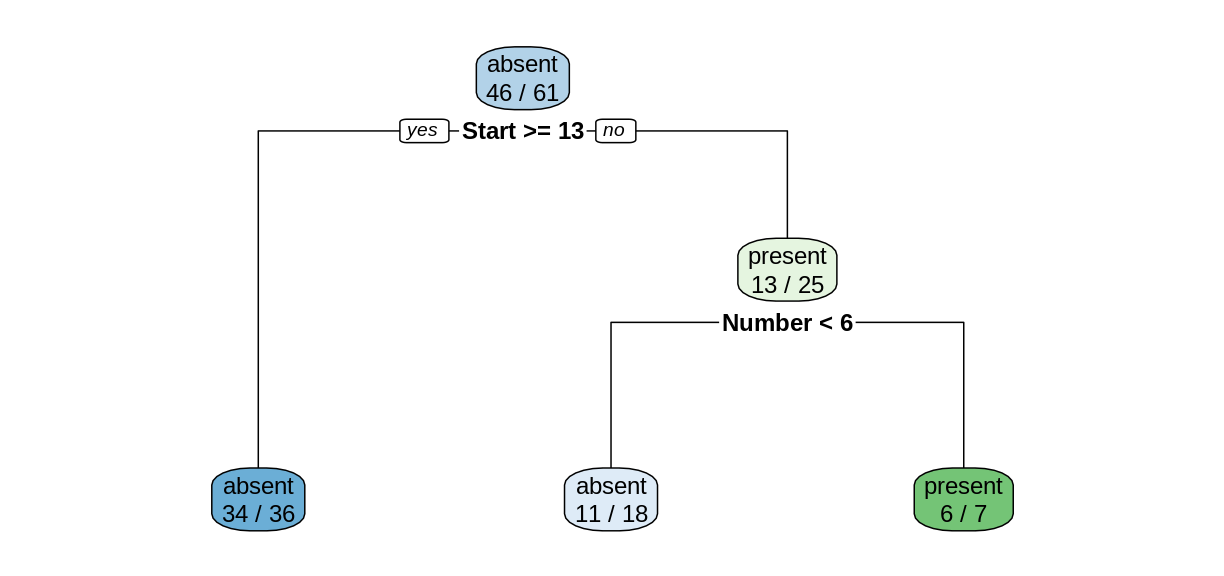
Notice that we obtain a simpler tree using the training set instead of the full data set.
Challenge: Training set accuracy
What proportion of cases in the training set were classified correctly?
Solution
Reading the leaves from left to right, there were 34, 11, and 6 correctly-classified cases:
(34+11+6)/nrow(trainDF)[1] 0.8360656
Model predictions on the testing set
The predict function works on rpart models similarly to how it works on lm and glm models, but the output is a matrix of predicted probabilities.
predict(treeModel, testDF)
absent present
1 0.9444444 0.05555556
2 0.9444444 0.05555556
3 0.6111111 0.38888889
4 0.9444444 0.05555556
5 0.6111111 0.38888889
6 0.6111111 0.38888889
7 0.1428571 0.85714286
8 0.1428571 0.85714286
9 0.6111111 0.38888889
10 0.6111111 0.38888889
11 0.9444444 0.05555556
12 0.6111111 0.38888889
13 0.9444444 0.05555556
14 0.9444444 0.05555556
15 0.9444444 0.05555556
16 0.6111111 0.38888889
17 0.9444444 0.05555556
18 0.6111111 0.38888889
19 0.9444444 0.05555556
20 0.9444444 0.05555556
To investigate the behavior of this model, we bind the columns of the predicted probabilities to the testing set data frame to create a new data frame called predDF.
predMatrix <- predict(treeModel, testDF)
predDF <- testDF %>%
bind_cols(predMatrix)
Challenge: Predicted probabilities
Compare the results in the
predDFdata frame with the plot oftreeModel. Can you explain how the model is calculating the predicted probabilites?Solution
Consider the first row of
predDF.predDF[1,]Kyphosis Age Number Start absent present 1 absent 148 3 16 0.9444444 0.05555556Since the value of
Startis greater than 13, we follow the “yes” branch of the decision tree and land at the leftmost leaf, labeled “absent”, with a probability of 34/36, which is approximately 0.9444. Similarly, consider row 8.predDF[8,]Kyphosis Age Number Start absent present 8 absent 143 9 3 0.1428571 0.8571429Since the value of
Startis less than 13, we follow the “no” branch. Then since the value ofNumberis greater than 6, we follow the right branch to land on the leaf labeled “present”, with a probability of 6/7, which is 0.8571.
Testing set accuracy
Let’s add a new column called Prediction to the predDF data frame that gives the model prediction (absent or present) for each row, based on the probability in the absent column of predDF.
predDF <- predDF %>%
mutate(Prediction = ifelse(predDF$absent > 0.5, "absent", "present"))
Recall that in supervised learning, we use the testing set to measure how our model performs on data it was not trained on. Since this model is a classification model, we compute accuracy as the proportion of correct predictions.
accuracy <- sum(predDF$Kyphosis == predDF$Prediction)/nrow(predDF)
cat("Proportion of correct predictions: ", accuracy, "\n")
Proportion of correct predictions: 0.8
In general, the accuracy on the testing set will be less than the accuracy on the training set.
Challenge: Change the training set
Repeat the construction of the decision tree model for the
kyphosisdata, but experiment with different values of the random seed to obtain different testing and training sets. Does the shape of the tree change? Does the testing set accuracy change?Solution
set.seed(314159) # try a different seed trainIndex <- sample(nrow(kyphosis), trainSize) # use the same size training set trainDF <- kyphosis %>% slice(trainIndex) testDF <- kyphosis %>% slice(-trainIndex) treeModel <- rpart(Kyphosis ~ Age + Number + Start, data = trainDF) rpart.plot(treeModel, extra = 2)
Changing the seed for the train/test split resulted in a different decision tree.
predMatrix <- predict(treeModel, testDF) predictedKyphosis <- ifelse(predMatrix[,1] > 0.5, "absent", "present") accuracy <- sum(testDF$Kyphosis == predictedKyphosis)/nrow(testDF) cat("Proportion of correct predictions: ", accuracy, "\n")Proportion of correct predictions: 0.85The testing set accuracy also changed.
Robustness, or lack thereof
In this episode we have seen that the structure of the decision tree can vary quite a bit when we make small changes to the training data. Training the model on the whole data set resulted in a very different tree than what we obtained by training on a slightly smaller testing set. And changing the choice of testing set, even while maintaining its size, also altered the tree structure. When the structure of a model changes significantly for a small change in the training data, we say that the model is not robust. Non-robustness can be a problem, because one or two unusual observations can make a big difference in the conclusions we draw.
Since their predictions can vary wildly depending on the randomly selected training set, decision trees are called weak learners. In the upcoming episodes, we will explore two methods that use ensembles of weak learners to create a models with more predictive strength.
Key Points
Training data can give us a decision tree model.
Decision trees can be used for supervised learning, but they are not very robust.
Random Forests
Overview
Teaching: 60 min
Exercises: 30 minQuestions
What are random forests?
How do random forests improve decision tree models?
Objectives
Introduce random forests.
Use random forests for classification and regression models.
Evaluate the quality of a random forest model.
We saw in the previous episode that decision tree models can be sensitive to small changes in the training data. Random Forests mitigate this issue by forming an ensemble (i.e., set) of decision trees, and using them all together to make a prediction.
Wine Dataset
For this episode, we will use a data set described in the article Modeling wine preferences by data mining from physicochemical properties, in Decision Support Systems, 47(4):547-553, by P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis. (Instructions for downloading this data set are in the setup page.) The data set contains quality ratings and measurements from 6497 samples of wine; rows 1:1599 are red wine samples, and rows 1600:6497 are white wine.
library(tidyverse)
library(here)
wine <- read_csv(here("data", "wine.csv"))
glimpse(wine)
Rows: 6,497
Columns: 12
$ fixed.acidity <dbl> 7.4, 7.8, 7.8, 11.2, 7.4, 7.4, 7.9, 7.3, 7.8, 7.5…
$ volatile.acidity <dbl> 0.700, 0.880, 0.760, 0.280, 0.700, 0.660, 0.600, …
$ citric.acid <dbl> 0.00, 0.00, 0.04, 0.56, 0.00, 0.00, 0.06, 0.00, 0…
$ residual.sugar <dbl> 1.9, 2.6, 2.3, 1.9, 1.9, 1.8, 1.6, 1.2, 2.0, 6.1,…
$ chlorides <dbl> 0.076, 0.098, 0.092, 0.075, 0.076, 0.075, 0.069, …
$ free.sulfur.dioxide <dbl> 11, 25, 15, 17, 11, 13, 15, 15, 9, 17, 15, 17, 16…
$ total.sulfur.dioxide <dbl> 34, 67, 54, 60, 34, 40, 59, 21, 18, 102, 65, 102,…
$ density <dbl> 0.9978, 0.9968, 0.9970, 0.9980, 0.9978, 0.9978, 0…
$ pH <dbl> 3.51, 3.20, 3.26, 3.16, 3.51, 3.51, 3.30, 3.39, 3…
$ sulphates <dbl> 0.56, 0.68, 0.65, 0.58, 0.56, 0.56, 0.46, 0.47, 0…
$ alcohol <dbl> 9.4, 9.8, 9.8, 9.8, 9.4, 9.4, 9.4, 10.0, 9.5, 10.…
$ quality <dbl> 5, 5, 5, 6, 5, 5, 5, 7, 7, 5, 5, 5, 5, 5, 5, 5, 7…
ggplot(wine, aes(x = quality)) + geom_histogram(binwidth = 1)
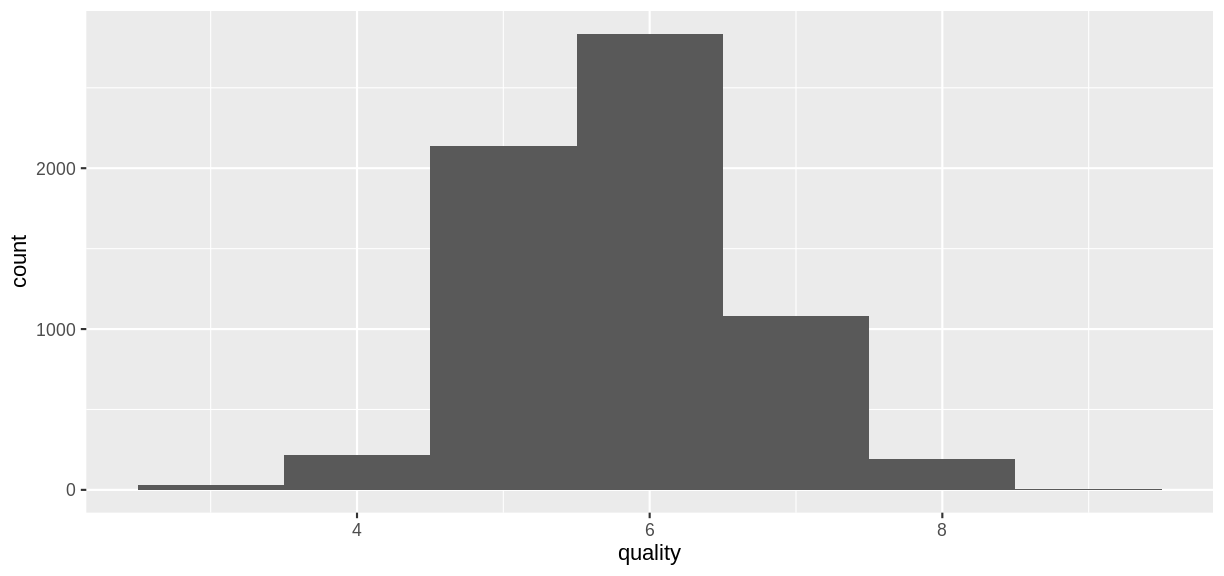The goal of the models that follow will be to predict the quality rating of a wine sample from its chemical properties.
Red Wine Classification Model
To illustrate classification models with this data set, let’s create a categorical variable grade that will serve as a response variable.
redwineClass <- wine %>%
slice(1:1599) %>% # just the red wine samples
mutate(grade = as_factor(if_else(quality < 5.5, "bad", "good"))) %>%
select(-quality) # get rid of the quality variable
summary(redwineClass$grade)
bad good
744 855
Create Training and Test Sets
Create training and test sets using an 80/20 split.
trainSize <- round(0.80 * nrow(redwineClass))
set.seed(1234)
trainIndex <- sample(nrow(redwineClass), trainSize)
trainDF <- redwineClass %>% slice(trainIndex)
testDF <- redwineClass %>% slice(-trainIndex)
Challenge: Create a decision tree model
Use the
rpartfunction to create a decision tree model for predicting thegradevariable from the remaining columns in theredwineClassdata frame. Use the training and testing sets defined above. Compute the testing set accuracy.Solution
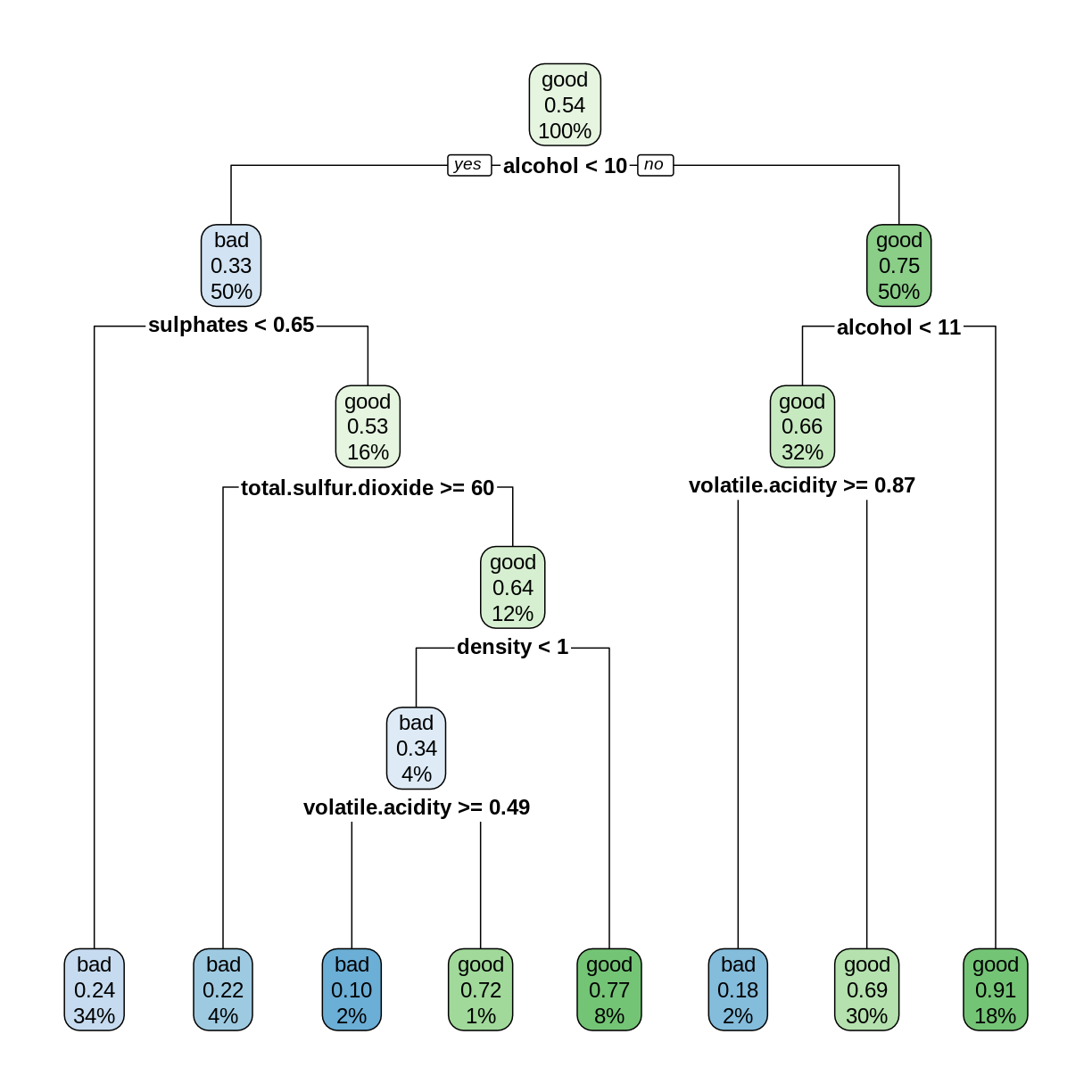
library(rpart) library(rpart.plot) rwtree <- rpart(grade ~ ., data = trainDF) rpart.plot(rwtree)
rwp <- predict(rwtree, testDF) rwpred <- ifelse(rwp[,1] > 0.5, "bad", "good") sum(testDF$grade == rwpred)/nrow(testDF)[1] 0.696875The decision tree model can correctly predict the grade about 70% of the time.
Random Forest Classification Model
A random forest model combines several decision tree models as follows.
- Several different decision trees are built, each from a random bootstrap sample of the same size as the original data. This process is also known as bagging (bootstrap aggregation).
- For each tree model, a randomly-chosen subset of variables is chosen to determine each split.
- Each decision tree model makes a prediction, and the category with the most “votes” is selected as the prediction of the random forest.
More details can be found in Breiman’s 2002 paper, pages 8-9.
The randomForest package is an R implementation of Breiman and Cutler’s original Fortran code. The syntax for building a model is similar to lm, glm, and rpart. Because of the randomness used in the algorithm, it is good practice to set the random seed so that the results will be reproducible.
library(randomForest)
set.seed(4567)
redwineForest <- randomForest(grade ~ ., data = trainDF)
The predict function works on random forests. Observe that it returns a vector of levels of the grade variable.
rwpred2 <- predict(redwineForest, testDF)
head(rwpred2)
1 2 3 4 5 6
bad bad bad bad bad bad
Levels: bad good
Challenge: Accuracy of the Random Forest Model
Compute the testing set accuracy of the random forest model above. Compare this accuracy with the decision tree model in the previous challenge.
Solution
sum(testDF$grade == rwpred2)/nrow(testDF)[1] 0.821875The random forest model can correctly predict the grade about 82% of the time, which is an improvement of about 12 percentage points over the decision tree model.
Out-of-bag Error
Since each tree in the random forest is built on a bootstrap sample of the rows in the training set, some rows will be left out of each sample. Each tree can then make a prediction on each row that was excluded, i.e., “out of the bag” (OOB). Each row will be excluded by several trees, which form a subforest that produces an aggregate prediction for each row. The out-of-bag estimate of the error rate is the error rate of these predictions. The OOB error rate gives a convenient estimate of the error rate of the model (error = 1 - accuracy). The print function reports the OOB error.
print(redwineForest)
Call:
randomForest(formula = grade ~ ., data = trainDF)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 19.16%
Confusion matrix:
bad good class.error
bad 470 119 0.2020374
good 126 564 0.1826087
The confusion matrix gives further details on how the OOB error was calculated: Out of 470+119 bad wines, 119 were classified as good, and out of 126+564 good wines, 126 were classified as bad. Check that (119+126)/(470+119+126+564) = 0.1916.
Train on the whole data set
Given that OOB error gives us a good way to estimate model accuracy, we can train random forest models on the entire data set, without using a train/test split (Breiman, 2001, p. 8).
set.seed(4567)
rwforFull <- randomForest(grade ~ ., data = redwineClass)
print(rwforFull)
Call:
randomForest(formula = grade ~ ., data = redwineClass)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 16.82%
Confusion matrix:
bad good class.error
bad 615 129 0.1733871
good 140 715 0.1637427
Caveat: If you plan to “tune” your model by adjusting the optional parameters in randomForest, it is still good practice to set aside a testing set for assessing model accuracy after the model has been tuned using only the training data. A train/test split is also helpful if you want to compare random forest models with other types of models.
Variable Importance
The out-of-bag errors can also be used to assess the importance of each explanatory variable in contributing to the accuracy of the model. If we set importance = TRUE in a call to randomForest, the function will keep track of how much the OOB accuracy decreases when each variable is randomly permuted. Scrambling a variable in this way effectively removes its predictive power from the model, so we would expect the most important variables to have the greatest decreases in accuracy.
set.seed(2345)
rwforFull <- randomForest(grade ~ ., data = redwineClass, importance = TRUE)
importance(rwforFull, type = 1)
MeanDecreaseAccuracy
fixed.acidity 33.60865
volatile.acidity 50.37700
citric.acid 30.12944
residual.sugar 31.40780
chlorides 34.39463
free.sulfur.dioxide 32.60753
total.sulfur.dioxide 50.95265
density 42.35901
pH 36.46366
sulphates 58.41187
alcohol 75.06260
Challenge: Most and Least Important
Based on the Mean Decrease in Accuracy, Which two variables are the most important, and which two are the least important? Are these results consistent with the decision tree model you constructed in the first challence of this episode?
Solution
For convenience, let’s sort the rows of the importance matrix.
importance(rwforFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(MeanDecreaseAccuracy))# A tibble: 11 × 2 Variable MeanDecreaseAccuracy <chr> <dbl> 1 alcohol 75.1 2 sulphates 58.4 3 total.sulfur.dioxide 51.0 4 volatile.acidity 50.4 5 density 42.4 6 pH 36.5 7 chlorides 34.4 8 fixed.acidity 33.6 9 free.sulfur.dioxide 32.6 10 residual.sugar 31.4 11 citric.acid 30.1The top two variables are
alcoholandsulphates, which both occur near the root of the decision tree. The least important variables areresidual.sugarandcitric.acid, which do not occur in the decision tree. So it seems consistent that the important variables play important roles in the decision tree, while the unimportant variables do not.
Red Wine Regression Model
So far, we have applied decision trees and random forests to classification problems, where the dependent variable is categorical. These techniques also apply to regression problems, where we are predicting a quantitative variable.
Recall that in the original wine data set, there is a variable called quality that assigns each sample a numerical quality score. For the examples that follow, we will treat quality as a quantitative variable. As before, we select the rows that contain observations of red wines, and we form training and testing sets.
redwine <- wine %>% slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% slice(trainIndex)
testDF <- redwine %>% slice(-trainIndex)
Fit a Decision Tree
When the dependent variable is quantitative, we use the method = "anova" option in rpart to construct a decision tree. In this situation, the predicted value corresponding to each node is the mean value of the observations assigned to the node, and the algorithm searches for a split that minimizes the sum of the squared errors of these predictions.
rwtree <- rpart(quality ~ ., data = trainDF, method = "anova")
rpart.plot(rwtree)
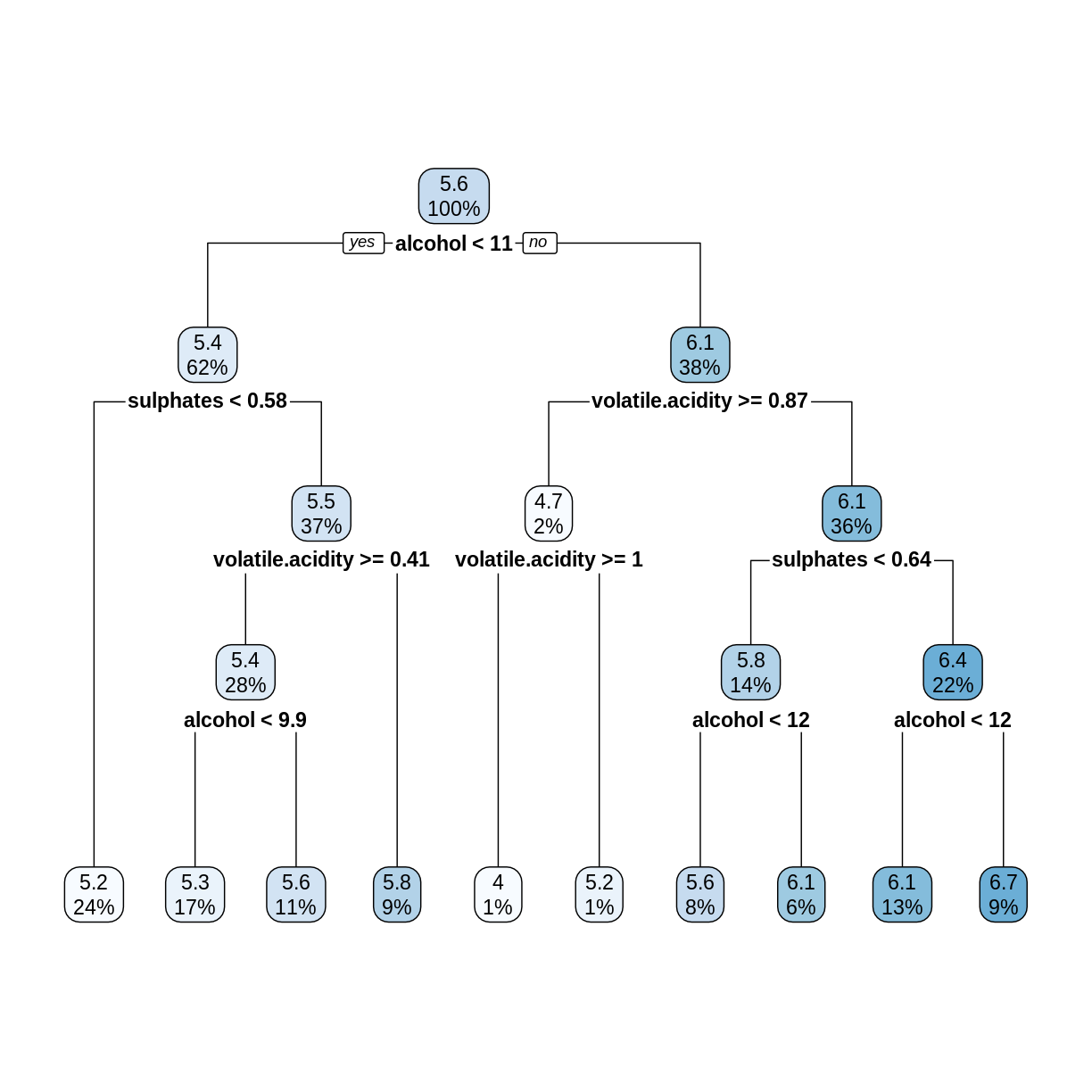
The rpart.plot command rounds off numerical values to save space. To see more digits of accuracy, print the tree in text format.
rwtree
n= 1279
node), split, n, deviance, yval
* denotes terminal node
1) root 1279 827.94210 5.636435
2) alcohol< 10.525 787 332.33800 5.364676
4) sulphates< 0.575 310 100.56770 5.154839 *
5) sulphates>=0.575 477 209.24950 5.501048
10) volatile.acidity>=0.405 364 149.63460 5.403846
20) alcohol< 9.85 223 66.76233 5.278027 *
21) alcohol>=9.85 141 73.75887 5.602837 *
11) volatile.acidity< 0.405 113 45.09735 5.814159 *
3) alcohol>=10.525 492 344.51020 6.071138
6) volatile.acidity>=0.8725 26 23.11538 4.730769
12) volatile.acidity>=1.015 10 6.00000 4.000000 *
13) volatile.acidity< 1.015 16 8.43750 5.187500 *
7) volatile.acidity< 0.8725 466 272.07730 6.145923
14) sulphates< 0.635 184 95.77717 5.831522
28) alcohol< 11.65 102 53.84314 5.627451 *
29) alcohol>=11.65 82 32.40244 6.085366 *
15) sulphates>=0.635 282 146.24470 6.351064
30) alcohol< 11.55 166 79.81325 6.138554 *
31) alcohol>=11.55 116 48.20690 6.655172 *
For example, the first split tests whether alcohol < 10.525, not 11 as shown in the plot of the tree.
Challenge: Check the Splits
In the above decision tree, consider the root (5.6), its left child (5.4), and the leftmost leaf (5.2). Check that these numbers are in fact the average
qualityvalues (rounded to one decimal place) of the observations intrainDFthat are assigned to each node.Solution
The root node contains all the observations, so compute its mean
qualityvalue.mean(trainDF$quality)[1] 5.636435The left child of the root contains observations where
alcoholis less than 10.525.trainDF %>% filter(alcohol < 10.525) %>% summarize(nodeValue = mean(quality))# A tibble: 1 × 1 nodeValue <dbl> 1 5.36The leftmost leaf contains observations where
alcoholis less than 10.525 andsulphatesis less than 0.575.trainDF %>% filter(alcohol < 10.525, sulphates < 0.575) %>% summarize(nodeValue = mean(quality))# A tibble: 1 × 1 nodeValue <dbl> 1 5.15
Decision Tree RMSE
For regression trees, each leaf is assigned a predicted value, and the predict function selects the appropriate leaf/prediction based on the values of the explanatory variables.
predictedQuality <- predict(rwtree, testDF)
head(predictedQuality)
1 2 3 4 5 6
5.154839 5.278027 5.278027 5.154839 5.154839 5.602837
Since this is a regression model, we assess its performance using the root mean squared error (RMSE).
errors <- predictedQuality - testDF$quality
decTreeRMSE <- sqrt(mean(errors^2))
decTreeRMSE
[1] 0.6862169
Random Forest Regression Model
Constructing a random forest regression model uses randomForest with the same syntax as we used for classification models. The only difference is that the response variable quality in our formula is a quantitative variable. The predicted values given by predict are the average predictions of all the trees in the forest.
set.seed(4567)
rwfor <- randomForest(quality ~ ., data = trainDF)
predQualRF <- predict(rwfor, testDF)
rfErrors <- predQualRF - testDF$quality
rfRMSE <- sqrt(mean(rfErrors^2))
rfRMSE
[1] 0.5913485
The random forest RMSE is better (smaller) than the decision tree RMSE.
print(rwfor)
Call:
randomForest(formula = quality ~ ., data = trainDF)
Type of random forest: regression
Number of trees: 500
No. of variables tried at each split: 3
Mean of squared residuals: 0.3269279
% Var explained: 49.5
The Mean of squared residuals is the MSE of the out-of-bag errors. The % Var explained term is a “pseudo R-squared”, computed as 1 - MSE/Var(y). The OOB MSE should be close to the MSE on the testing set. So again, you don’t always need a train/test split when working with random forests.
We conclude this episode with a series of challenges.
Challenge: Variable Importance
As with classification models, setting
importance = TRUEin a call torandomForestwill use the OOB errors to measure variable importance. In the regression case, the decrease in performance when a variable is permuted is measured by the percentage increase in MSE (%IncMSE). The larger the%IncMSE, the more important the variable.Compute the
%IncMSEvariable importance for the red wine regression model, and sort the variables by their importance. Re-train the model on the entireredwinedata set instead of on the testing set. Are the most important variables the same as in the classification model?Solution
The syntax is almost identical to the classification case. Since the identifier
%IncMSEcontains special characters, it must be enclosed in backticks.set.seed(2345) rwFull <- randomForest(quality ~ ., data = redwine, importance = TRUE) importance(rwFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(`%IncMSE`))# A tibble: 11 × 2 Variable `%IncMSE` <chr> <dbl> 1 alcohol 59.2 2 sulphates 55.6 3 volatile.acidity 39.7 4 total.sulfur.dioxide 38.3 5 density 34.5 6 chlorides 32.7 7 free.sulfur.dioxide 30.0 8 citric.acid 28.9 9 fixed.acidity 28.4 10 pH 25.1 11 residual.sugar 24.2The top five most important variables are the same as in the classification model, but their order is slightly different. The variable
pHseems to be relatively more important in the classification model.
Challenge: Linear Regression Model
In Episode 2, we used the
lmfunction to fit a linear model to the training set, and then we computed the RMSE on the testing set. Repeat this process for theredwinedata set. How does the linear regression RMSE compare to the random forest RMSE? Compare thesummaryof your linear model with the variable importance rankings from the previous challenge.Solution
redwine.lm <- lm(quality ~ ., data = trainDF) lmRMSE <- sqrt(mean((predict(redwine.lm, testDF) - testDF$quality)^2)) lmRMSE[1] 0.6880957The random forest RMSE is less than the linear model RMSE.
summary(redwine.lm)Call: lm(formula = quality ~ ., data = trainDF) Residuals: Min 1Q Median 3Q Max -2.68737 -0.36035 -0.03507 0.43456 1.95898 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.3242378 23.4596015 0.397 0.6911 fixed.acidity 0.0108114 0.0284758 0.380 0.7043 volatile.acidity -1.2144573 0.1320387 -9.198 < 2e-16 *** citric.acid -0.2957551 0.1608745 -1.838 0.0662 . residual.sugar 0.0193480 0.0168430 1.149 0.2509 chlorides -1.8858347 0.4583915 -4.114 4.14e-05 *** free.sulfur.dioxide 0.0054883 0.0023783 2.308 0.0212 * total.sulfur.dioxide -0.0034664 0.0007974 -4.347 1.49e-05 *** density -5.0636470 23.9244350 -0.212 0.8324 pH -0.4331191 0.2065623 -2.097 0.0362 * sulphates 0.9244109 0.1306583 7.075 2.47e-12 *** alcohol 0.2886439 0.0293633 9.830 < 2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.6385 on 1267 degrees of freedom Multiple R-squared: 0.3762, Adjusted R-squared: 0.3708 F-statistic: 69.46 on 11 and 1267 DF, p-value: < 2.2e-16The variables the smallest p-values (
Pr(>|t|)) tend to correspond to the most important variables in the random forest model.
Challenge: White Wine
Rows 1600-6497 of the
winedata frame correspond to white wine observations. Use these rows to train and test a random forest model, as we did with the red wine observations. Compute a testing set RMSE, and assess variable importance. Are the important variables for predicting white wine quality the same as the important variables for predicting red wine quality?Solution
whitewine <- wine %>% slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) wwfor <- randomForest(quality ~ ., data = trainDF) predQualww <- predict(wwfor, testDF) errors <- predQualww - testDF$quality wwRMSE <- sqrt(mean(errors^2))The RMSE on the white wine testing set is about 0.63.
set.seed(4567) wwforFull <- randomForest(quality ~ ., data = whitewine, importance = TRUE) importance(wwforFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(`%IncMSE`))Relative to red wine,
free.sulfur.dioxideis much more important for predicting white wine quality, andsulphatesis less important.
Key Points
Random forests can make predictions of a categorical or quantitative variable.
Random forests, with their default settings, work reasonably well.
Gradient Boosted Trees
Overview
Teaching: 45 min
Exercises: 25 minQuestions
What is gradient boosting?
How can we train an XGBoost model?
What is the learning rate?
Objectives
Introduce XGBoost models.
Train regression models using XGBoost
Explore the effect of learning rate on the training process.
Gradient Boosted Trees
A random forest is called an ensemble method, because it combines the results of a set of trees to form a single prediction. Gradient boosted trees are also ensemble methods, but instead of forming a forest of trees from different random samples, they grow successive trees that systematically reduce the error of the model at each iteration.
We will be using the R package xgboost, which gives a fast, scalable implementation of a gradient boosting framework. For more information on how xgboost works, see the XGBoost Presentation vignette and the Introduction to Boosted Trees tutorial in the XGBoost documentation. In this episode we will use XGBoost to create a regression model, but this framework can also be used for classification problems.
Reload the Red Wine Data
library(tidyverse)
library(here)
library(xgboost)
Attaching package: 'xgboost'
The following object is masked from 'package:dplyr':
slice
Notice that both xgboost and dplyr have a function called slice. In the following code block, we specify that we want to use the dplyr version.
wine <- read_csv(here("data", "wine.csv"))
redwine <- wine %>% dplyr::slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% dplyr::slice(trainIndex)
testDF <- redwine %>% dplyr::slice(-trainIndex)
The xgboost package defines a data structure called xgb.DMatrix that optimizes storage and retrieval. To use the advanced features of xgboost, it is necessary to convert our training and test sets to the xgb.DMatrix class.
dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality)
dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)
Training an XGBoost Model
Since we specified a label in our dtrain and dtest matrices, there is no need to specify a formula when training a model using xgb.train. The label that we specified (quality rating) will be the response variable, and the columns of the data that we specified will be the explanatory variables. One option that we must specify is nrounds, which restricts the number of boosting iterations the algorithm will make.
redwineXGB <- xgb.train(data = dtrain, nrounds = 10)
Let’s calculate the RMSE on our testing set. The predict function for XGBoost models expects a matrix, so we pass it the xgb.DMatrix that we created from our testing set.
pQuality <- predict(redwineXGB, dtest)
errors <- pQuality - testDF$quality
sqrt(mean(errors^2)) #RMSE
[1] 0.6653935
More Details on the Training Process
The xgb.train command will automatically calculate the RMSE on our testing set after each iteration if we set the testing set in the watchlist.
redwineXGB <- xgb.train(data = dtrain, watchlist = list(test = dtest), nrounds = 10)
[1] test-rmse:3.676492
[2] test-rmse:2.620643
[3] test-rmse:1.904736
[4] test-rmse:1.414777
[5] test-rmse:1.110905
[6] test-rmse:0.913236
[7] test-rmse:0.793578
[8] test-rmse:0.729415
[9] test-rmse:0.686777
[10] test-rmse:0.665393
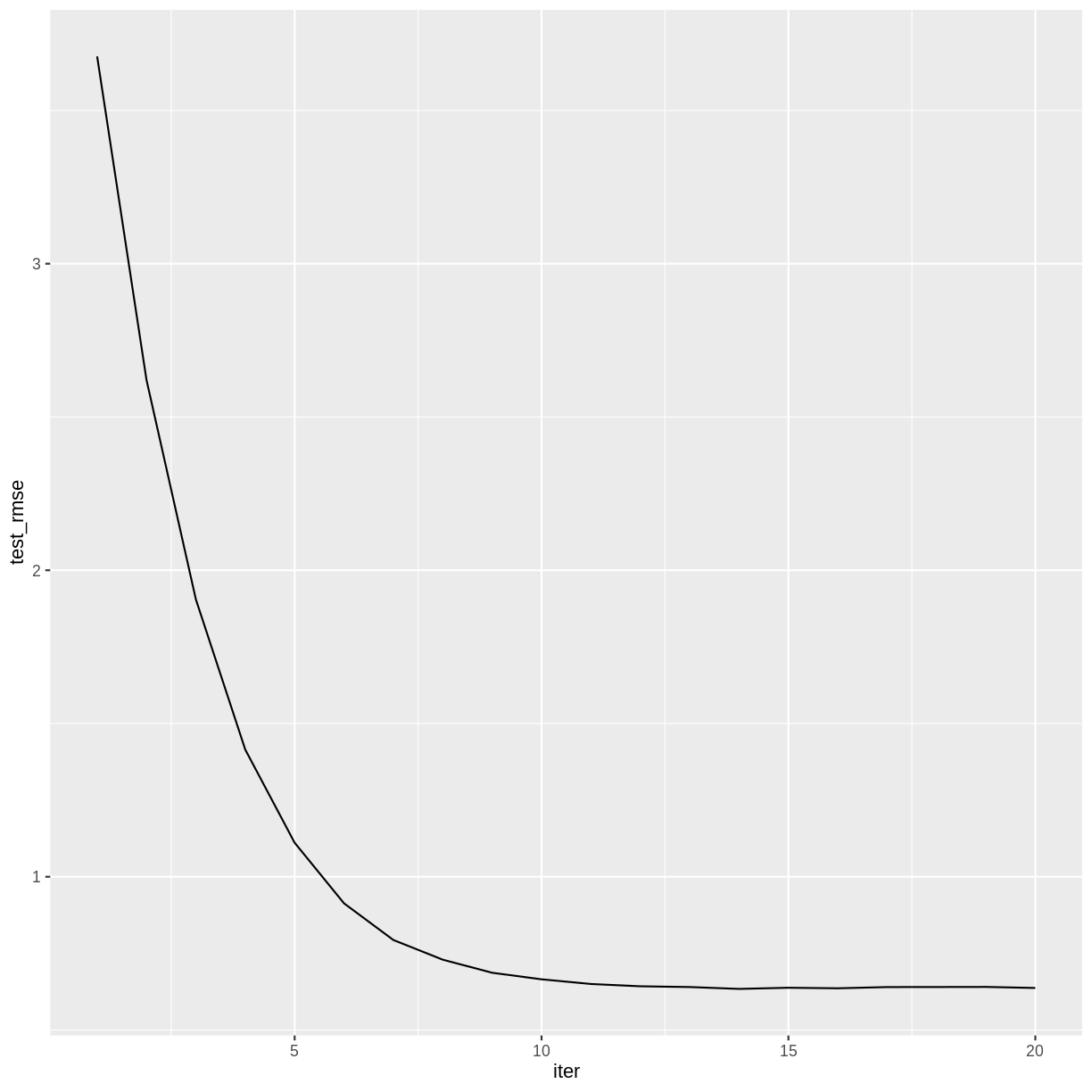
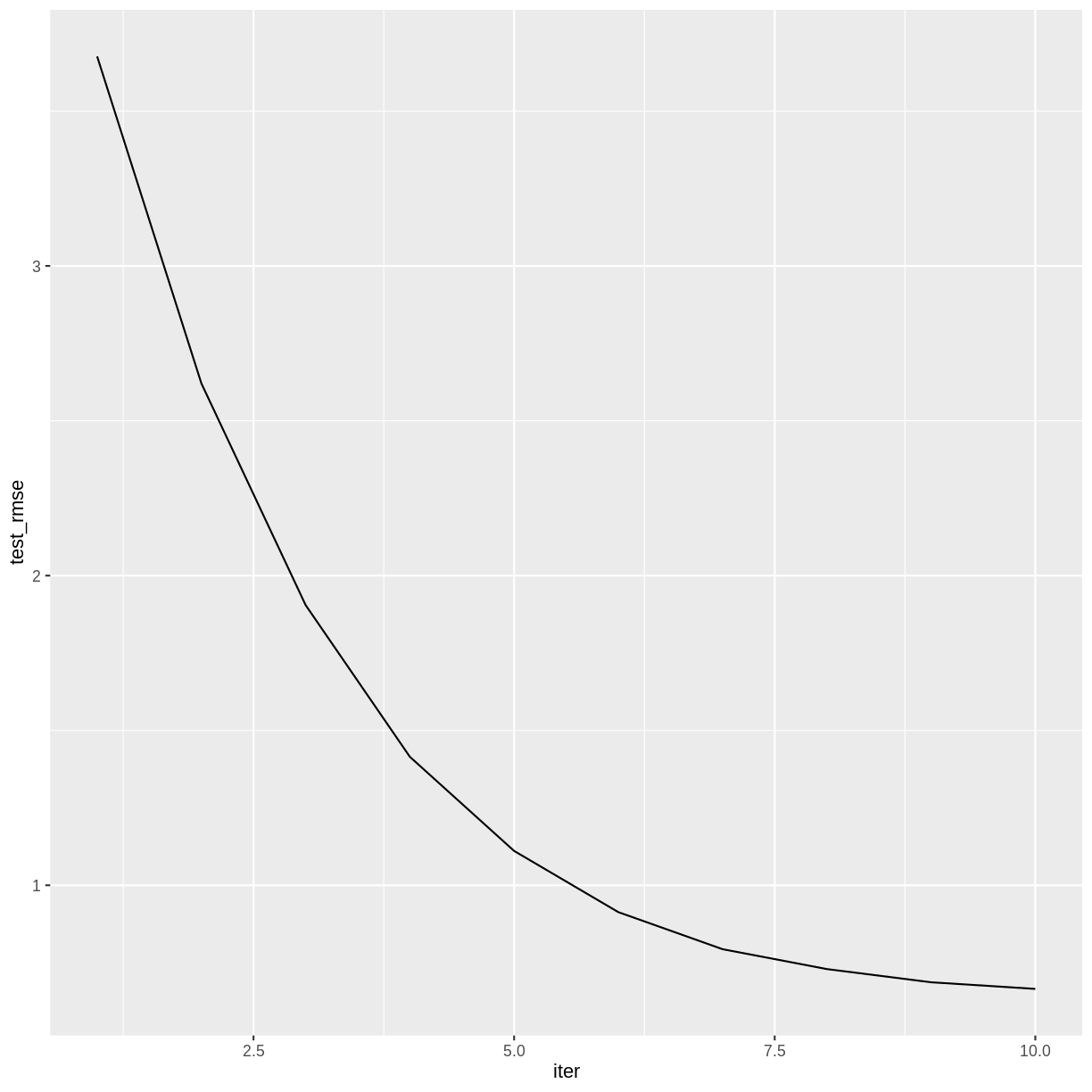
The training history is saved as a data frame in the variable gbm$evaluation_log, so we can plot how the RMSE changes during the training process.
redwineXGB$evaluation_log %>%
ggplot(aes(x = iter, y = test_rmse)) +
geom_line()
Challenge: How many boosting iterations?
Experiment with different values of
nroundsin the above call toxgb.train. Does the accuracy of the model improve with more iterations? Is there a point after which the model ceases to improve?Solution
The accuracy of the model doesn’t appear to improve after iteration 14.
redwineXGB <- xgb.train(data = dtrain, watchlist = list(test = dtest), nrounds = 20)[1] test-rmse:3.676492 [2] test-rmse:2.620643 [3] test-rmse:1.904736 [4] test-rmse:1.414777 [5] test-rmse:1.110905 [6] test-rmse:0.913236 [7] test-rmse:0.793578 [8] test-rmse:0.729415 [9] test-rmse:0.686777 [10] test-rmse:0.665393 [11] test-rmse:0.650133 [12] test-rmse:0.642655 [13] test-rmse:0.640231 [14] test-rmse:0.634134 [15] test-rmse:0.637910 [16] test-rmse:0.636140 [17] test-rmse:0.640103 [18] test-rmse:0.640305 [19] test-rmse:0.640569 [20] test-rmse:0.637183redwineXGB$evaluation_log %>% ggplot(aes(x = iter, y = test_rmse)) + geom_line()
Learning Rate
Machine learning algorithms that reduce a loss function over a sequence of iterations typically have a setting that controls the learning rate. A smaller learning rate will generally reduce the error by a smaller amount at each iteration, and therefore will require more iterations to arrive at a given level of accuracy. The advantage to a smaller learning rate is that the algorithm is less likely to overshoot the optimum fit.
In XGBoost, the setting that controls the learning rate is called eta, which is one of several hyperparameters that can be adjusted. Its default value is 0.3, but smaller values will usually perform better. It must take a value in the range 0 < eta < 1.
The following code will set eta to its default value. We include a value for early_stopping_rounds, which will halt the training after a specified number of iterations pass without improvement. When using early_stopping_rounds, nrounds can be set to a very large number. To avoid printing too many lines of output, we also set a value for print_every_n.
redwineXGB <- xgb.train(data = dtrain,
params = list(eta = 0.3),
watchlist = list(test = dtest),
nrounds = 1000,
early_stopping_rounds = 10,
print_every_n = 5)
[1] test-rmse:3.676492
Will train until test_rmse hasn't improved in 10 rounds.
[6] test-rmse:0.913236
[11] test-rmse:0.650133
[16] test-rmse:0.636140
[21] test-rmse:0.639540
Stopping. Best iteration:
[14] test-rmse:0.634134
The 14th iteration had the smallest RMSE, as we found in the previous challenge.
Challenge: Experiment with the learning rate.
Experiment with different values of
etain the above call toxgb.train. Notice how smaller values of eta require more iterations. Can you find a value ofetathat results in a lower testing set RMSE than the default?Solution
A learning rate around 0.1 reduces the RMSE somewhat.
redwineXGB <- xgb.train(data = dtrain, params = list(eta = 0.1), watchlist = list(test = dtest), nrounds = 1000, early_stopping_rounds = 10, print_every_n = 15)[1] test-rmse:4.689984 Will train until test_rmse hasn't improved in 10 rounds. [16] test-rmse:1.164598 [31] test-rmse:0.655252 [46] test-rmse:0.618707 [61] test-rmse:0.617009 [76] test-rmse:0.612820 Stopping. Best iteration: [75] test-rmse:0.612406
Variable Importance
As with random forests, you can view the predictive importance of each explanatory variable.
xgb.importance(model = redwineXGB)
Feature Gain Cover Frequency
1: alcohol 0.33236129 0.11264259 0.07936508
2: volatile.acidity 0.12367170 0.09820458 0.11922399
3: sulphates 0.10975935 0.10726694 0.08218695
4: total.sulfur.dioxide 0.07500529 0.13655797 0.09276896
5: density 0.05960668 0.09451465 0.08500882
6: chlorides 0.05883225 0.10318293 0.09805996
7: residual.sugar 0.05499778 0.09106117 0.08818342
8: fixed.acidity 0.05087633 0.07920964 0.14250441
9: pH 0.04772447 0.06078573 0.06807760
10: citric.acid 0.04532904 0.07698668 0.07830688
11: free.sulfur.dioxide 0.04183582 0.03958713 0.06631393
The rows are sorted by Gain, which measures the accuracy improvement contributed by a feature based on all the splits it determines. Note that the sum of all the gains is 1.
Training Error vs. Testing Error
Like many machine learning algorithms, gradient boosting operates by minimizing the error on the training set. However, we evaluate its performance by computing the error on the testing set. These two errors are usually different, and it is not uncommon to have much lower training RMSE than testing RMSE.
To see both training and testing errors, we can add a train item to the watchlist.
redwineXGB <- xgb.train(data = dtrain,
params = list(eta = 0.1),
watchlist = list(train = dtrain, test = dtest),
nrounds = 1000,
early_stopping_rounds = 10,
print_every_n = 15)
[1] train-rmse:4.690120 test-rmse:4.689984
Multiple eval metrics are present. Will use test_rmse for early stopping.
Will train until test_rmse hasn't improved in 10 rounds.
[16] train-rmse:1.109302 test-rmse:1.164598
[31] train-rmse:0.467275 test-rmse:0.655252
[46] train-rmse:0.369513 test-rmse:0.618707
[61] train-rmse:0.328256 test-rmse:0.617009
[76] train-rmse:0.290210 test-rmse:0.612820
Stopping. Best iteration:
[75] train-rmse:0.291627 test-rmse:0.612406
redwineXGB$evaluation_log %>%
pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>%
ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()
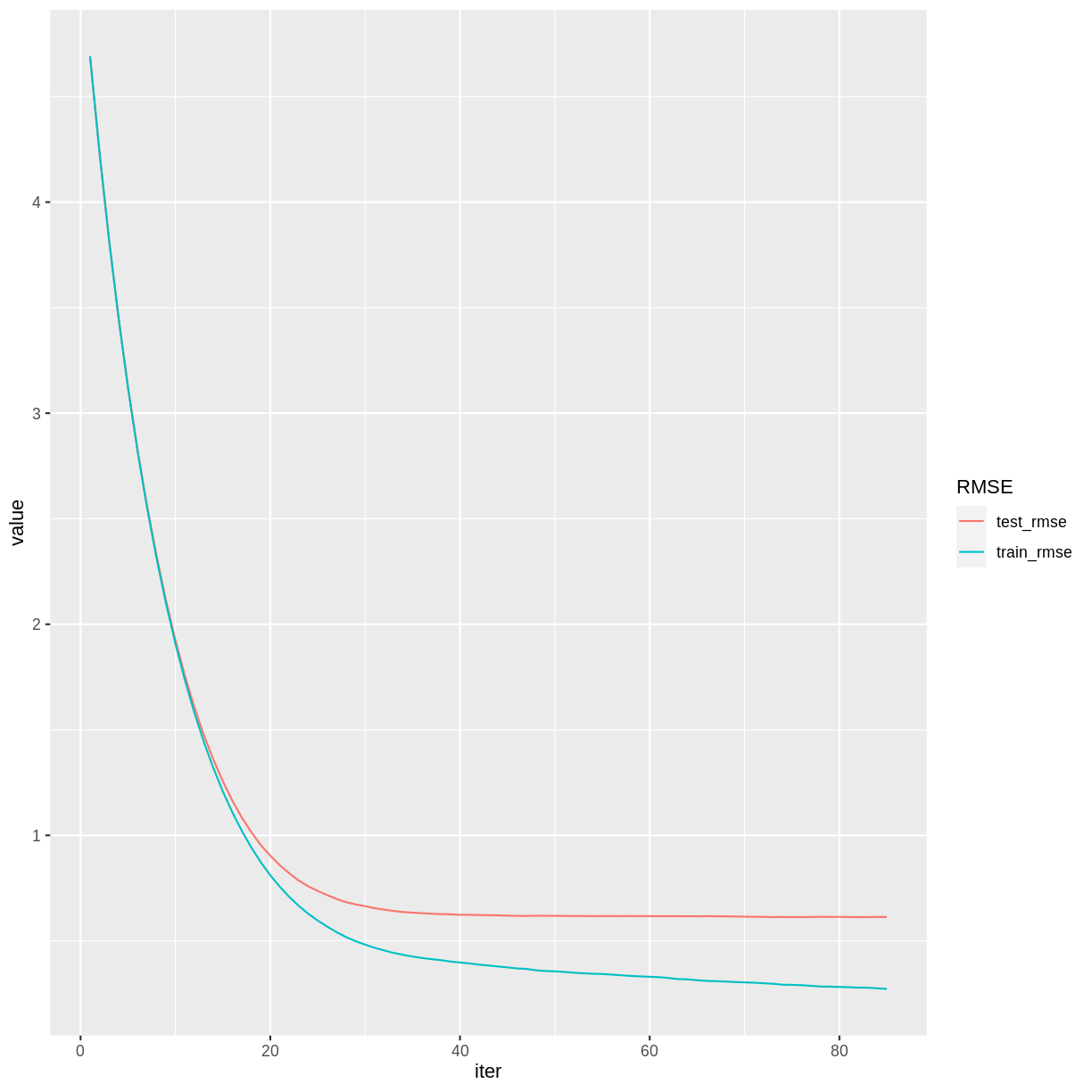
Notice that beyond iteration 40 or so, the training RMSE continues to decrease while the testing RMSE has basically stabilized. This divergence indicates that the later training iterations are improving the model based on the particularities of the training set, but in a way that does not generalize to the testing set.
Saving a trained model
As models become more complicated, the time it takes to train them becomes nontrivial. For this reason, it can be helpful to save a trained XGBoost model. We’ll create a directory in our project called saved_models and save our XGBoost model in a universal binary format that can be read by any XGBoost interface (e.g., R, Python, Julia, Scala).
dir.create(here("saved_models"))
xgb.save(redwineXGB, here("saved_models", "redwine.model"))
This trained model can be loaded into a future R session with the xgb.load command.
reloaded_model <- xgb.load(here("saved_models", "redwine.model"))
However, while reloaded_model can be used with the predict function, it is not identical to the redwineXGB object. For reproducibility, it is important to save the source code used in the training process.
Challenge: White Wine
Build an XGBoost model for the white wine data (rows 1600-6497) of the
winedata frame. Compare the RMSE and variable importance with the random forest white wine model from the previous episode.Solution
whitewine <- wine %>% dplyr::slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality) dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality) whitewineXGB <- xgb.train(data = dtrain, params = list(eta = 0.1), watchlist = list(train = dtrain, test = dtest), nrounds = 1000, early_stopping_rounds = 10, print_every_n = 20) xgb.importance(model = whitewineXGB) whitewineXGB$evaluation_log %>% pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>% ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()The testing set RMSE (0.664) is worse than what we obtained in the random forest model (0.63). The important explanatory variables are similar.
So far, our XGBoost models have performed slightly worse than the equivalent random forest models. In the next episode we will explore ways to improve these results.
Key Points
Gradient boosted trees can be used for the same types of problems that random forests can solve.
The learning rate can affect the performance of a machine learning algorithm.
Cross Validation and Tuning
Overview
Teaching: 45 min
Exercises: 30 minQuestions
How can the fit of an XGBoost model be improved?
What is cross validation?
What are some guidelines for tuning parameters in a machine learning algorithm?
Objectives
Explore the effects of adjusting the XGBoost parameters.
Practice some coding techniques to tune parameters using grid searching and cross validation.
Parameter Tuning
Like many other machine learning algorithms, XGBoost has an assortment of parameters that control the behavior of the training process. (These parameters are sometimes referred to as hyperparameters, because they cannot be directly estimated from the data.) To improve the fit of the model, we can adjust, or tune, these parameters. According to the notes on parameter tuning in the XGBoost documentation, “[p]arameter tuning is a dark art in machine learning,” so it is difficult to prescribe an automated process for doing so. In this episode we will develop some coding practices for tuning an XGBoost model, but be advised that the optimal way to tune a model will depend heavily on the given data set.
You can find a complete list of XGBoost parameters in the documentation. Generally speaking, each parameter controls the complexity of the model in some way. More complex models tend to fit the training data more closely, but such models can be very sensitive to small changes in the training set. On the other hand, while less complex models can be more conservative in this respect, they have a harder time modeling intricate relationships. The “art” of parameter tuning lies in finding an appropriately complex model for the problem at hand.
A complete discussion of the issues involved are beyond the scope of this lesson. An excellent resource on the topic is An Introduction to Statistical Learning, by James, Witten, Hastie, and Tibshirani. In particular, Section 2.2.2 discusses the Bias-Variance Trade-Off inherent in statistical learning methods.
Cross Validation
How will we be able to tell if an adjustment to a parameter has improved the model? One possible approach would be to test the model before and after the adjustment on the testing set. However, the problem with this method is that it runs the risk of tuning the model to the particular properties of the testing set, rather than to general future cases that we might encounter. It is better practice to save our testing set until the very end of the process, and then use it to test the accuracy of our model. Training set accuracy, as we have seen, tends to underestimate the accuracy of a machine learning model, so tuning to the training set may also fail to make improvements that generalize.
An alternative testing procedure is to use cross validation on the training set to judge the effect of tuning adjustments. In k-fold cross validation, the training set is partitioned randomly into k subsets. Each of these subsets takes a turn as a testing set, while the model is trained on the remaining data. The accuracy of the model is then measured k times, and the results are averaged to obtain an estimate of the overall model performance. In this way we can be more certain that repeated adjustments will be tested in ways that generalize to future observations. It also allows us to save the original testing set for a final test of our tuned model.
Revisit the Red Wine Quality Model
Let’s see if we can improve the previous episode’s model for predicting red wine quality.
library(tidyverse)
library(here)
library(xgboost)
wine <- read_csv(here("data", "wine.csv"))
redwine <- wine %>% dplyr::slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% dplyr::slice(trainIndex)
testDF <- redwine %>% dplyr::slice(-trainIndex)
dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality)
dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)
The xgb.cv command handles most of the details of the cross validation process. Since this is a random process, we will set a seed value for reproducibility. We will use 10 folds and the default value of 0.3 for eta.
set.seed(524)
rwCV <- xgb.cv(params = list(eta = 0.3),
data = dtrain,
nfold = 10,
nrounds = 500,
early_stopping_rounds = 10,
print_every_n = 5)
[1] train-rmse:3.676824+0.003733 test-rmse:3.682796+0.044551
Multiple eval metrics are present. Will use test_rmse for early stopping.
Will train until test_rmse hasn't improved in 10 rounds.
[6] train-rmse:0.808822+0.003848 test-rmse:0.888110+0.043011
[11] train-rmse:0.418891+0.013364 test-rmse:0.641062+0.037335
[16] train-rmse:0.343756+0.012450 test-rmse:0.628046+0.033493
[21] train-rmse:0.299929+0.010728 test-rmse:0.625757+0.033106
[26] train-rmse:0.258271+0.013402 test-rmse:0.624861+0.036458
[31] train-rmse:0.225188+0.013268 test-rmse:0.623947+0.042251
[36] train-rmse:0.194026+0.011849 test-rmse:0.624094+0.042001
Stopping. Best iteration:
[29] train-rmse:0.236075+0.013368 test-rmse:0.622687+0.041345
The output appears similar to the xgb.train command. Notice that each error estimate now includes a standard deviation, because these estimates are formed by averaging over all ten folds. The function returns a list, which we have given the name rwCV. Its names hint at what each list item represents.
names(rwCV)
[1] "call" "params" "callbacks" "evaluation_log"
[5] "niter" "nfeatures" "folds" "best_iteration"
[9] "best_ntreelimit"
Challenge: Examine the cross validation results
- Examine the list item
rwCV$folds. What do suppose these numbers represent? Are all the folds the same size? Can you explain why/why not?- Display the evaluation log with rows sorted by
test_rmse_mean.- How could you display only the row containing the best iteration?
Solution
- The numbers are the indexes of the rows in each fold. The folds are not all the same size, because no row can be used more than once, and there are 1279 rows total in the training set, so they don’t divide evenly into 10 partitions.
rwCV$evaluation_log %>% arrange(test_rmse_mean)iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std 1: 29 0.2360750 0.013368348 0.6226874 0.04134490 2: 35 0.2007999 0.011608484 0.6229431 0.04233848 3: 33 0.2134821 0.012373642 0.6229542 0.04233916 4: 32 0.2192703 0.013306955 0.6229588 0.04129835 5: 34 0.2076733 0.012222030 0.6233336 0.04166854 6: 28 0.2426037 0.013287443 0.6233426 0.03899304 7: 31 0.2251878 0.013267807 0.6239475 0.04225134 8: 36 0.1940258 0.011849455 0.6240940 0.04200144 9: 30 0.2310984 0.012281978 0.6241792 0.04091916 10: 27 0.2507866 0.013086816 0.6241843 0.03830991 11: 37 0.1893309 0.011079029 0.6243738 0.04193406 12: 25 0.2659939 0.012269906 0.6245430 0.03553351 13: 39 0.1790856 0.011285008 0.6245503 0.04176559 14: 38 0.1846427 0.010905405 0.6247798 0.04141676 15: 26 0.2582708 0.013402250 0.6248607 0.03645813 16: 23 0.2835744 0.010293100 0.6256707 0.03261529 17: 21 0.2999289 0.010728491 0.6257569 0.03310647 18: 18 0.3203636 0.010830155 0.6257911 0.03230540 19: 22 0.2910245 0.011284146 0.6259865 0.03283513 20: 24 0.2760180 0.012458570 0.6260504 0.03340596 21: 20 0.3067600 0.010738381 0.6262777 0.03185302 22: 17 0.3320214 0.011822742 0.6271510 0.03445198 23: 19 0.3119272 0.010392821 0.6272786 0.03191304 24: 15 0.3564079 0.012468678 0.6273193 0.03434991 25: 16 0.3437564 0.012450158 0.6280460 0.03349317 26: 14 0.3679581 0.011806629 0.6285073 0.03311778 27: 13 0.3802030 0.011004878 0.6307059 0.03545827 28: 12 0.3983362 0.010466897 0.6353593 0.03506220 29: 11 0.4188905 0.013364106 0.6410624 0.03733492 30: 10 0.4497433 0.011540044 0.6501031 0.04014740 31: 9 0.4915645 0.010805274 0.6679334 0.03942590 32: 8 0.5556933 0.007217608 0.7061343 0.03954675 33: 7 0.6565486 0.004032585 0.7713876 0.04152207 34: 6 0.8088225 0.003847863 0.8881101 0.04301120 35: 5 1.0398669 0.003228572 1.0914671 0.04090907 36: 4 1.3825695 0.002820641 1.4113087 0.03738249 37: 3 1.8857284 0.002530300 1.9004059 0.04118868 38: 2 2.6184095 0.002917347 2.6270221 0.04337352 39: 1 3.6768236 0.003733214 3.6827955 0.04455107 iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_stdrwCV$evaluation_log[rwCV$best_iteration]iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std 1: 29 0.236075 0.01336835 0.6226874 0.0413449
Repeat Cross Validation in a Loop
To expedite the tuning process, it helps to design a loop to run repeated cross validations on different parameter values. We can start by choosing a value of eta from a list of candidate values.
paramDF <- tibble(eta = c(0.001, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4))
The following command converts a data frame to a list of lists. The split function splits paramDF into a list of its rows, and then the lapply function converts each row to a list. Each item of paramlist will be a list giving a valid parameter setting that we can use in the xgb.cv function.
paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list)
Now we will write a loop that will perform a different cross validation for each parameter setting in the paramList list. We’ll keep track of the best iterations in the bestResults tibble. To avoid too much printing, we set verbose = FALSE and use a txtProgressBar to keep track of our progress. On some systems, it may be necessary to use gc() to prevent running out of memory.
bestResults <- tibble()
set.seed(708)
pb <- txtProgressBar(style = 3)
for(i in seq(length(paramList))) {
rwCV <- xgb.cv(params = paramList[[i]],
data = dtrain,
nrounds = 500,
nfold = 10,
early_stopping_rounds = 10,
verbose = FALSE)
bestResults <- bestResults %>%
bind_rows(rwCV$evaluation_log[rwCV$best_iteration])
gc() # Free unused memory after each loop iteration
setTxtProgressBar(pb, i/length(paramList))
}
close(pb) # done with the progress bar
We now have all of the best iterations in the bestResults data frame, which we can combine with the data frame of parameter values.
etasearch <- bind_cols(paramDF, bestResults)
In RStudio, it is convenient to use View(etasearch) to view the results in a separate tab. We can use the RStudio interface to sort by mean_test_rmse.
Note that there is not much difference in mean_test_rmse among the best three choices. As we have seen in the previous episode, the choice of eta typically involves a trade-off between speed and accuracy. A common approach is to pick a reasonable value of eta and then stick with it for the rest of the tuning process. Let’s use eta = 0.1, because it uses about half as many steps as eta = 0.05, and the accuracy is comparable.
Grid Search
Sometimes it helps to tune a pair of related parameters together. A grid search runs through all possible combinations of candidate values for a selection of parameters.
We will tune the parameters max_depth and max_leaves together. These both affect the size the trees that the algorithm grows. Deeper trees with more leaves make the model more complex. We use the expand.grid function to store some reasonable candidate values in paramDF.
paramDF <- expand.grid(
max_depth = seq(15, 29, by = 2),
max_leaves = c(63, 127, 255, 511, 1023, 2047, 4095),
eta = 0.1)
If you View(paramDF) you can see that we have 56 different parameter choices to run through. The rest of the code is the same as before, but this loop might take a while to execute.
paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list)
bestResults <- tibble()
set.seed(312)
pb <- txtProgressBar(style = 3)
for(i in seq(length(paramList))) {
rwCV <- xgb.cv(params = paramList[[i]],
data = dtrain,
nrounds = 500,
nfold = 10,
early_stopping_rounds = 10,
verbose = FALSE)
bestResults <- bestResults %>%
bind_rows(rwCV$evaluation_log[rwCV$best_iteration])
gc()
setTxtProgressBar(pb, i/length(paramList))
}
close(pb)
depth_leaves <- bind_cols(paramDF, bestResults)
When we View(depth_leaves) we see that a choice of max_depth = 21 and max_leaves = 4095 results in the best test_rmse_mean. One caveat is that cross validation is a random process, so running this code with a different random seed may very well produce a different result. However, there are several comparable results with max_depth in the 20s and max_leaves in the 1000s, so we can be pretty sure that our choice these parameter values is sound.
Challenge: Write a Grid Search Function
Instead of repeatedly using the above code block, let’s package it into an R function. Define a function called
GridSearchthat consumes a data frameparamDFof candidate parameter values and anxgb.DMatrixdtrainof training data. The function should return a data frame combining the columns ofparamDFwith the corresponding results of the best cross validation iteration. The returned data frame should be sorted in ascending order oftest_rmse_mean.Solution
GridSearch <- function(paramDF, dtrain) { paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list) bestResults <- tibble() pb <- txtProgressBar(style = 3) for(i in seq(length(paramList))) { rwCV <- xgb.cv(params = paramList[[i]], data = dtrain, nrounds = 500, nfold = 10, early_stopping_rounds = 10, verbose = FALSE) bestResults <- bestResults %>% bind_rows(rwCV$evaluation_log[rwCV$best_iteration]) gc() setTxtProgressBar(pb, i/length(paramList)) } close(pb) return(bind_cols(paramDF, bestResults) %>% arrange(test_rmse_mean)) }Check the function on a small example.
set.seed(630) GridSearch(tibble(eta = c(0.3, 0.2, 0.1)), dtrain)| | | 0% | |======================= | 33% | |=============================================== | 67% | |======================================================================| 100%# A tibble: 3 × 6 eta iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 0.1 100 0.220 0.00805 0.589 0.0543 2 0.2 40 0.256 0.0123 0.598 0.0426 3 0.3 41 0.170 0.00669 0.610 0.0468
Adding Random Sampling
Adding random sampling to the training process can help make the model less dependent on the training set, and hopefully more accurate when generalizing to future cases. In XGBoost, the two parameters subsample and colsample_bytree will grow trees based on a random sample of a specified percentage of rows and columns, respectively. Typical values for these parameters are between 0.5 and 1.0 (where 1.0 implies that no random sampling will be done).
Challenge: Tune Row and Column Sampling
Use a grid search to tune the parameters
subsampleandcolsample_bytree. Choose candidate values between 0.5 and 1.0. Use our previously chosen values ofeta,max_depth, andmax_leaves.Solution
paramDF <- expand.grid( subsample = seq(0.5, 1, by = 0.1), colsample_bytree = seq(0.5, 1, by = 0.1), max_depth = 21, max_leaves = 4095, eta = 0.1) set.seed(848) randsubsets <- GridSearch(paramDF, dtrain)It appears that some amount of randomization helps, but there are many choices for
subsampleandcolsample_bytreethat seem equivalent.
Final Check using the Testing Set
Once a model has been tuned using the training set and cross validation, it can be tested using the testing set. Note that we have not used the testing set in any of our tuning experiments, so the testing set accuracy should give a fair assessment of the accuracy of our tuned model relative to the other models we have explored.
We give parameters max_depth, max_leaves, subsample, and colsample_bytree the values that we chose during the tuning process. Since we only have to do one training run, a smaller learning rate won’t incur much of a time penalty, so we set eta = 0.05.
set.seed(805)
rwMod <- xgb.train(data = dtrain, verbose = 0,
watchlist = list(train = dtrain, test = dtest),
nrounds = 10000,
early_stopping_rounds = 50,
max_depth = 21,
max_leaves = 4095,
subsample = 0.8,
colsample_bytree = 0.7,
eta = 0.05)
rwMod$evaluation_log %>%
pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>%
ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()
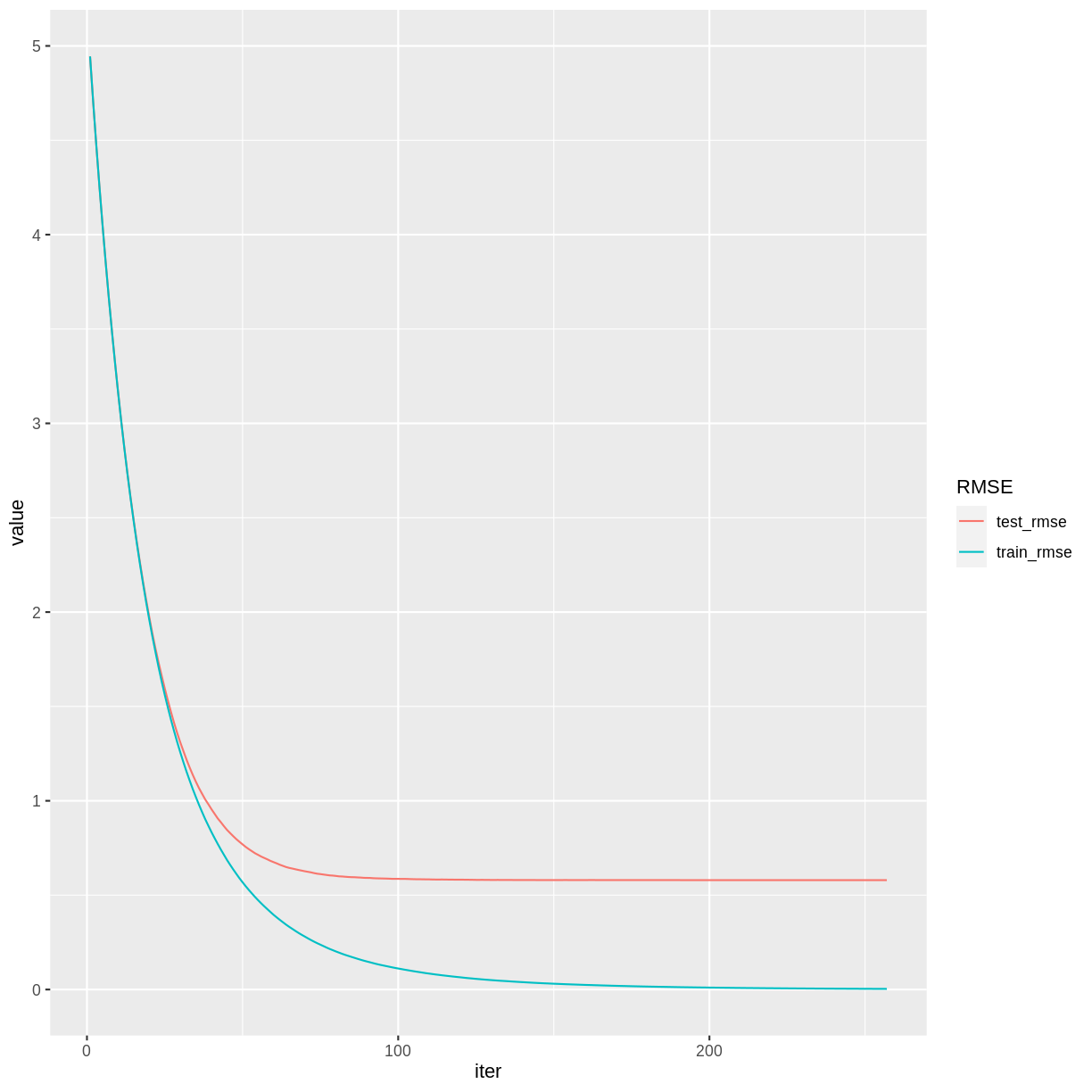
print(rwMod)
##### xgb.Booster
raw: 5.9 Mb
call:
xgb.train(data = dtrain, nrounds = 10000, watchlist = list(train = dtrain,
test = dtest), verbose = 0, early_stopping_rounds = 50, max_depth = 21,
max_leaves = 4095, subsample = 0.8, colsample_bytree = 0.7,
eta = 0.05)
params (as set within xgb.train):
max_depth = "21", max_leaves = "4095", subsample = "0.8", colsample_bytree = "0.7", eta = "0.05", validate_parameters = "1"
xgb.attributes:
best_iteration, best_msg, best_ntreelimit, best_score, niter
callbacks:
cb.evaluation.log()
cb.early.stop(stopping_rounds = early_stopping_rounds, maximize = maximize,
verbose = verbose)
# of features: 11
niter: 257
best_iteration : 207
best_ntreelimit : 207
best_score : 0.579419
best_msg : [207] train-rmse:0.008751 test-rmse:0.579419
nfeatures : 11
evaluation_log:
iter train_rmse test_rmse
1 4.944344393 4.9445344
2 4.702804815 4.7020469
---
256 0.003205872 0.5795760
257 0.003140355 0.5795782
After some tuning, our testing set RMSE is down to 0.58, which is an improvement over the previous episode, and comparable to the RMSE we obtained using the random forest model.
Challenge: Improve the White Wine Model
Improve your XGBoost model for the white wine data (rows 1600-6497) of the
winedata frame. Use grid searches to tune several parameters, using only the training set during the tuning process. Can you improve the testing set RMSE over the white wine challenges from the previous two episodes?Solution
Results may vary. The proposed solution below will take quite some time to execute.
whitewine <- wine %>% dplyr::slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality) dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)Start by tuning
max_depthandmax_leavestogether.paramGrid <- expand.grid( max_depth = seq(10, 40, by = 2), max_leaves = c(15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191), eta = 0.1 ) set.seed(1981) ww_depth_leaves <- GridSearch(paramGrid, dtrain)There are several options that perform similarly. Let’s choose
max_depth= 12 along withmax_leaves= 255. Now we tune the two random sampling parameters together.paramGrid <- expand.grid( subsample = seq(0.5, 1, by = 0.1), colsample_bytree = seq(0.5, 1, by = 0.1), max_depth = 12, max_leaves = 255, eta = 0.1 ) set.seed(867) ww_randsubsets <- GridSearch(paramGrid, dtrain)Again, some randomization seems to help, but there are several options. We’ll choose
subsample= 0.9 andcolsample_bytree= 0.6. Finally, we train the model with the chosen parameters.set.seed(5309) ww_gbmod <- xgb.train(data = dtrain, verbose = 0, watchlist = list(train = dtrain, test = dtest), nrounds = 10000, early_stopping_rounds = 50, max_depth = 12, max_leaves = 255, subsample = 0.9, colsample_bytree = 0.6, eta = 0.01)The tuned XGBoost model has a testing set RMSE of about 0.62, which is better than the un-tuned model from the last episode (0.66), and also better than the random forest model (0.63).
Key Points
Parameter tuning can improve the fit of an XGBoost model.
Cross validation allows us to tune parameters using the training set only, saving the testing set for final model evaluation.