Random Forests
Overview
Teaching: 60 min
Exercises: 30 minQuestions
What are random forests?
How do random forests improve decision tree models?
Objectives
Introduce random forests.
Use random forests for classification and regression models.
Evaluate the quality of a random forest model.
We saw in the previous episode that decision tree models can be sensitive to small changes in the training data. Random Forests mitigate this issue by forming an ensemble (i.e., set) of decision trees, and using them all together to make a prediction.
Wine Dataset
For this episode, we will use a data set described in the article Modeling wine preferences by data mining from physicochemical properties, in Decision Support Systems, 47(4):547-553, by P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis. (Instructions for downloading this data set are in the setup page.) The data set contains quality ratings and measurements from 6497 samples of wine; rows 1:1599 are red wine samples, and rows 1600:6497 are white wine.
library(tidyverse)
library(here)
wine <- read_csv(here("data", "wine.csv"))
glimpse(wine)
Rows: 6,497
Columns: 12
$ fixed.acidity <dbl> 7.4, 7.8, 7.8, 11.2, 7.4, 7.4, 7.9, 7.3, 7.8, 7.5…
$ volatile.acidity <dbl> 0.700, 0.880, 0.760, 0.280, 0.700, 0.660, 0.600, …
$ citric.acid <dbl> 0.00, 0.00, 0.04, 0.56, 0.00, 0.00, 0.06, 0.00, 0…
$ residual.sugar <dbl> 1.9, 2.6, 2.3, 1.9, 1.9, 1.8, 1.6, 1.2, 2.0, 6.1,…
$ chlorides <dbl> 0.076, 0.098, 0.092, 0.075, 0.076, 0.075, 0.069, …
$ free.sulfur.dioxide <dbl> 11, 25, 15, 17, 11, 13, 15, 15, 9, 17, 15, 17, 16…
$ total.sulfur.dioxide <dbl> 34, 67, 54, 60, 34, 40, 59, 21, 18, 102, 65, 102,…
$ density <dbl> 0.9978, 0.9968, 0.9970, 0.9980, 0.9978, 0.9978, 0…
$ pH <dbl> 3.51, 3.20, 3.26, 3.16, 3.51, 3.51, 3.30, 3.39, 3…
$ sulphates <dbl> 0.56, 0.68, 0.65, 0.58, 0.56, 0.56, 0.46, 0.47, 0…
$ alcohol <dbl> 9.4, 9.8, 9.8, 9.8, 9.4, 9.4, 9.4, 10.0, 9.5, 10.…
$ quality <dbl> 5, 5, 5, 6, 5, 5, 5, 7, 7, 5, 5, 5, 5, 5, 5, 5, 7…
ggplot(wine, aes(x = quality)) + geom_histogram(binwidth = 1)
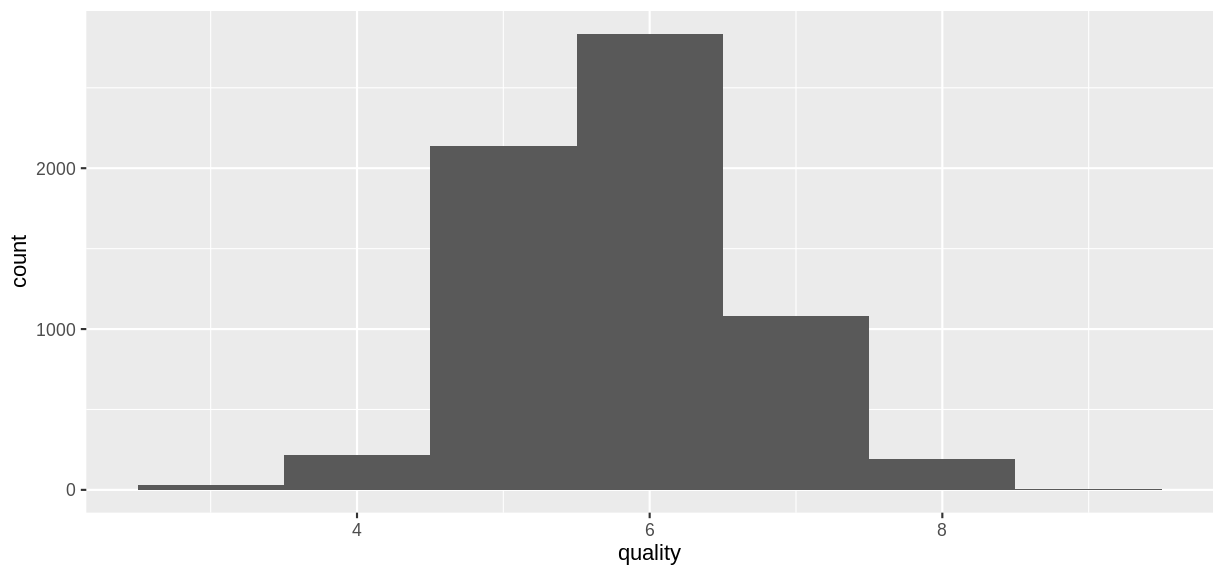The goal of the models that follow will be to predict the quality rating of a wine sample from its chemical properties.
Red Wine Classification Model
To illustrate classification models with this data set, let’s create a categorical variable grade that will serve as a response variable.
redwineClass <- wine %>%
slice(1:1599) %>% # just the red wine samples
mutate(grade = as_factor(if_else(quality < 5.5, "bad", "good"))) %>%
select(-quality) # get rid of the quality variable
summary(redwineClass$grade)
bad good
744 855
Create Training and Test Sets
Create training and test sets using an 80/20 split.
trainSize <- round(0.80 * nrow(redwineClass))
set.seed(1234)
trainIndex <- sample(nrow(redwineClass), trainSize)
trainDF <- redwineClass %>% slice(trainIndex)
testDF <- redwineClass %>% slice(-trainIndex)
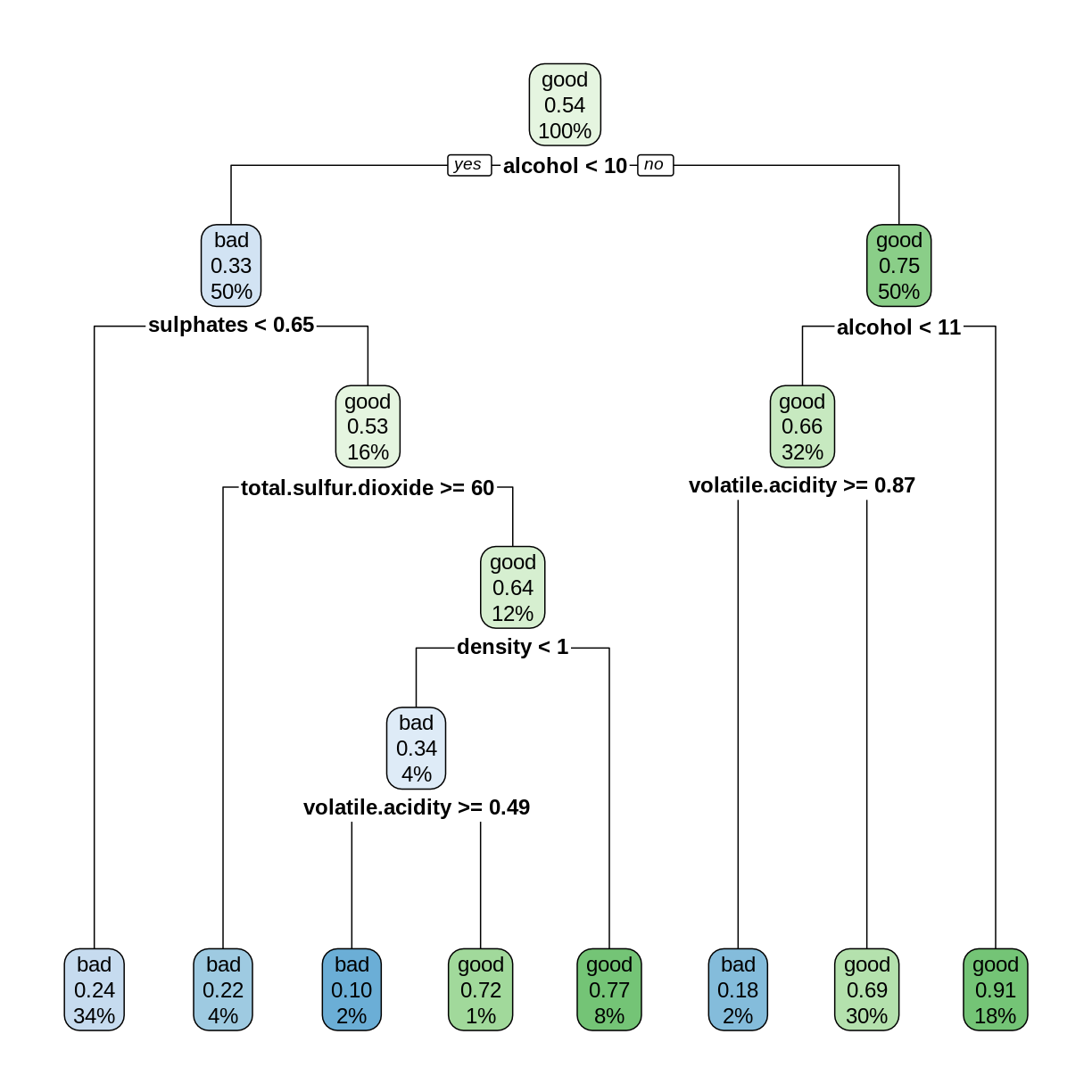
Challenge: Create a decision tree model
Use the
rpartfunction to create a decision tree model for predicting thegradevariable from the remaining columns in theredwineClassdata frame. Use the training and testing sets defined above. Compute the testing set accuracy.Solution
library(rpart) library(rpart.plot) rwtree <- rpart(grade ~ ., data = trainDF) rpart.plot(rwtree)
rwp <- predict(rwtree, testDF) rwpred <- ifelse(rwp[,1] > 0.5, "bad", "good") sum(testDF$grade == rwpred)/nrow(testDF)[1] 0.696875The decision tree model can correctly predict the grade about 70% of the time.
Random Forest Classification Model
A random forest model combines several decision tree models as follows.
- Several different decision trees are built, each from a random bootstrap sample of the same size as the original data. This process is also known as bagging (bootstrap aggregation).
- For each tree model, a randomly-chosen subset of variables is chosen to determine each split.
- Each decision tree model makes a prediction, and the category with the most “votes” is selected as the prediction of the random forest.
More details can be found in Breiman’s 2002 paper, pages 8-9.
The randomForest package is an R implementation of Breiman and Cutler’s original Fortran code. The syntax for building a model is similar to lm, glm, and rpart. Because of the randomness used in the algorithm, it is good practice to set the random seed so that the results will be reproducible.
library(randomForest)
set.seed(4567)
redwineForest <- randomForest(grade ~ ., data = trainDF)
The predict function works on random forests. Observe that it returns a vector of levels of the grade variable.
rwpred2 <- predict(redwineForest, testDF)
head(rwpred2)
1 2 3 4 5 6
bad bad bad bad bad bad
Levels: bad good
Challenge: Accuracy of the Random Forest Model
Compute the testing set accuracy of the random forest model above. Compare this accuracy with the decision tree model in the previous challenge.
Solution
sum(testDF$grade == rwpred2)/nrow(testDF)[1] 0.821875The random forest model can correctly predict the grade about 82% of the time, which is an improvement of about 12 percentage points over the decision tree model.
Out-of-bag Error
Since each tree in the random forest is built on a bootstrap sample of the rows in the training set, some rows will be left out of each sample. Each tree can then make a prediction on each row that was excluded, i.e., “out of the bag” (OOB). Each row will be excluded by several trees, which form a subforest that produces an aggregate prediction for each row. The out-of-bag estimate of the error rate is the error rate of these predictions. The OOB error rate gives a convenient estimate of the error rate of the model (error = 1 - accuracy). The print function reports the OOB error.
print(redwineForest)
Call:
randomForest(formula = grade ~ ., data = trainDF)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 19.16%
Confusion matrix:
bad good class.error
bad 470 119 0.2020374
good 126 564 0.1826087
The confusion matrix gives further details on how the OOB error was calculated: Out of 470+119 bad wines, 119 were classified as good, and out of 126+564 good wines, 126 were classified as bad. Check that (119+126)/(470+119+126+564) = 0.1916.
Train on the whole data set
Given that OOB error gives us a good way to estimate model accuracy, we can train random forest models on the entire data set, without using a train/test split (Breiman, 2001, p. 8).
set.seed(4567)
rwforFull <- randomForest(grade ~ ., data = redwineClass)
print(rwforFull)
Call:
randomForest(formula = grade ~ ., data = redwineClass)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 16.82%
Confusion matrix:
bad good class.error
bad 615 129 0.1733871
good 140 715 0.1637427
Caveat: If you plan to “tune” your model by adjusting the optional parameters in randomForest, it is still good practice to set aside a testing set for assessing model accuracy after the model has been tuned using only the training data. A train/test split is also helpful if you want to compare random forest models with other types of models.
Variable Importance
The out-of-bag errors can also be used to assess the importance of each explanatory variable in contributing to the accuracy of the model. If we set importance = TRUE in a call to randomForest, the function will keep track of how much the OOB accuracy decreases when each variable is randomly permuted. Scrambling a variable in this way effectively removes its predictive power from the model, so we would expect the most important variables to have the greatest decreases in accuracy.
set.seed(2345)
rwforFull <- randomForest(grade ~ ., data = redwineClass, importance = TRUE)
importance(rwforFull, type = 1)
MeanDecreaseAccuracy
fixed.acidity 33.60865
volatile.acidity 50.37700
citric.acid 30.12944
residual.sugar 31.40780
chlorides 34.39463
free.sulfur.dioxide 32.60753
total.sulfur.dioxide 50.95265
density 42.35901
pH 36.46366
sulphates 58.41187
alcohol 75.06260
Challenge: Most and Least Important
Based on the Mean Decrease in Accuracy, Which two variables are the most important, and which two are the least important? Are these results consistent with the decision tree model you constructed in the first challence of this episode?
Solution
For convenience, let’s sort the rows of the importance matrix.
importance(rwforFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(MeanDecreaseAccuracy))# A tibble: 11 × 2 Variable MeanDecreaseAccuracy <chr> <dbl> 1 alcohol 75.1 2 sulphates 58.4 3 total.sulfur.dioxide 51.0 4 volatile.acidity 50.4 5 density 42.4 6 pH 36.5 7 chlorides 34.4 8 fixed.acidity 33.6 9 free.sulfur.dioxide 32.6 10 residual.sugar 31.4 11 citric.acid 30.1The top two variables are
alcoholandsulphates, which both occur near the root of the decision tree. The least important variables areresidual.sugarandcitric.acid, which do not occur in the decision tree. So it seems consistent that the important variables play important roles in the decision tree, while the unimportant variables do not.
Red Wine Regression Model
So far, we have applied decision trees and random forests to classification problems, where the dependent variable is categorical. These techniques also apply to regression problems, where we are predicting a quantitative variable.
Recall that in the original wine data set, there is a variable called quality that assigns each sample a numerical quality score. For the examples that follow, we will treat quality as a quantitative variable. As before, we select the rows that contain observations of red wines, and we form training and testing sets.
redwine <- wine %>% slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% slice(trainIndex)
testDF <- redwine %>% slice(-trainIndex)
Fit a Decision Tree
When the dependent variable is quantitative, we use the method = "anova" option in rpart to construct a decision tree. In this situation, the predicted value corresponding to each node is the mean value of the observations assigned to the node, and the algorithm searches for a split that minimizes the sum of the squared errors of these predictions.
rwtree <- rpart(quality ~ ., data = trainDF, method = "anova")
rpart.plot(rwtree)
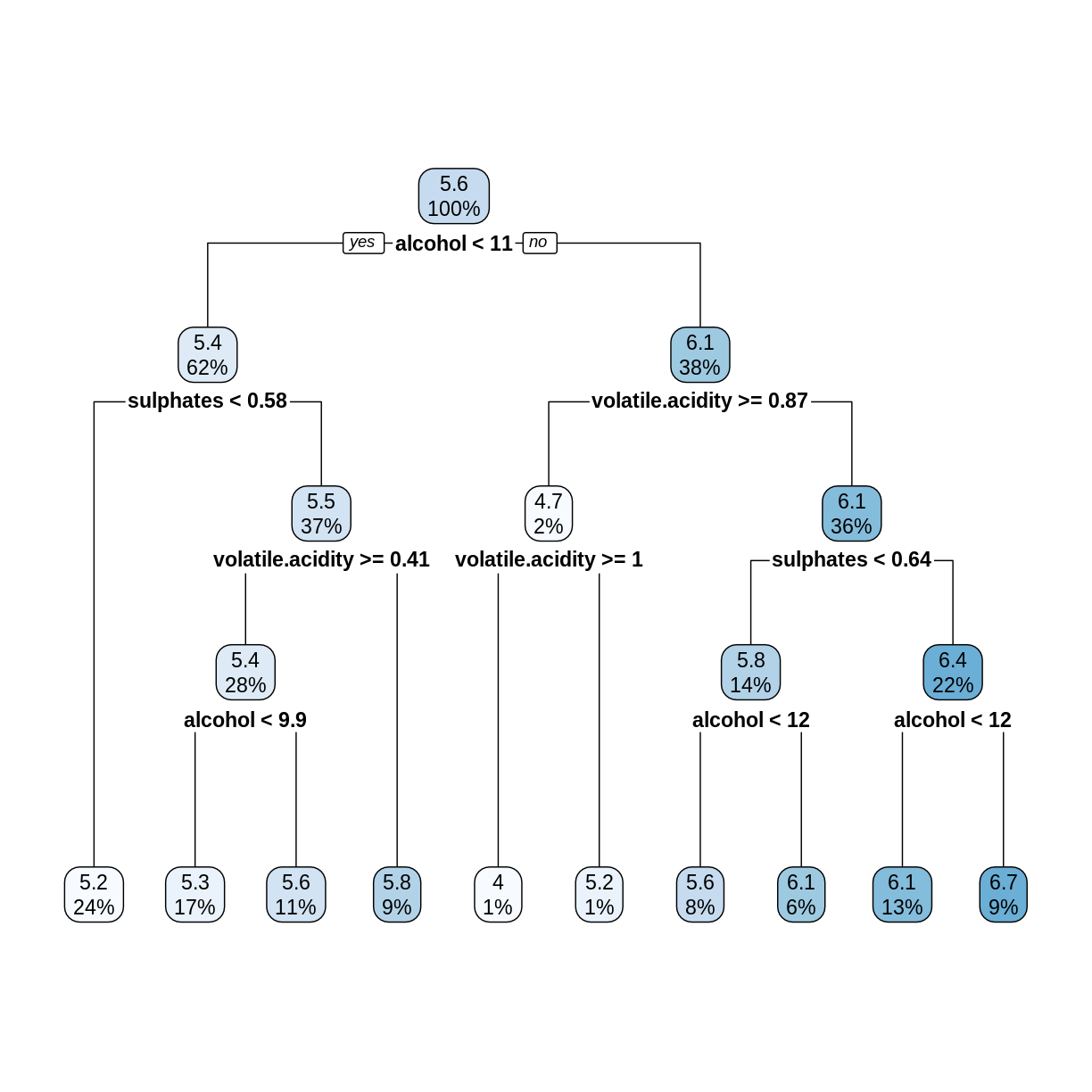
The rpart.plot command rounds off numerical values to save space. To see more digits of accuracy, print the tree in text format.
rwtree
n= 1279
node), split, n, deviance, yval
* denotes terminal node
1) root 1279 827.94210 5.636435
2) alcohol< 10.525 787 332.33800 5.364676
4) sulphates< 0.575 310 100.56770 5.154839 *
5) sulphates>=0.575 477 209.24950 5.501048
10) volatile.acidity>=0.405 364 149.63460 5.403846
20) alcohol< 9.85 223 66.76233 5.278027 *
21) alcohol>=9.85 141 73.75887 5.602837 *
11) volatile.acidity< 0.405 113 45.09735 5.814159 *
3) alcohol>=10.525 492 344.51020 6.071138
6) volatile.acidity>=0.8725 26 23.11538 4.730769
12) volatile.acidity>=1.015 10 6.00000 4.000000 *
13) volatile.acidity< 1.015 16 8.43750 5.187500 *
7) volatile.acidity< 0.8725 466 272.07730 6.145923
14) sulphates< 0.635 184 95.77717 5.831522
28) alcohol< 11.65 102 53.84314 5.627451 *
29) alcohol>=11.65 82 32.40244 6.085366 *
15) sulphates>=0.635 282 146.24470 6.351064
30) alcohol< 11.55 166 79.81325 6.138554 *
31) alcohol>=11.55 116 48.20690 6.655172 *
For example, the first split tests whether alcohol < 10.525, not 11 as shown in the plot of the tree.
Challenge: Check the Splits
In the above decision tree, consider the root (5.6), its left child (5.4), and the leftmost leaf (5.2). Check that these numbers are in fact the average
qualityvalues (rounded to one decimal place) of the observations intrainDFthat are assigned to each node.Solution
The root node contains all the observations, so compute its mean
qualityvalue.mean(trainDF$quality)[1] 5.636435The left child of the root contains observations where
alcoholis less than 10.525.trainDF %>% filter(alcohol < 10.525) %>% summarize(nodeValue = mean(quality))# A tibble: 1 × 1 nodeValue <dbl> 1 5.36The leftmost leaf contains observations where
alcoholis less than 10.525 andsulphatesis less than 0.575.trainDF %>% filter(alcohol < 10.525, sulphates < 0.575) %>% summarize(nodeValue = mean(quality))# A tibble: 1 × 1 nodeValue <dbl> 1 5.15
Decision Tree RMSE
For regression trees, each leaf is assigned a predicted value, and the predict function selects the appropriate leaf/prediction based on the values of the explanatory variables.
predictedQuality <- predict(rwtree, testDF)
head(predictedQuality)
1 2 3 4 5 6
5.154839 5.278027 5.278027 5.154839 5.154839 5.602837
Since this is a regression model, we assess its performance using the root mean squared error (RMSE).
errors <- predictedQuality - testDF$quality
decTreeRMSE <- sqrt(mean(errors^2))
decTreeRMSE
[1] 0.6862169
Random Forest Regression Model
Constructing a random forest regression model uses randomForest with the same syntax as we used for classification models. The only difference is that the response variable quality in our formula is a quantitative variable. The predicted values given by predict are the average predictions of all the trees in the forest.
set.seed(4567)
rwfor <- randomForest(quality ~ ., data = trainDF)
predQualRF <- predict(rwfor, testDF)
rfErrors <- predQualRF - testDF$quality
rfRMSE <- sqrt(mean(rfErrors^2))
rfRMSE
[1] 0.5913485
The random forest RMSE is better (smaller) than the decision tree RMSE.
print(rwfor)
Call:
randomForest(formula = quality ~ ., data = trainDF)
Type of random forest: regression
Number of trees: 500
No. of variables tried at each split: 3
Mean of squared residuals: 0.3269279
% Var explained: 49.5
The Mean of squared residuals is the MSE of the out-of-bag errors. The % Var explained term is a “pseudo R-squared”, computed as 1 - MSE/Var(y). The OOB MSE should be close to the MSE on the testing set. So again, you don’t always need a train/test split when working with random forests.
We conclude this episode with a series of challenges.
Challenge: Variable Importance
As with classification models, setting
importance = TRUEin a call torandomForestwill use the OOB errors to measure variable importance. In the regression case, the decrease in performance when a variable is permuted is measured by the percentage increase in MSE (%IncMSE). The larger the%IncMSE, the more important the variable.Compute the
%IncMSEvariable importance for the red wine regression model, and sort the variables by their importance. Re-train the model on the entireredwinedata set instead of on the testing set. Are the most important variables the same as in the classification model?Solution
The syntax is almost identical to the classification case. Since the identifier
%IncMSEcontains special characters, it must be enclosed in backticks.set.seed(2345) rwFull <- randomForest(quality ~ ., data = redwine, importance = TRUE) importance(rwFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(`%IncMSE`))# A tibble: 11 × 2 Variable `%IncMSE` <chr> <dbl> 1 alcohol 59.2 2 sulphates 55.6 3 volatile.acidity 39.7 4 total.sulfur.dioxide 38.3 5 density 34.5 6 chlorides 32.7 7 free.sulfur.dioxide 30.0 8 citric.acid 28.9 9 fixed.acidity 28.4 10 pH 25.1 11 residual.sugar 24.2The top five most important variables are the same as in the classification model, but their order is slightly different. The variable
pHseems to be relatively more important in the classification model.
Challenge: Linear Regression Model
In Episode 2, we used the
lmfunction to fit a linear model to the training set, and then we computed the RMSE on the testing set. Repeat this process for theredwinedata set. How does the linear regression RMSE compare to the random forest RMSE? Compare thesummaryof your linear model with the variable importance rankings from the previous challenge.Solution
redwine.lm <- lm(quality ~ ., data = trainDF) lmRMSE <- sqrt(mean((predict(redwine.lm, testDF) - testDF$quality)^2)) lmRMSE[1] 0.6880957The random forest RMSE is less than the linear model RMSE.
summary(redwine.lm)Call: lm(formula = quality ~ ., data = trainDF) Residuals: Min 1Q Median 3Q Max -2.68737 -0.36035 -0.03507 0.43456 1.95898 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.3242378 23.4596015 0.397 0.6911 fixed.acidity 0.0108114 0.0284758 0.380 0.7043 volatile.acidity -1.2144573 0.1320387 -9.198 < 2e-16 *** citric.acid -0.2957551 0.1608745 -1.838 0.0662 . residual.sugar 0.0193480 0.0168430 1.149 0.2509 chlorides -1.8858347 0.4583915 -4.114 4.14e-05 *** free.sulfur.dioxide 0.0054883 0.0023783 2.308 0.0212 * total.sulfur.dioxide -0.0034664 0.0007974 -4.347 1.49e-05 *** density -5.0636470 23.9244350 -0.212 0.8324 pH -0.4331191 0.2065623 -2.097 0.0362 * sulphates 0.9244109 0.1306583 7.075 2.47e-12 *** alcohol 0.2886439 0.0293633 9.830 < 2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.6385 on 1267 degrees of freedom Multiple R-squared: 0.3762, Adjusted R-squared: 0.3708 F-statistic: 69.46 on 11 and 1267 DF, p-value: < 2.2e-16The variables the smallest p-values (
Pr(>|t|)) tend to correspond to the most important variables in the random forest model.
Challenge: White Wine
Rows 1600-6497 of the
winedata frame correspond to white wine observations. Use these rows to train and test a random forest model, as we did with the red wine observations. Compute a testing set RMSE, and assess variable importance. Are the important variables for predicting white wine quality the same as the important variables for predicting red wine quality?Solution
whitewine <- wine %>% slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) wwfor <- randomForest(quality ~ ., data = trainDF) predQualww <- predict(wwfor, testDF) errors <- predQualww - testDF$quality wwRMSE <- sqrt(mean(errors^2))The RMSE on the white wine testing set is about 0.63.
set.seed(4567) wwforFull <- randomForest(quality ~ ., data = whitewine, importance = TRUE) importance(wwforFull, type = 1) %>% as_tibble(rownames = "Variable") %>% arrange(desc(`%IncMSE`))Relative to red wine,
free.sulfur.dioxideis much more important for predicting white wine quality, andsulphatesis less important.
Key Points
Random forests can make predictions of a categorical or quantitative variable.
Random forests, with their default settings, work reasonably well.