Linear and Logistic Regression
Overview
Teaching: 35 min
Exercises: 15 minQuestions
How can a model make predictions?
How do we measure the performance of predictions?
Objectives
Define a linear regression model.
Define a logistic regression model.
Split data into training and testing sets.
Kyphosis Data
Make sure the rpart package is loaded, and examine the structure of the kyphosis data frame.
library(rpart)
str(kyphosis)
'data.frame': 81 obs. of 4 variables:
$ Kyphosis: Factor w/ 2 levels "absent","present": 1 1 2 1 1 1 1 1 1 2 ...
$ Age : int 71 158 128 2 1 1 61 37 113 59 ...
$ Number : int 3 3 4 5 4 2 2 3 2 6 ...
$ Start : int 5 14 5 1 15 16 17 16 16 12 ...
Notice that there are 81 observations of four variables, so this is a rather small data set for machine learning techniques. In this episode, we will use this data set to illustrate the process of training and testing, where our models will be built using classical linear and logistic regression.
Make a training set and a test set
The first step in the process is to create a random train/test split of our data set. We will use the training set to build our model, without looking at the testing set. After our model is built, we will measure the accuracy of its predictions using the testing set.
There are various R packages that automate common tasks in machine learning, but it is instructive to use base R for now. The following commands will randomly select the row indexes of the training set (and therefore also of the testing set).
trainSize <- round(0.75 * nrow(kyphosis))
set.seed(6789) # so we all get the same random sets
trainIndex <- sample(nrow(kyphosis), trainSize)
Take a look at the trainIndex variable in the Environment tab of RStudio. Since we set a particular value for the random seed, we should all see the same sample of random numbers.
Next we form two data frames using these indexes. Recall that the selection of -trainIndex will select all rows whose indexes are not in the trainIndex vector.
trainDF <- kyphosis[trainIndex, ]
testDF <- kyphosis[-trainIndex, ]
We can View the train and test sets in RStudio to check that they form a random partition of the kyphosis data.
View(trainDF)
View(testDF)
Linear Regression as Supervised Learning
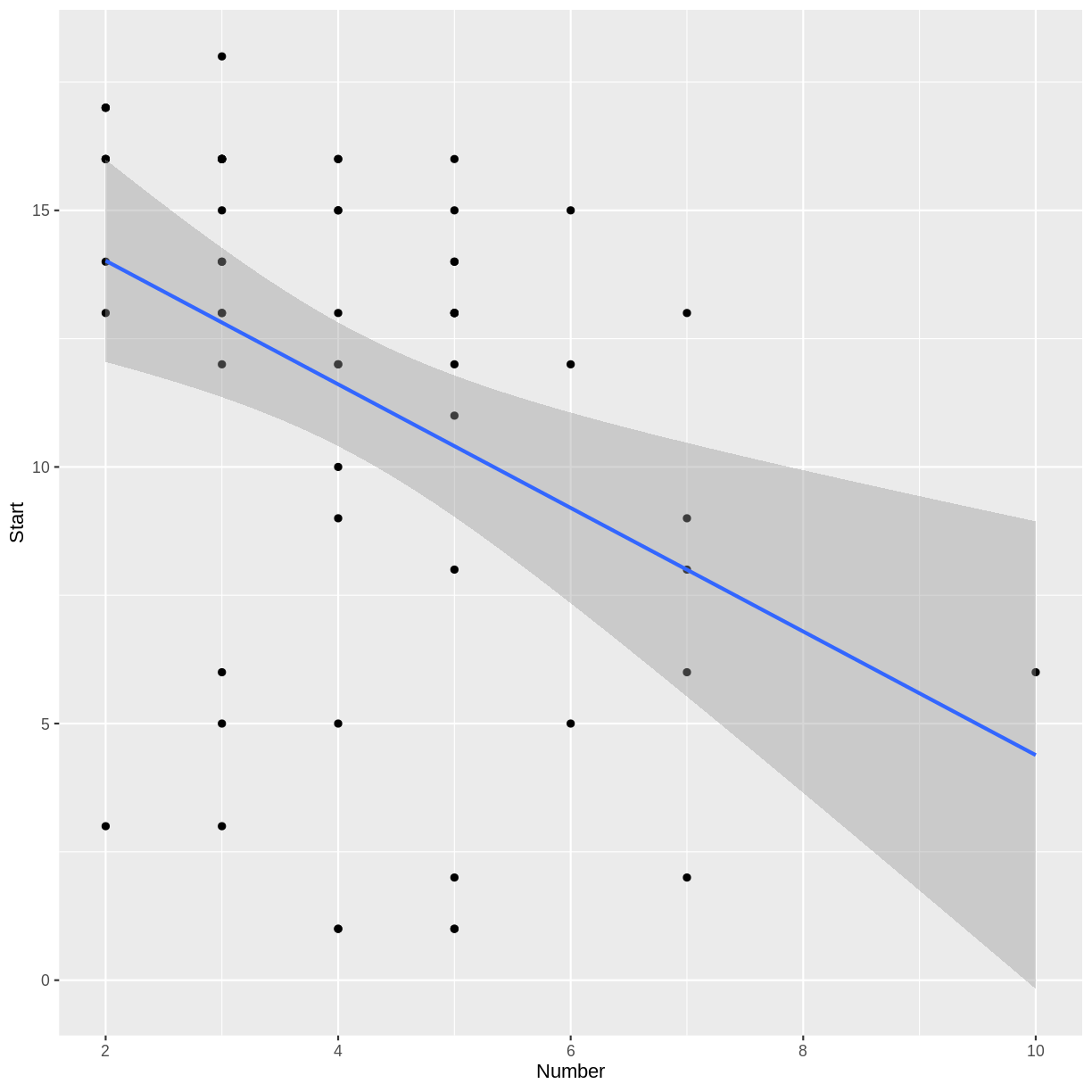
In the previous episode, we constructed a scatterplot of Number versus Start and observed a slight negative association. A model of this relationship is given by the least squares regression line, which we can consider as a simple example of supervised learning. To compute the slope and y-intercept of this line, we use the lm function in R.
In the following code block, the formula Start ~ Number specifies that Number is the explanatory (independent) variable, and Start is the response (dependent) variable. A helpful mnemonic is to read the ~ symbol as “as explained by.” To illustrate the process of supervised learning, we fit this regression line to the training set trainDF, saving the testing set for later.
model1 <- lm(Start ~ Number, data = trainDF)
summary(model1)
Call:
lm(formula = Start ~ Number, data = trainDF)
Residuals:
Min 1Q Median 3Q Max
-11.018 -1.610 1.615 3.186 5.798
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.4268 1.6393 10.021 2.38e-14 ***
Number -1.2041 0.3721 -3.236 0.00199 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.698 on 59 degrees of freedom
Multiple R-squared: 0.1507, Adjusted R-squared: 0.1364
F-statistic: 10.47 on 1 and 59 DF, p-value: 0.001988
The predicted Start is obtained by multiplying Number by the regression slope -1.2041 and adding the intercept 16.4268.
Challenge: Make a prediction and plot the regression line
- Predict the starting vertebra when the number of vertebrae involved is 3.
- Adding the term
geom_smooth(method = "lm")to a scatterplot will produce a plot of the regression line. Modify theggplotcode from the previous episode to create a scatterplot of the training data, along with a regression line.Solution
Three times -1.2041 plus 16.4268 is approximately 12.81.
library(ggplot2) # don't need this line if tidyverse is already loaded ggplot(trainDF, aes(x = Number, y = Start)) + geom_point() + geom_smooth(method = "lm")
Try the Testing Data Set
In R there is a generic method called predict that will make predictions given models of various types. For example, we can compute the predicted starting vertebrae for all the cases in our testing set as follows.
predictedStart <- predict(model1, testDF)
Challenge: Check our prediction
Check that the result of the
predictfunction agrees with the result of the previous challenge.Solution
head(predictedStart)12 21 32 36 37 38 12.81438 14.01851 14.01851 12.81438 12.81438 10.40611head(testDF)Kyphosis Age Number Start 12 absent 148 3 16 21 absent 22 2 16 32 absent 125 2 11 36 absent 93 3 16 37 absent 1 3 9 38 present 52 5 6Notice that the first row of our testing set has a
Numbervalue of 3, and the first value ofpredictedStartagrees with our answer to the previous challenge.
In general, the value of Start predicted by the model will not equal the actual value of Start in the testing set. However, in a good model, we would hope that the predicted values will be close to the actual values. To assess how close our predictions are to reality, we compute a vector of errors: predicted values minus actual values.
actualStart <- testDF$Start
errors <- predictedStart - actualStart
cat(round(errors, 1))
-3.2 -2 3 -3.2 3.8 4.4 0.2 2.6 10.6 2.8 -3.4 0.4 -3 -0.2 -0.2 1.6 -1.4 0.6 -5.6 -3.4
Measuring the Prediction Error
There are several ways to summarize the overall error in a regression model. The mean of the errors is not a good choice, because errors will usually have positive and negative values, which will cancel when averaged. To avoid this cancellation effect, we can take the mean of the squares of the errors: the Mean Squared Error, or MSE.
mean(errors^2)
[1] 13.14172
For a measurement of overall error in the same units as the output variable, we take the square root of the MSE to obtain the Root Mean Squared Error, or RMSE.
sqrt(mean(errors^2))
[1] 3.625151
Challenge: Mean Absolute Error
The Mean Absolute Error (MAE) is the average of the absolute values of the errors. Compute the MAE for the above example.
Solution
mean(abs(errors))[1] 2.77752
In upcoming episodes, we will compare different regression models using the RMSE of the prediction error on the testing set.
Logistic Regression
In the previous episode, we observed that in the context of the kyphosis data, it would be natural to try to predict whether a post-op kyphosis will be present, given the age of the patient, the number of vertebrae involved, and the number of the first vertebra operated on. In this situation, Kyphosis is our categorical response variable, and Age, Number, and Start are the explanatory variables. You can see the levels of the Kyphosis variable with the following command.
levels(kyphosis$Kyphosis)
[1] "absent" "present"
Since our response variable is categorical, we need to employ a classification model. The following command will fit a Multiple Logistic Regression model to our training data using the glm command.
model2 <- glm(Kyphosis ~ Age + Number + Start, data = trainDF, family = "binomial")
Notice that we specified the formula Kyphosis ~ Age + Number + Start, because Kyphosis is the response variable and Age, Number, and Start are the explanatory variables. Since Age, Number, and Start make up all the remaining columns in our data frame, we could have used the equivalent formula Kyphosis ~ ., as follows.
model2 <- glm(Kyphosis ~ ., data = trainDF, family = "binomial")
The formula Kyphosis ~ . can be read as “Kyphosis as explained by everything else.”
The predict function for binomial glm models will return predicted probabilities of the response variable if we specify the option type = "response".
predict(model2, testDF, type = "response")
12 21 32 36 37 38
0.060991556 0.004837329 0.066676823 0.027771160 0.034862103 0.389677526
39 43 44 46 47 51
0.287882930 0.988363673 0.531083119 0.183999574 0.122064478 0.244337950
52 57 60 66 68 69
0.003170923 0.014410381 0.061131542 0.069057143 0.236889844 0.056456800
70 76
0.035581184 0.206575349
If we actually want to know whether or not the model predicts that a kyphosis is present, we need to convert these probabilities to the appropriate levels of the Kyphosis variable.
The first level, absent, corresponds to probabilities near zero, and the second level, present, corresponds to probabilities near one. So we can create a vector of the predicted Kyphosis values of our testing set as follows.
predictedKyphosis <- ifelse(predict(model2, testDF, type = "response") < 0.5,
"absent", "present")
predictedKyphosis
12 21 32 36 37 38 39 43
"absent" "absent" "absent" "absent" "absent" "absent" "absent" "present"
44 46 47 51 52 57 60 66
"present" "absent" "absent" "absent" "absent" "absent" "absent" "absent"
68 69 70 76
"absent" "absent" "absent" "absent"
The actual occurrences of kyphosis in our testing set are given by the vector testDF$Kyphosis, so the following command will tell us which predictions were correct.
testDF$Kyphosis == predictedKyphosis
12 21 32 36 37 38 39 43 44 46 47 51 52
TRUE TRUE TRUE TRUE TRUE FALSE TRUE FALSE FALSE FALSE TRUE TRUE TRUE
57 60 66 68 69 70 76
TRUE TRUE TRUE TRUE TRUE TRUE TRUE
One way to measure the performance of a classification model is to report the proportion of correct predictions, known as the accuracy of the model. Recall that the sum function, when applied to a logical vector, will return the number of TRUEs in the vector.
accuracy <- sum(testDF$Kyphosis == predictedKyphosis)/nrow(testDF)
cat("Proportion of correct predictions using testing data: ", accuracy, "\n")
Proportion of correct predictions using testing data: 0.8
cat("Testing data error rate: ", 1-accuracy, "\n")
Testing data error rate: 0.2
Challenge: Try different train/test splits
Before we constructed the models in this episode, we divided the data into a training set and a testing set. Try experimenting with different train/test splits to see if it has any effect on the model accuracy. Specifically, re-do the construction of
model2, the logistic regression model, with the following modifications.
Try a different value of the random seed. Does the prediction accuracy change?
We originally chose a training set size that was 75% of the size of the
kyphosisdata frame. Experiment with different percentages for the train/test split. Does changing the size of the training set affect the accuracy of the model?Solution
Let’s define a function to avoid repeating code.
testAccuracy <- function(splitPercent, randomSeed) { tSize <- round(splitPercent * nrow(kyphosis)) set.seed(randomSeed) tIndex <- sample(nrow(kyphosis), tSize) trnDF <- kyphosis[tIndex, ] tstDF <- kyphosis[-tIndex, ] kmod <- glm(Kyphosis ~ ., data = trnDF, family = "binomial") predK <- ifelse(predict(kmod, tstDF, type = "response") < 0.5, "absent", "present") return(sum(tstDF$Kyphosis == predK)/nrow(tstDF)) }Try different seeds:
testAccuracy(0.75, 6789) # our original settings[1] 0.8testAccuracy(0.75, 1234)[1] 0.9So the choice of seed makes a difference.
Try different split percentages:
testAccuracy(0.9, 6789)[1] 0.75testAccuracy(0.5, 6789)[1] 0.7804878
Key Points
Classical linear and logistic regression models can be thought of as examples of regression and classification models in machine learning.
Testing sets can be used to measure the performance of a model.