Gradient Boosted Trees
Overview
Teaching: 45 min
Exercises: 25 minQuestions
What is gradient boosting?
How can we train an XGBoost model?
What is the learning rate?
Objectives
Introduce XGBoost models.
Train regression models using XGBoost
Explore the effect of learning rate on the training process.
Gradient Boosted Trees
A random forest is called an ensemble method, because it combines the results of a set of trees to form a single prediction. Gradient boosted trees are also ensemble methods, but instead of forming a forest of trees from different random samples, they grow successive trees that systematically reduce the error of the model at each iteration.
We will be using the R package xgboost, which gives a fast, scalable implementation of a gradient boosting framework. For more information on how xgboost works, see the XGBoost Presentation vignette and the Introduction to Boosted Trees tutorial in the XGBoost documentation. In this episode we will use XGBoost to create a regression model, but this framework can also be used for classification problems.
Reload the Red Wine Data
library(tidyverse)
library(here)
library(xgboost)
Attaching package: 'xgboost'
The following object is masked from 'package:dplyr':
slice
Notice that both xgboost and dplyr have a function called slice. In the following code block, we specify that we want to use the dplyr version.
wine <- read_csv(here("data", "wine.csv"))
redwine <- wine %>% dplyr::slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% dplyr::slice(trainIndex)
testDF <- redwine %>% dplyr::slice(-trainIndex)
The xgboost package defines a data structure called xgb.DMatrix that optimizes storage and retrieval. To use the advanced features of xgboost, it is necessary to convert our training and test sets to the xgb.DMatrix class.
dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality)
dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)
Training an XGBoost Model
Since we specified a label in our dtrain and dtest matrices, there is no need to specify a formula when training a model using xgb.train. The label that we specified (quality rating) will be the response variable, and the columns of the data that we specified will be the explanatory variables. One option that we must specify is nrounds, which restricts the number of boosting iterations the algorithm will make.
redwineXGB <- xgb.train(data = dtrain, nrounds = 10)
Let’s calculate the RMSE on our testing set. The predict function for XGBoost models expects a matrix, so we pass it the xgb.DMatrix that we created from our testing set.
pQuality <- predict(redwineXGB, dtest)
errors <- pQuality - testDF$quality
sqrt(mean(errors^2)) #RMSE
[1] 0.6653935
More Details on the Training Process
The xgb.train command will automatically calculate the RMSE on our testing set after each iteration if we set the testing set in the watchlist.
redwineXGB <- xgb.train(data = dtrain, watchlist = list(test = dtest), nrounds = 10)
[1] test-rmse:3.676492
[2] test-rmse:2.620643
[3] test-rmse:1.904736
[4] test-rmse:1.414777
[5] test-rmse:1.110905
[6] test-rmse:0.913236
[7] test-rmse:0.793578
[8] test-rmse:0.729415
[9] test-rmse:0.686777
[10] test-rmse:0.665393
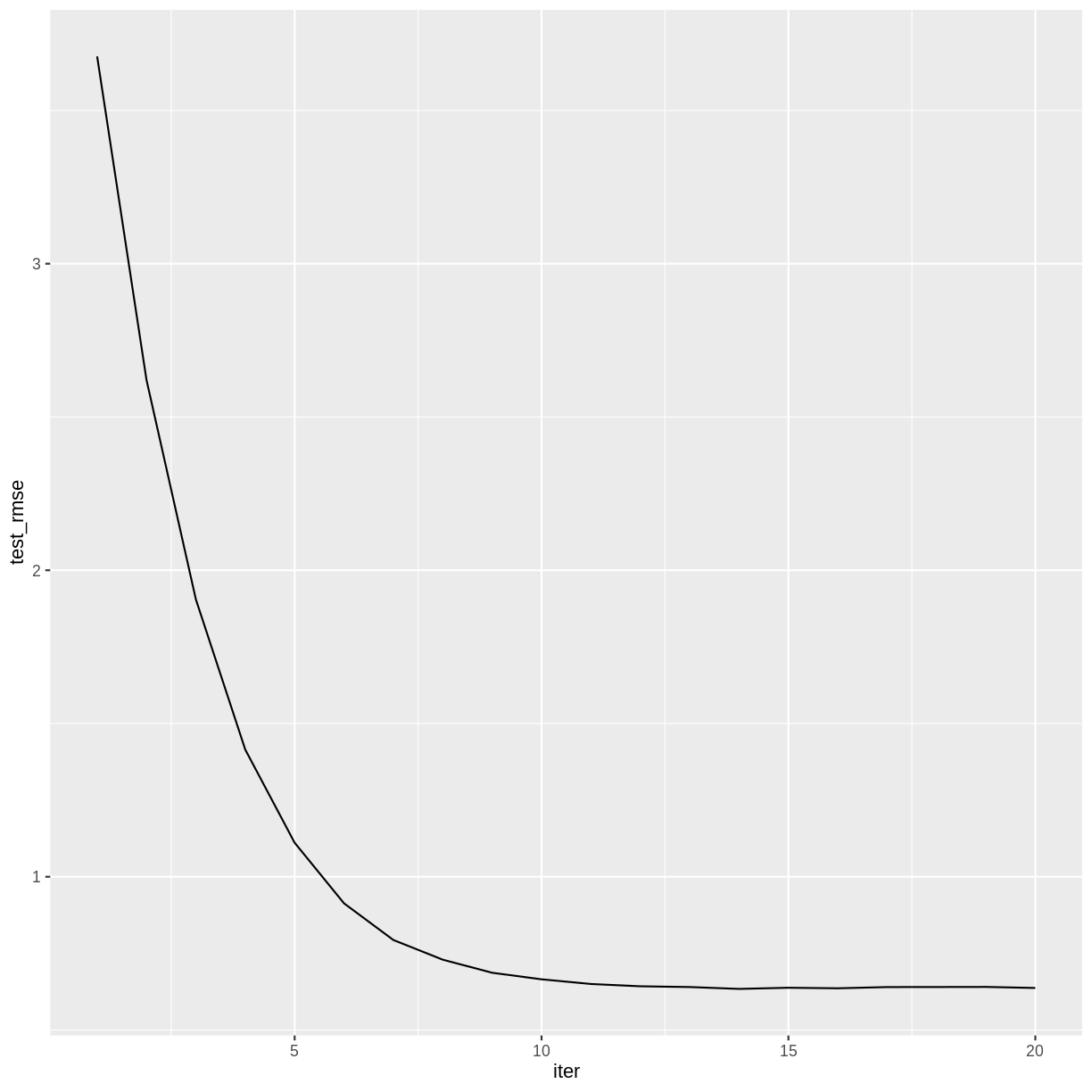
The training history is saved as a data frame in the variable gbm$evaluation_log, so we can plot how the RMSE changes during the training process.
redwineXGB$evaluation_log %>%
ggplot(aes(x = iter, y = test_rmse)) +
geom_line()
Challenge: How many boosting iterations?
Experiment with different values of
nroundsin the above call toxgb.train. Does the accuracy of the model improve with more iterations? Is there a point after which the model ceases to improve?Solution
The accuracy of the model doesn’t appear to improve after iteration 14.
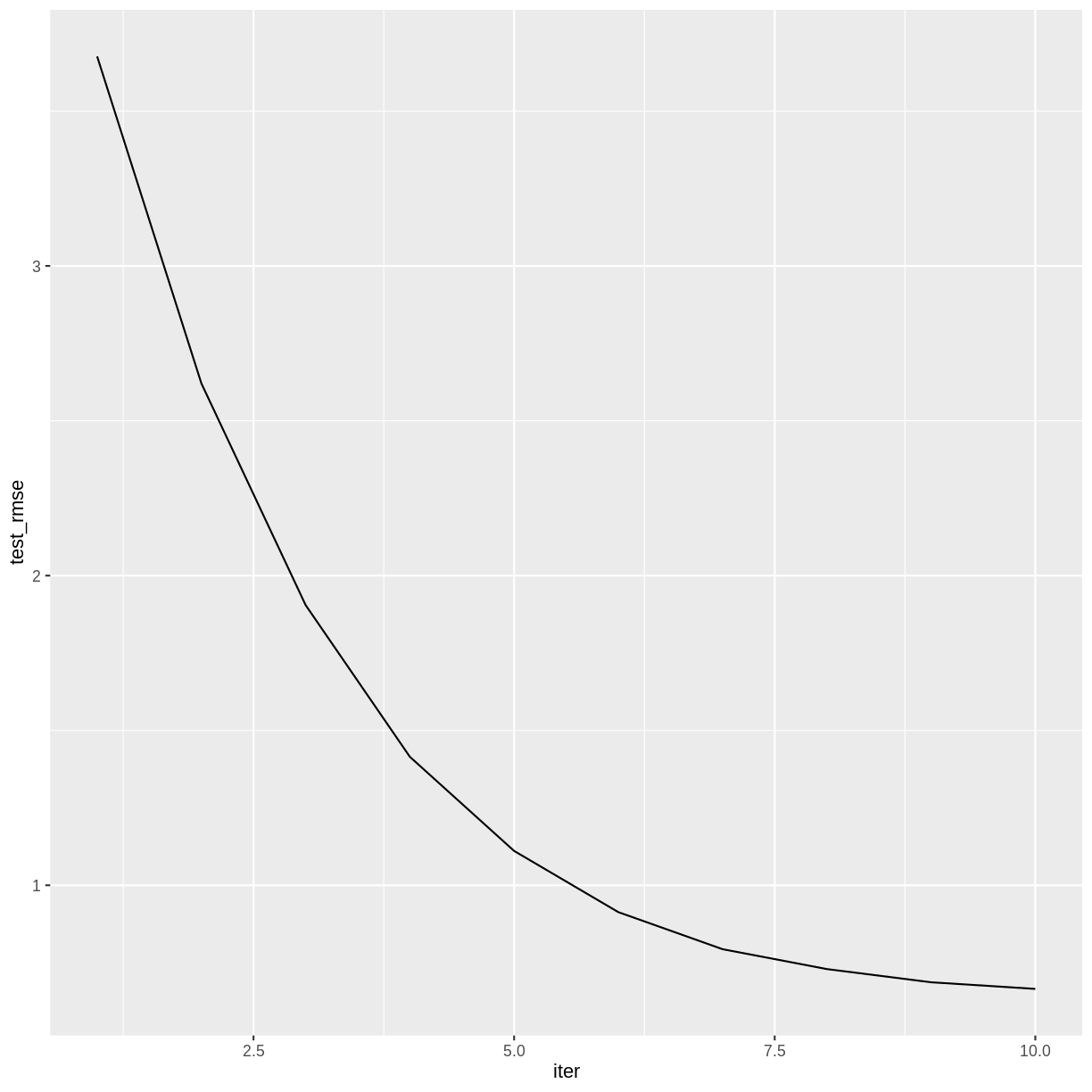
redwineXGB <- xgb.train(data = dtrain, watchlist = list(test = dtest), nrounds = 20)[1] test-rmse:3.676492 [2] test-rmse:2.620643 [3] test-rmse:1.904736 [4] test-rmse:1.414777 [5] test-rmse:1.110905 [6] test-rmse:0.913236 [7] test-rmse:0.793578 [8] test-rmse:0.729415 [9] test-rmse:0.686777 [10] test-rmse:0.665393 [11] test-rmse:0.650133 [12] test-rmse:0.642655 [13] test-rmse:0.640231 [14] test-rmse:0.634134 [15] test-rmse:0.637910 [16] test-rmse:0.636140 [17] test-rmse:0.640103 [18] test-rmse:0.640305 [19] test-rmse:0.640569 [20] test-rmse:0.637183redwineXGB$evaluation_log %>% ggplot(aes(x = iter, y = test_rmse)) + geom_line()
Learning Rate
Machine learning algorithms that reduce a loss function over a sequence of iterations typically have a setting that controls the learning rate. A smaller learning rate will generally reduce the error by a smaller amount at each iteration, and therefore will require more iterations to arrive at a given level of accuracy. The advantage to a smaller learning rate is that the algorithm is less likely to overshoot the optimum fit.
In XGBoost, the setting that controls the learning rate is called eta, which is one of several hyperparameters that can be adjusted. Its default value is 0.3, but smaller values will usually perform better. It must take a value in the range 0 < eta < 1.
The following code will set eta to its default value. We include a value for early_stopping_rounds, which will halt the training after a specified number of iterations pass without improvement. When using early_stopping_rounds, nrounds can be set to a very large number. To avoid printing too many lines of output, we also set a value for print_every_n.
redwineXGB <- xgb.train(data = dtrain,
params = list(eta = 0.3),
watchlist = list(test = dtest),
nrounds = 1000,
early_stopping_rounds = 10,
print_every_n = 5)
[1] test-rmse:3.676492
Will train until test_rmse hasn't improved in 10 rounds.
[6] test-rmse:0.913236
[11] test-rmse:0.650133
[16] test-rmse:0.636140
[21] test-rmse:0.639540
Stopping. Best iteration:
[14] test-rmse:0.634134
The 14th iteration had the smallest RMSE, as we found in the previous challenge.
Challenge: Experiment with the learning rate.
Experiment with different values of
etain the above call toxgb.train. Notice how smaller values of eta require more iterations. Can you find a value ofetathat results in a lower testing set RMSE than the default?Solution
A learning rate around 0.1 reduces the RMSE somewhat.
redwineXGB <- xgb.train(data = dtrain, params = list(eta = 0.1), watchlist = list(test = dtest), nrounds = 1000, early_stopping_rounds = 10, print_every_n = 15)[1] test-rmse:4.689984 Will train until test_rmse hasn't improved in 10 rounds. [16] test-rmse:1.164598 [31] test-rmse:0.655252 [46] test-rmse:0.618707 [61] test-rmse:0.617009 [76] test-rmse:0.612820 Stopping. Best iteration: [75] test-rmse:0.612406
Variable Importance
As with random forests, you can view the predictive importance of each explanatory variable.
xgb.importance(model = redwineXGB)
Feature Gain Cover Frequency
1: alcohol 0.33236129 0.11264259 0.07936508
2: volatile.acidity 0.12367170 0.09820458 0.11922399
3: sulphates 0.10975935 0.10726694 0.08218695
4: total.sulfur.dioxide 0.07500529 0.13655797 0.09276896
5: density 0.05960668 0.09451465 0.08500882
6: chlorides 0.05883225 0.10318293 0.09805996
7: residual.sugar 0.05499778 0.09106117 0.08818342
8: fixed.acidity 0.05087633 0.07920964 0.14250441
9: pH 0.04772447 0.06078573 0.06807760
10: citric.acid 0.04532904 0.07698668 0.07830688
11: free.sulfur.dioxide 0.04183582 0.03958713 0.06631393
The rows are sorted by Gain, which measures the accuracy improvement contributed by a feature based on all the splits it determines. Note that the sum of all the gains is 1.
Training Error vs. Testing Error
Like many machine learning algorithms, gradient boosting operates by minimizing the error on the training set. However, we evaluate its performance by computing the error on the testing set. These two errors are usually different, and it is not uncommon to have much lower training RMSE than testing RMSE.
To see both training and testing errors, we can add a train item to the watchlist.
redwineXGB <- xgb.train(data = dtrain,
params = list(eta = 0.1),
watchlist = list(train = dtrain, test = dtest),
nrounds = 1000,
early_stopping_rounds = 10,
print_every_n = 15)
[1] train-rmse:4.690120 test-rmse:4.689984
Multiple eval metrics are present. Will use test_rmse for early stopping.
Will train until test_rmse hasn't improved in 10 rounds.
[16] train-rmse:1.109302 test-rmse:1.164598
[31] train-rmse:0.467275 test-rmse:0.655252
[46] train-rmse:0.369513 test-rmse:0.618707
[61] train-rmse:0.328256 test-rmse:0.617009
[76] train-rmse:0.290210 test-rmse:0.612820
Stopping. Best iteration:
[75] train-rmse:0.291627 test-rmse:0.612406
redwineXGB$evaluation_log %>%
pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>%
ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()
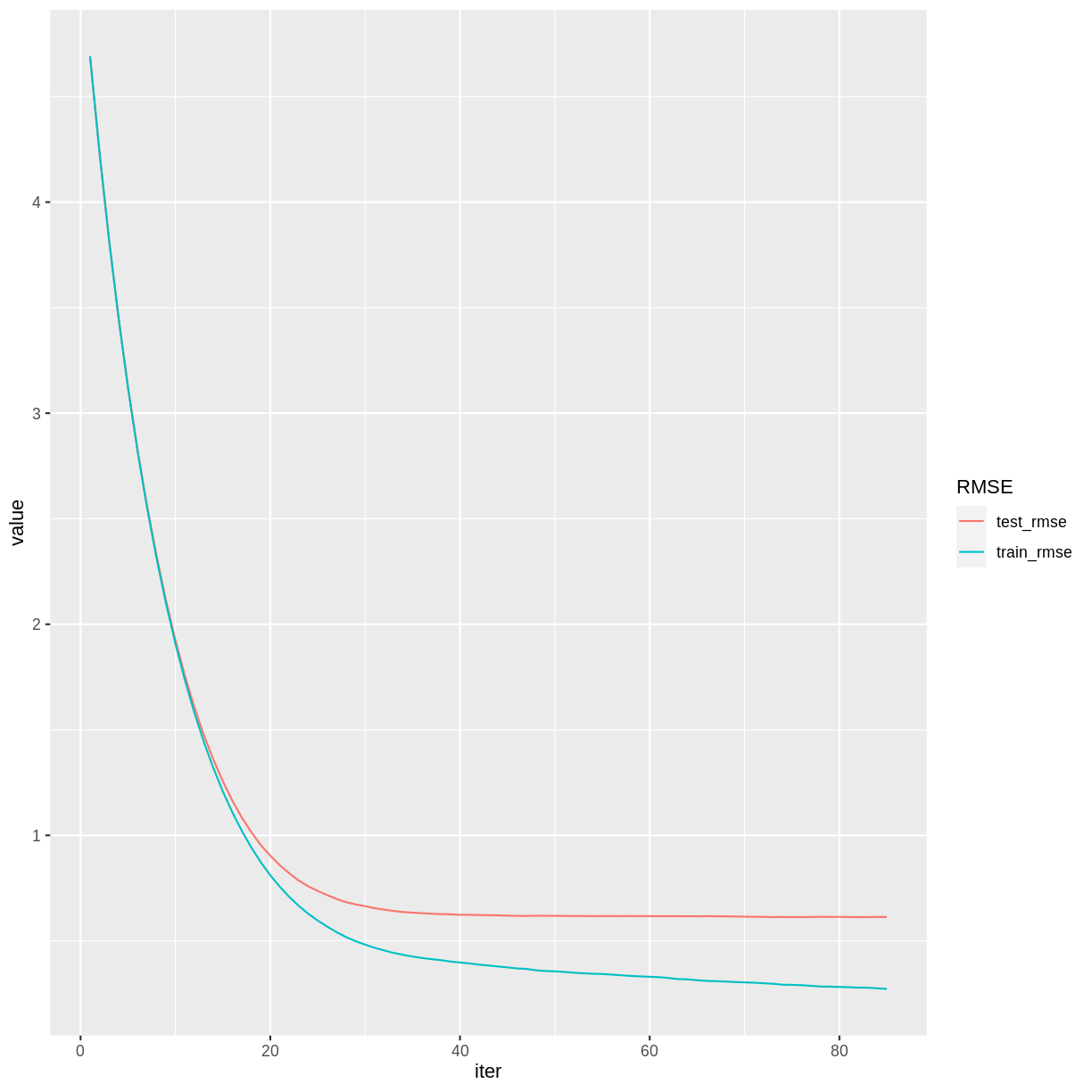
Notice that beyond iteration 40 or so, the training RMSE continues to decrease while the testing RMSE has basically stabilized. This divergence indicates that the later training iterations are improving the model based on the particularities of the training set, but in a way that does not generalize to the testing set.
Saving a trained model
As models become more complicated, the time it takes to train them becomes nontrivial. For this reason, it can be helpful to save a trained XGBoost model. We’ll create a directory in our project called saved_models and save our XGBoost model in a universal binary format that can be read by any XGBoost interface (e.g., R, Python, Julia, Scala).
dir.create(here("saved_models"))
xgb.save(redwineXGB, here("saved_models", "redwine.model"))
This trained model can be loaded into a future R session with the xgb.load command.
reloaded_model <- xgb.load(here("saved_models", "redwine.model"))
However, while reloaded_model can be used with the predict function, it is not identical to the redwineXGB object. For reproducibility, it is important to save the source code used in the training process.
Challenge: White Wine
Build an XGBoost model for the white wine data (rows 1600-6497) of the
winedata frame. Compare the RMSE and variable importance with the random forest white wine model from the previous episode.Solution
whitewine <- wine %>% dplyr::slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality) dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality) whitewineXGB <- xgb.train(data = dtrain, params = list(eta = 0.1), watchlist = list(train = dtrain, test = dtest), nrounds = 1000, early_stopping_rounds = 10, print_every_n = 20) xgb.importance(model = whitewineXGB) whitewineXGB$evaluation_log %>% pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>% ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()The testing set RMSE (0.664) is worse than what we obtained in the random forest model (0.63). The important explanatory variables are similar.
So far, our XGBoost models have performed slightly worse than the equivalent random forest models. In the next episode we will explore ways to improve these results.
Key Points
Gradient boosted trees can be used for the same types of problems that random forests can solve.
The learning rate can affect the performance of a machine learning algorithm.