Cross Validation and Tuning
Overview
Teaching: 45 min
Exercises: 30 minQuestions
How can the fit of an XGBoost model be improved?
What is cross validation?
What are some guidelines for tuning parameters in a machine learning algorithm?
Objectives
Explore the effects of adjusting the XGBoost parameters.
Practice some coding techniques to tune parameters using grid searching and cross validation.
Parameter Tuning
Like many other machine learning algorithms, XGBoost has an assortment of parameters that control the behavior of the training process. (These parameters are sometimes referred to as hyperparameters, because they cannot be directly estimated from the data.) To improve the fit of the model, we can adjust, or tune, these parameters. According to the notes on parameter tuning in the XGBoost documentation, “[p]arameter tuning is a dark art in machine learning,” so it is difficult to prescribe an automated process for doing so. In this episode we will develop some coding practices for tuning an XGBoost model, but be advised that the optimal way to tune a model will depend heavily on the given data set.
You can find a complete list of XGBoost parameters in the documentation. Generally speaking, each parameter controls the complexity of the model in some way. More complex models tend to fit the training data more closely, but such models can be very sensitive to small changes in the training set. On the other hand, while less complex models can be more conservative in this respect, they have a harder time modeling intricate relationships. The “art” of parameter tuning lies in finding an appropriately complex model for the problem at hand.
A complete discussion of the issues involved are beyond the scope of this lesson. An excellent resource on the topic is An Introduction to Statistical Learning, by James, Witten, Hastie, and Tibshirani. In particular, Section 2.2.2 discusses the Bias-Variance Trade-Off inherent in statistical learning methods.
Cross Validation
How will we be able to tell if an adjustment to a parameter has improved the model? One possible approach would be to test the model before and after the adjustment on the testing set. However, the problem with this method is that it runs the risk of tuning the model to the particular properties of the testing set, rather than to general future cases that we might encounter. It is better practice to save our testing set until the very end of the process, and then use it to test the accuracy of our model. Training set accuracy, as we have seen, tends to underestimate the accuracy of a machine learning model, so tuning to the training set may also fail to make improvements that generalize.
An alternative testing procedure is to use cross validation on the training set to judge the effect of tuning adjustments. In k-fold cross validation, the training set is partitioned randomly into k subsets. Each of these subsets takes a turn as a testing set, while the model is trained on the remaining data. The accuracy of the model is then measured k times, and the results are averaged to obtain an estimate of the overall model performance. In this way we can be more certain that repeated adjustments will be tested in ways that generalize to future observations. It also allows us to save the original testing set for a final test of our tuned model.
Revisit the Red Wine Quality Model
Let’s see if we can improve the previous episode’s model for predicting red wine quality.
library(tidyverse)
library(here)
library(xgboost)
wine <- read_csv(here("data", "wine.csv"))
redwine <- wine %>% dplyr::slice(1:1599)
trainSize <- round(0.80 * nrow(redwine))
set.seed(1234)
trainIndex <- sample(nrow(redwine), trainSize)
trainDF <- redwine %>% dplyr::slice(trainIndex)
testDF <- redwine %>% dplyr::slice(-trainIndex)
dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality)
dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)
The xgb.cv command handles most of the details of the cross validation process. Since this is a random process, we will set a seed value for reproducibility. We will use 10 folds and the default value of 0.3 for eta.
set.seed(524)
rwCV <- xgb.cv(params = list(eta = 0.3),
data = dtrain,
nfold = 10,
nrounds = 500,
early_stopping_rounds = 10,
print_every_n = 5)
[1] train-rmse:3.676824+0.003733 test-rmse:3.682796+0.044551
Multiple eval metrics are present. Will use test_rmse for early stopping.
Will train until test_rmse hasn't improved in 10 rounds.
[6] train-rmse:0.808822+0.003848 test-rmse:0.888110+0.043011
[11] train-rmse:0.418891+0.013364 test-rmse:0.641062+0.037335
[16] train-rmse:0.343756+0.012450 test-rmse:0.628046+0.033493
[21] train-rmse:0.299929+0.010728 test-rmse:0.625757+0.033106
[26] train-rmse:0.258271+0.013402 test-rmse:0.624861+0.036458
[31] train-rmse:0.225188+0.013268 test-rmse:0.623947+0.042251
[36] train-rmse:0.194026+0.011849 test-rmse:0.624094+0.042001
Stopping. Best iteration:
[29] train-rmse:0.236075+0.013368 test-rmse:0.622687+0.041345
The output appears similar to the xgb.train command. Notice that each error estimate now includes a standard deviation, because these estimates are formed by averaging over all ten folds. The function returns a list, which we have given the name rwCV. Its names hint at what each list item represents.
names(rwCV)
[1] "call" "params" "callbacks" "evaluation_log"
[5] "niter" "nfeatures" "folds" "best_iteration"
[9] "best_ntreelimit"
Challenge: Examine the cross validation results
- Examine the list item
rwCV$folds. What do suppose these numbers represent? Are all the folds the same size? Can you explain why/why not?- Display the evaluation log with rows sorted by
test_rmse_mean.- How could you display only the row containing the best iteration?
Solution
- The numbers are the indexes of the rows in each fold. The folds are not all the same size, because no row can be used more than once, and there are 1279 rows total in the training set, so they don’t divide evenly into 10 partitions.
rwCV$evaluation_log %>% arrange(test_rmse_mean)iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std 1: 29 0.2360750 0.013368348 0.6226874 0.04134490 2: 35 0.2007999 0.011608484 0.6229431 0.04233848 3: 33 0.2134821 0.012373642 0.6229542 0.04233916 4: 32 0.2192703 0.013306955 0.6229588 0.04129835 5: 34 0.2076733 0.012222030 0.6233336 0.04166854 6: 28 0.2426037 0.013287443 0.6233426 0.03899304 7: 31 0.2251878 0.013267807 0.6239475 0.04225134 8: 36 0.1940258 0.011849455 0.6240940 0.04200144 9: 30 0.2310984 0.012281978 0.6241792 0.04091916 10: 27 0.2507866 0.013086816 0.6241843 0.03830991 11: 37 0.1893309 0.011079029 0.6243738 0.04193406 12: 25 0.2659939 0.012269906 0.6245430 0.03553351 13: 39 0.1790856 0.011285008 0.6245503 0.04176559 14: 38 0.1846427 0.010905405 0.6247798 0.04141676 15: 26 0.2582708 0.013402250 0.6248607 0.03645813 16: 23 0.2835744 0.010293100 0.6256707 0.03261529 17: 21 0.2999289 0.010728491 0.6257569 0.03310647 18: 18 0.3203636 0.010830155 0.6257911 0.03230540 19: 22 0.2910245 0.011284146 0.6259865 0.03283513 20: 24 0.2760180 0.012458570 0.6260504 0.03340596 21: 20 0.3067600 0.010738381 0.6262777 0.03185302 22: 17 0.3320214 0.011822742 0.6271510 0.03445198 23: 19 0.3119272 0.010392821 0.6272786 0.03191304 24: 15 0.3564079 0.012468678 0.6273193 0.03434991 25: 16 0.3437564 0.012450158 0.6280460 0.03349317 26: 14 0.3679581 0.011806629 0.6285073 0.03311778 27: 13 0.3802030 0.011004878 0.6307059 0.03545827 28: 12 0.3983362 0.010466897 0.6353593 0.03506220 29: 11 0.4188905 0.013364106 0.6410624 0.03733492 30: 10 0.4497433 0.011540044 0.6501031 0.04014740 31: 9 0.4915645 0.010805274 0.6679334 0.03942590 32: 8 0.5556933 0.007217608 0.7061343 0.03954675 33: 7 0.6565486 0.004032585 0.7713876 0.04152207 34: 6 0.8088225 0.003847863 0.8881101 0.04301120 35: 5 1.0398669 0.003228572 1.0914671 0.04090907 36: 4 1.3825695 0.002820641 1.4113087 0.03738249 37: 3 1.8857284 0.002530300 1.9004059 0.04118868 38: 2 2.6184095 0.002917347 2.6270221 0.04337352 39: 1 3.6768236 0.003733214 3.6827955 0.04455107 iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_stdrwCV$evaluation_log[rwCV$best_iteration]iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std 1: 29 0.236075 0.01336835 0.6226874 0.0413449
Repeat Cross Validation in a Loop
To expedite the tuning process, it helps to design a loop to run repeated cross validations on different parameter values. We can start by choosing a value of eta from a list of candidate values.
paramDF <- tibble(eta = c(0.001, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4))
The following command converts a data frame to a list of lists. The split function splits paramDF into a list of its rows, and then the lapply function converts each row to a list. Each item of paramlist will be a list giving a valid parameter setting that we can use in the xgb.cv function.
paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list)
Now we will write a loop that will perform a different cross validation for each parameter setting in the paramList list. We’ll keep track of the best iterations in the bestResults tibble. To avoid too much printing, we set verbose = FALSE and use a txtProgressBar to keep track of our progress. On some systems, it may be necessary to use gc() to prevent running out of memory.
bestResults <- tibble()
set.seed(708)
pb <- txtProgressBar(style = 3)
for(i in seq(length(paramList))) {
rwCV <- xgb.cv(params = paramList[[i]],
data = dtrain,
nrounds = 500,
nfold = 10,
early_stopping_rounds = 10,
verbose = FALSE)
bestResults <- bestResults %>%
bind_rows(rwCV$evaluation_log[rwCV$best_iteration])
gc() # Free unused memory after each loop iteration
setTxtProgressBar(pb, i/length(paramList))
}
close(pb) # done with the progress bar
We now have all of the best iterations in the bestResults data frame, which we can combine with the data frame of parameter values.
etasearch <- bind_cols(paramDF, bestResults)
In RStudio, it is convenient to use View(etasearch) to view the results in a separate tab. We can use the RStudio interface to sort by mean_test_rmse.
Note that there is not much difference in mean_test_rmse among the best three choices. As we have seen in the previous episode, the choice of eta typically involves a trade-off between speed and accuracy. A common approach is to pick a reasonable value of eta and then stick with it for the rest of the tuning process. Let’s use eta = 0.1, because it uses about half as many steps as eta = 0.05, and the accuracy is comparable.
Grid Search
Sometimes it helps to tune a pair of related parameters together. A grid search runs through all possible combinations of candidate values for a selection of parameters.
We will tune the parameters max_depth and max_leaves together. These both affect the size the trees that the algorithm grows. Deeper trees with more leaves make the model more complex. We use the expand.grid function to store some reasonable candidate values in paramDF.
paramDF <- expand.grid(
max_depth = seq(15, 29, by = 2),
max_leaves = c(63, 127, 255, 511, 1023, 2047, 4095),
eta = 0.1)
If you View(paramDF) you can see that we have 56 different parameter choices to run through. The rest of the code is the same as before, but this loop might take a while to execute.
paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list)
bestResults <- tibble()
set.seed(312)
pb <- txtProgressBar(style = 3)
for(i in seq(length(paramList))) {
rwCV <- xgb.cv(params = paramList[[i]],
data = dtrain,
nrounds = 500,
nfold = 10,
early_stopping_rounds = 10,
verbose = FALSE)
bestResults <- bestResults %>%
bind_rows(rwCV$evaluation_log[rwCV$best_iteration])
gc()
setTxtProgressBar(pb, i/length(paramList))
}
close(pb)
depth_leaves <- bind_cols(paramDF, bestResults)
When we View(depth_leaves) we see that a choice of max_depth = 21 and max_leaves = 4095 results in the best test_rmse_mean. One caveat is that cross validation is a random process, so running this code with a different random seed may very well produce a different result. However, there are several comparable results with max_depth in the 20s and max_leaves in the 1000s, so we can be pretty sure that our choice these parameter values is sound.
Challenge: Write a Grid Search Function
Instead of repeatedly using the above code block, let’s package it into an R function. Define a function called
GridSearchthat consumes a data frameparamDFof candidate parameter values and anxgb.DMatrixdtrainof training data. The function should return a data frame combining the columns ofparamDFwith the corresponding results of the best cross validation iteration. The returned data frame should be sorted in ascending order oftest_rmse_mean.Solution
GridSearch <- function(paramDF, dtrain) { paramList <- lapply(split(paramDF, 1:nrow(paramDF)), as.list) bestResults <- tibble() pb <- txtProgressBar(style = 3) for(i in seq(length(paramList))) { rwCV <- xgb.cv(params = paramList[[i]], data = dtrain, nrounds = 500, nfold = 10, early_stopping_rounds = 10, verbose = FALSE) bestResults <- bestResults %>% bind_rows(rwCV$evaluation_log[rwCV$best_iteration]) gc() setTxtProgressBar(pb, i/length(paramList)) } close(pb) return(bind_cols(paramDF, bestResults) %>% arrange(test_rmse_mean)) }Check the function on a small example.
set.seed(630) GridSearch(tibble(eta = c(0.3, 0.2, 0.1)), dtrain)| | | 0% | |======================= | 33% | |=============================================== | 67% | |======================================================================| 100%# A tibble: 3 × 6 eta iter train_rmse_mean train_rmse_std test_rmse_mean test_rmse_std <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 0.1 100 0.220 0.00805 0.589 0.0543 2 0.2 40 0.256 0.0123 0.598 0.0426 3 0.3 41 0.170 0.00669 0.610 0.0468
Adding Random Sampling
Adding random sampling to the training process can help make the model less dependent on the training set, and hopefully more accurate when generalizing to future cases. In XGBoost, the two parameters subsample and colsample_bytree will grow trees based on a random sample of a specified percentage of rows and columns, respectively. Typical values for these parameters are between 0.5 and 1.0 (where 1.0 implies that no random sampling will be done).
Challenge: Tune Row and Column Sampling
Use a grid search to tune the parameters
subsampleandcolsample_bytree. Choose candidate values between 0.5 and 1.0. Use our previously chosen values ofeta,max_depth, andmax_leaves.Solution
paramDF <- expand.grid( subsample = seq(0.5, 1, by = 0.1), colsample_bytree = seq(0.5, 1, by = 0.1), max_depth = 21, max_leaves = 4095, eta = 0.1) set.seed(848) randsubsets <- GridSearch(paramDF, dtrain)It appears that some amount of randomization helps, but there are many choices for
subsampleandcolsample_bytreethat seem equivalent.
Final Check using the Testing Set
Once a model has been tuned using the training set and cross validation, it can be tested using the testing set. Note that we have not used the testing set in any of our tuning experiments, so the testing set accuracy should give a fair assessment of the accuracy of our tuned model relative to the other models we have explored.
We give parameters max_depth, max_leaves, subsample, and colsample_bytree the values that we chose during the tuning process. Since we only have to do one training run, a smaller learning rate won’t incur much of a time penalty, so we set eta = 0.05.
set.seed(805)
rwMod <- xgb.train(data = dtrain, verbose = 0,
watchlist = list(train = dtrain, test = dtest),
nrounds = 10000,
early_stopping_rounds = 50,
max_depth = 21,
max_leaves = 4095,
subsample = 0.8,
colsample_bytree = 0.7,
eta = 0.05)
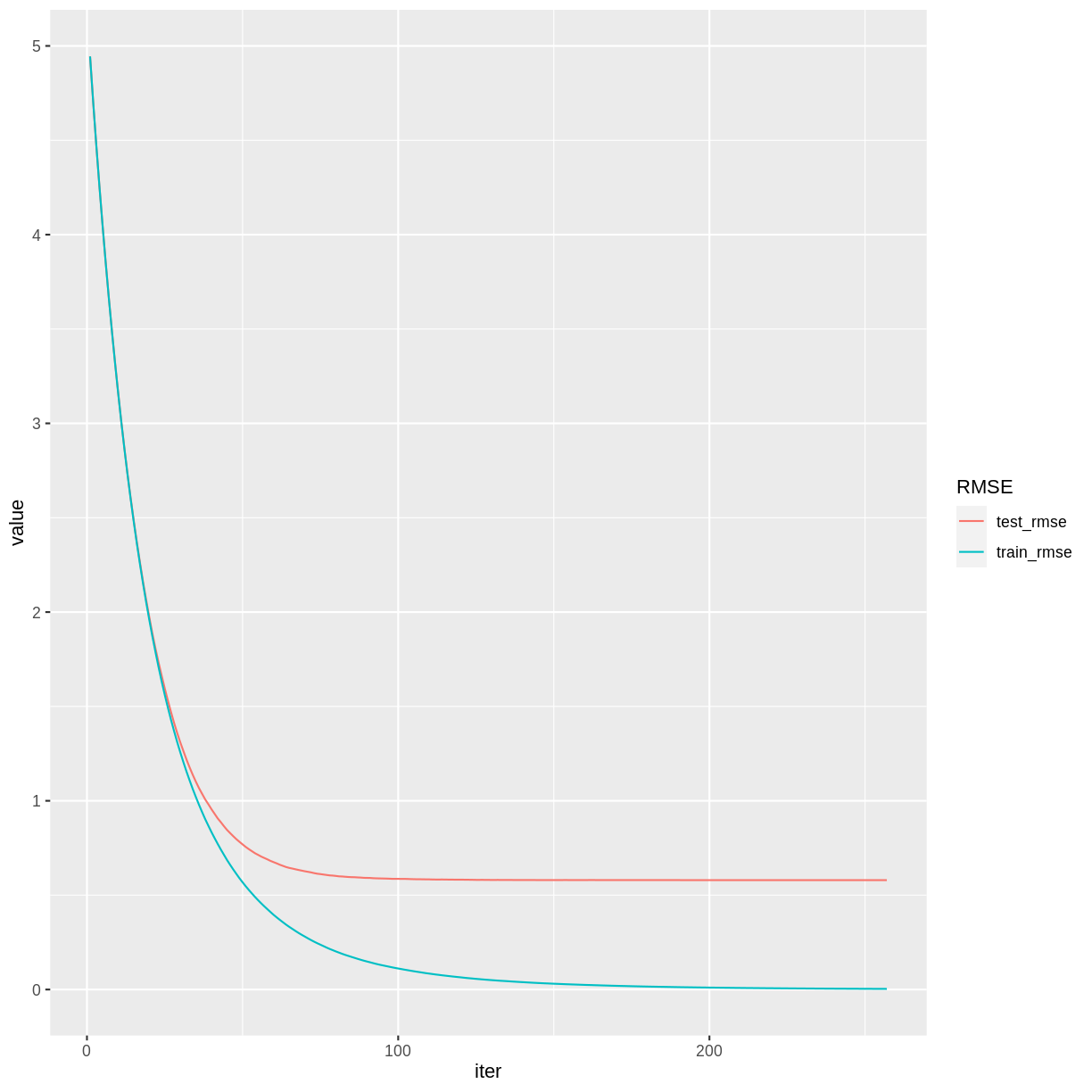
rwMod$evaluation_log %>%
pivot_longer(cols = c(train_rmse, test_rmse), names_to = "RMSE") %>%
ggplot(aes(x = iter, y = value, color = RMSE)) + geom_line()
print(rwMod)
##### xgb.Booster
raw: 5.9 Mb
call:
xgb.train(data = dtrain, nrounds = 10000, watchlist = list(train = dtrain,
test = dtest), verbose = 0, early_stopping_rounds = 50, max_depth = 21,
max_leaves = 4095, subsample = 0.8, colsample_bytree = 0.7,
eta = 0.05)
params (as set within xgb.train):
max_depth = "21", max_leaves = "4095", subsample = "0.8", colsample_bytree = "0.7", eta = "0.05", validate_parameters = "1"
xgb.attributes:
best_iteration, best_msg, best_ntreelimit, best_score, niter
callbacks:
cb.evaluation.log()
cb.early.stop(stopping_rounds = early_stopping_rounds, maximize = maximize,
verbose = verbose)
# of features: 11
niter: 257
best_iteration : 207
best_ntreelimit : 207
best_score : 0.579419
best_msg : [207] train-rmse:0.008751 test-rmse:0.579419
nfeatures : 11
evaluation_log:
iter train_rmse test_rmse
1 4.944344393 4.9445344
2 4.702804815 4.7020469
---
256 0.003205872 0.5795760
257 0.003140355 0.5795782
After some tuning, our testing set RMSE is down to 0.58, which is an improvement over the previous episode, and comparable to the RMSE we obtained using the random forest model.
Challenge: Improve the White Wine Model
Improve your XGBoost model for the white wine data (rows 1600-6497) of the
winedata frame. Use grid searches to tune several parameters, using only the training set during the tuning process. Can you improve the testing set RMSE over the white wine challenges from the previous two episodes?Solution
Results may vary. The proposed solution below will take quite some time to execute.
whitewine <- wine %>% dplyr::slice(1600:6497) trainSize <- round(0.80 * nrow(whitewine)) set.seed(1234) trainIndex <- sample(nrow(whitewine), trainSize) trainDF <- whitewine %>% dplyr::slice(trainIndex) testDF <- whitewine %>% dplyr::slice(-trainIndex) dtrain <- xgb.DMatrix(data = as.matrix(select(trainDF, -quality)), label = trainDF$quality) dtest <- xgb.DMatrix(data = as.matrix(select(testDF, -quality)), label = testDF$quality)Start by tuning
max_depthandmax_leavestogether.paramGrid <- expand.grid( max_depth = seq(10, 40, by = 2), max_leaves = c(15, 31, 63, 127, 255, 511, 1023, 2047, 4095, 8191), eta = 0.1 ) set.seed(1981) ww_depth_leaves <- GridSearch(paramGrid, dtrain)There are several options that perform similarly. Let’s choose
max_depth= 12 along withmax_leaves= 255. Now we tune the two random sampling parameters together.paramGrid <- expand.grid( subsample = seq(0.5, 1, by = 0.1), colsample_bytree = seq(0.5, 1, by = 0.1), max_depth = 12, max_leaves = 255, eta = 0.1 ) set.seed(867) ww_randsubsets <- GridSearch(paramGrid, dtrain)Again, some randomization seems to help, but there are several options. We’ll choose
subsample= 0.9 andcolsample_bytree= 0.6. Finally, we train the model with the chosen parameters.set.seed(5309) ww_gbmod <- xgb.train(data = dtrain, verbose = 0, watchlist = list(train = dtrain, test = dtest), nrounds = 10000, early_stopping_rounds = 50, max_depth = 12, max_leaves = 255, subsample = 0.9, colsample_bytree = 0.6, eta = 0.01)The tuned XGBoost model has a testing set RMSE of about 0.62, which is better than the un-tuned model from the last episode (0.66), and also better than the random forest model (0.63).
Key Points
Parameter tuning can improve the fit of an XGBoost model.
Cross validation allows us to tune parameters using the training set only, saving the testing set for final model evaluation.