Content from Introduction to Deep Learning
Last updated on 2024-05-30 | Edit this page
Overview
Questions
- What is machine learning and what is it used for?
- What is deep learning?
- How do I use a neural network for image classification?
Objectives
- Explain the difference between artificial intelligence, machine learning and deep learning.
- Understand the different types of computer vision tasks.
- Perform an image classification using a convolutional neural network (CNN).
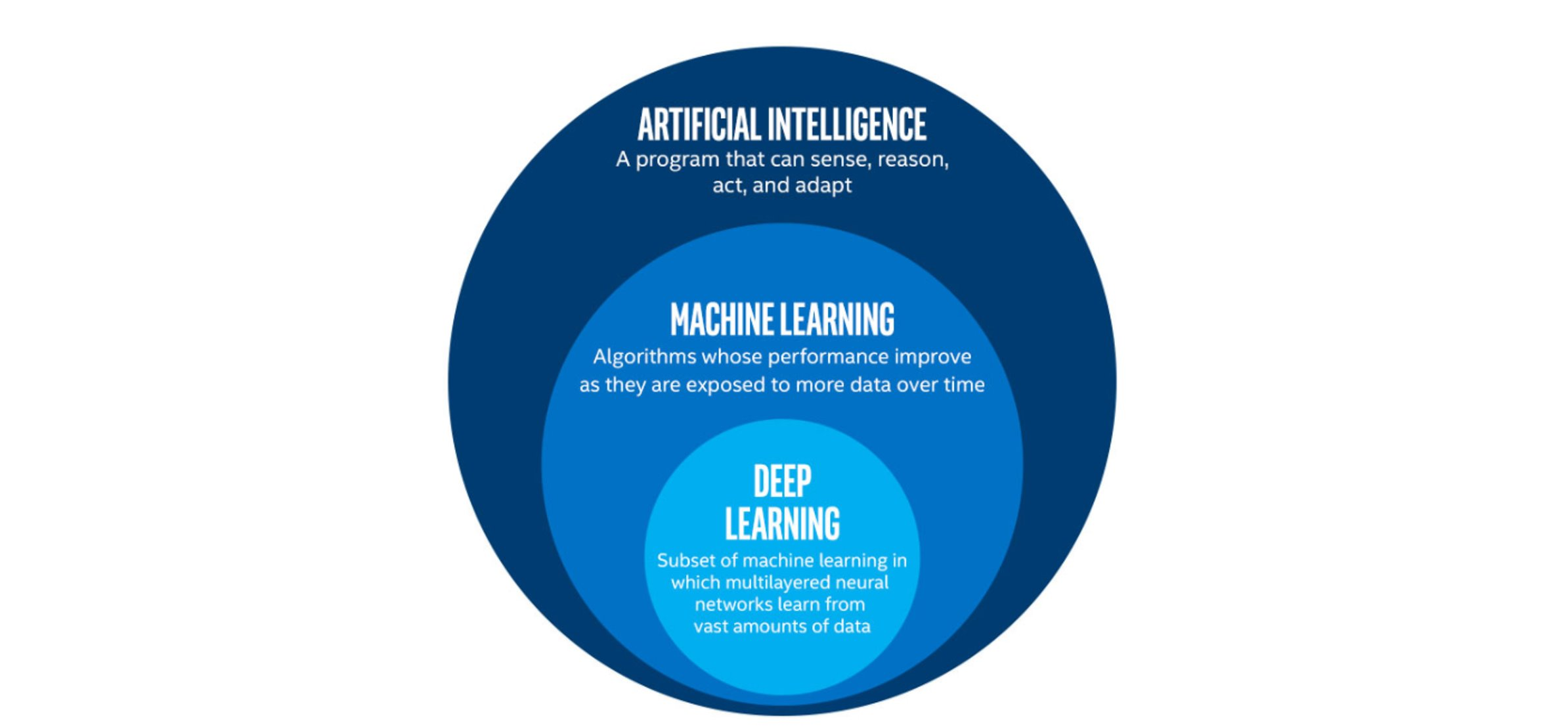
Deep Learning, Machine Learning and Artificial Intelligence
Artificial Intelligence (AI) is the broad field that involves creating machines capable of performing tasks that typically require human intelligence. This includes everything from recognizing speech and images to making decisions and translating languages. Within AI, Machine Learning (ML) is a subset focused on the development of algorithms that allow computers to learn and improve from experience without being explicitly programmed.
Deep Learning (DL), a further subset of ML, utilizes neural networks with many layers (hence “deep”) to model complex patterns in large amounts of data. This technique has led to significant advances in various fields, such as image and speech recognition.
Since the 1950s, the idea of AI has captured the imagination of many, often depicted in science fiction as machines with human-like or even superior intelligence. While recent advancements in AI and ML have been remarkable, we are currently capable of achieving human-like intelligence only in specific areas. The goal of creating a general-purpose AI, one that can perform any intellectual task a human can, remains a long-term challenge.
The image below illustrates some differences between artificial intelligence, machine learning and deep learning.
What is machine learning?
Machine learning is a set of tools and techniques which let us find patterns in data. The techniques break down into two broad categories, predictors and classifiers. Predictors are used to predict a value (or set of values) given a set of inputs whereas classifiers try to classify data into different categories, or assign a label.
Many, but not all, machine learning systems “learn” by taking a series of input data and output data and using it to form a model. The maths behind the machine learning doesn’t care what the data is as long as it can represented numerically or categorised. Some examples might include:
- Predicting a person’s weight based on their height.
- Predicting house prices given stock market prices.
- Classifying an email as spam or not.
- Classifying an image as, e.g., a person, place, or particular object.
Typically we train our models with hundreds, thousands or even millions of examples before they work well enough to do any useful predictions or classifications with them.
This lesson will introduce you to only one of these techniques, Deep Learning with Convolutional Neural Network, abbreviated as CNN, but there are many more.
A CNN is a DL algorithm that has become a cornerstone in image classification due to its ability to automatically learn features from images in a hierarchical fashion (i.e. each layer builds upon what was learned by the previous layer). It can achieve remarkable performance on a wide range of tasks.
What is image classification?
Image classification is a fundamental task in computer vision, which is a field of artificial intelligence focused on teaching computers to interpret and understand visual information from the world. Image classification specifically involves the process of assigning a label or category to an input image. The goal is to enable computers to recognise and categorise objects, scenes, or patterns within images, just as a human would. Image classification can refer to one of several computer vision tasks:
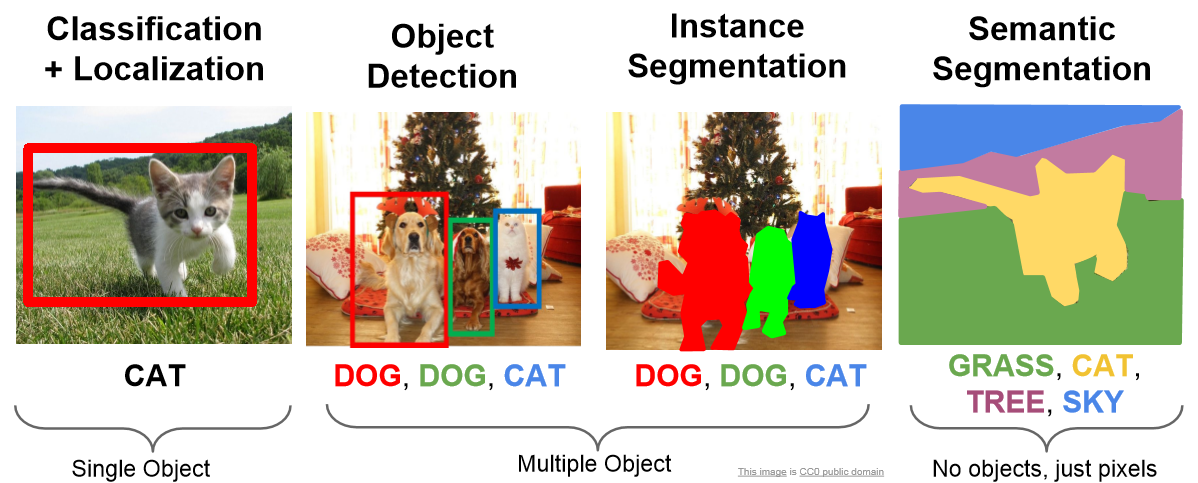
Image classification has numerous practical applications, including:
- Object Recognition: Identifying objects within images, such as cars, animals, or household items.
- Medical Imaging: Diagnosing diseases from medical images like X-rays or MRIs.
- Quality Control: Inspecting products for defects on manufacturing lines.
- Autonomous Vehicles: Identifying pedestrians, traffic signs, and other vehicles in self-driving cars.
- Security and Surveillance: Detecting anomalies or unauthorised objects in security footage.
Deep Learning Workflow
To apply Deep Learning to a problem there are several steps to go through:
Step 1. Formulate / Outline the problem
Firstly we must decide what it is we want our Deep Learning system to do. This lesson is all about image classification so our aim is to put an image into one of a few categories. Specifically in our case, we have 10 categories: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck
Step 2. Identify inputs and outputs
Next identify what the inputs and outputs of the neural network will be. In our case, the data is images and the inputs could be the individual pixels of the images. We are performing a classification problem and we will have one output for each potential class.
Step 3. Prepare data
Many datasets are not ready for immediate use in a neural network and will require some preparation. Neural networks can only really deal with numerical data, so any non-numerical data (e.g., images) will have to be somehow converted to numerical data. Information on how this is done and the data structure will be explored in Episode 02 Introduction to Image Data.
For this lesson, we will use an existing image dataset known as CIFAR-10 (Canadian Institute for Advanced Research). We will introduce the different data preparation tasks in more detail in the next episode but for this introduction, we will prepare the datset with these steps:
- normalise the image pixel values to be between 0 and 1
- one-hot encode the training image labels
- divide the data into training, validation, and test subsets
Preparing the code
It is the goal of this training workshop to produce a Deep Learning program, using a Convolutional Neural Network. At the end of this workshop, we hope this code can be used as a “starting point”. We will create an “initial program” for this introduction chapter that will be used as a foundation for the rest of the episodes.
Here’s one we prepared earlier!
To follow along in Spyder, Set the working directory to the ‘…/intro-image-classification-cnn/scripts’ folder where ‘…’ is your project folder.
PYTHON
# load the required packages
from tensorflow import keras # for neural networks
from sklearn.model_selection import train_test_split # for splitting data into sets
import matplotlib.pyplot as plt # for plotting
# create a function to prepare the training dataset
def prepare_dataset(train_images, train_labels):
# normalize the RGB values to be between 0 and 1
train_images = train_images / 255.0
# one hot encode the training labels
train_labels = keras.utils.to_categorical(train_labels, len(class_names))
# split the training data into training and validation set
train_images, val_images, train_labels, val_labels = train_test_split(
train_images, train_labels, test_size = 0.2, random_state=42)
return train_images, val_images, train_labels, val_labels
# load the data
(train_images, train_labels), (test_images, test_labels) = keras.datasets.cifar10.load_data()
# create a list of class names associated with each CIFAR-10 label
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
### Step 3. Prepare data
# prepare the dataset for training
train_images, val_images, train_labels, val_labels = prepare_dataset(train_images, train_labels)CHALLENGE Examine the CIFAR-10 dataset
OUTPUT
Train: Images=(40000, 32, 32, 3), Labels=(40000, 10)
Validate: Images=(10000, 32, 32, 3), Labels=(10000, 10)
Test: Images=(10000, 32, 32, 3), Labels=(10000, 1)The training set consists of 40000 images of 32x32 pixels and three channels (RGB values) and one-hot encoded labels.
The validation set consist of 10000 images of 32x32 pixels and three channels (RGB values) and one-hot encoded labels.
The test set consists of 10000 images of 32x32 pixels and three channels (RGB values) and labels.
Visualise a subset of the CIFAR-10 dataset
PYTHON
# set up plot region, including width, height in inches
fig, axes = plt.subplots(nrows=5, ncols=5, figsize=(10,10))
# add images to plot
for i,ax in enumerate(axes.flat):
ax.imshow(train_images[i])
ax.axis('off')
ax.set_title(class_names[train_labels[i,].argmax()])
# view plot
plt.show()
Step 4. Choose a pre-trained model or build a new architecture from scratch
Often we can use an existing neural network instead of designing one from scratch. Training a network can take a lot of time and computational resources. There are a number of well publicised networks which have been demonstrated to perform well at certain tasks. If you know of one which already does a similar task well, then it makes sense to use one of these.
If instead we decide to design our own network, then we need to think about how many input neurons it will have, how many hidden layers and how many outputs, and what types of layers to use. This will require some experimentation and tweaking of the network design a few times before achieving acceptable results.
Here we present an initial model to be explained in detail later on:
Define the Model
PYTHON
def create_model_intro():
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)
# create the model
model_intro = keras.Model(inputs = inputs_intro,
outputs = outputs_intro,
name = "cifar_model_intro")
return model_intro
# create the introduction model
model_intro = create_model_intro()
# view model summary
model_intro.summary()Step 5. Choose a loss function and optimizer and compile model
To set up a model for training we need to compile it. This is when you set up the rules and strategies for how your network is going to learn.
The loss function tells the training algorithm how far away the predicted value was from the true value. We will learn how to choose a loss function in more detail in Episode 4 Compile and Train (Fit) a Convolutional Neural Network.
The optimizer is responsible for taking the output of the loss function and then applying some changes to the weights within the network. It is through this process that “learning” (adjustment of the weights) is achieved.
Step 6. Train the model
We can now go ahead and start training our neural network. We will probably keep doing this for a given number of iterations through our training dataset (referred to as epochs) or until the loss function gives a value under a certain threshold.
PYTHON
# fit the model
history_intro = model_intro.fit(x = train_images, y = train_labels,
batch_size = 32,
epochs = 10,
validation_data = (val_images, val_labels))Your output will begin to print similar to the output below:
OUTPUT
Epoch 1/10
1250/1250 [==============================] - 15s 12ms/step - loss: 1.4651 - accuracy: 0.4738 - val_loss: 1.2736 - val_accuracy: 0.5507What does this output mean?
This output printed during the fit phase, i.e. training the model against known image labels, can be broken down as follows:
-
Epochdescribes the number of full passes over all training data. - `In the output above, there are 1250 batches
(steps) to complete each epoch.
- This number is calculated as the total number of images used as input divided by the batch size (40000/32). After 1250 batches, all training images will have been seen once and the model moves on to the next epoch.
-
lossis a value the model will attempt to minimise and is a measure of the dissimilarity or error between the true label of an image and the model prediction. Minimising this distance is where learning occurs to adjust weights and bias which reduceloss. -
val_lossis a value calculated against the validation data and is a measure of the model’s performance against unseen data.- Both values are a summation of errors made during each epoch.
-
accuracyandval_accuracyvalues are a percentage and are only revelant to classification problems.- The
val_accuracyscore can be used to communicate a model’s effectiveness on unseen data.
- The
Step 7. Perform a Prediction/Classification
After training the network we can use it to perform predictions. This is how you would use the network after you have fully trained it to a satisfactory performance. The predictions performed here on a special hold-out set is used in the next step to measure the performance of the network. Make sure the images you use to test are prepared the same way as the training images.
PYTHON
# normalize test dataset RGB values to be between 0 and 1
test_images = test_images / 255.0
# make prediction for the first test image
result_intro = model_intro.predict(test_images[0].reshape(1,32,32,3))
print(result_intro)
# extract class with highest probability
print(class_names[result_intro.argmax()])OUTPUT
1/1 [==============================] - 0s 93ms/step
[[0.00896197 0.00345764 0.20091638 0.3295959 0.3042777 0.03966621 0.06654432 0.00352677 0.03928733 0.00376582]]
catCongratulations, you just created your first image classification model and used it to classify an image!
Was the classification correct?
PYTHON
# plot the first test image with its true label
# create a plot
plt.figure()
# display image
plt.imshow(test_images[0])
plt.title('True class:' + class_names[result_intro.argmax()])
# view plot
plt.show() 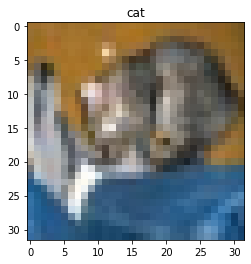
My result is different! Why? What can I do about?
This is actually not surprising. The architecture we are using is shallow and the model only trained for 10 epochs.
Training a model for more epochs (longer time) and using a deeper model (more layers) usually helps it learn better and give more accurate predictions. When a model has learned well and its performance doesn’t change much with more training, we say it has ‘converged.’ Convergence refers to the point where the model has reached an optimal or near-optimal state in terms of learning from the training data. If you are finding significant differences in the model predictions, this could be a sign the model is not fully converged.
You may even find you get a different answer if you run this model again. Although the neural network itself is deterministic (ie without randomness), various factors in the training process, system setup, and hardware configurations can lead to small variations in the output. These variations are usually minor and should not significantly impact the overall performance of the model, if it has fully converged.
There are many ways to try to improve the accuracy of our model, such as adding or removing layers to the model definition and fine-tuning the hyperparameters, which takes us to the next steps in our workflow.
Step 8. Measure Performance
Once we trained the network we want to measure its performance. To do this, we use additional data that was not part of the training, called a test dataset. There are many different methods available for measuring performance and which one is best depends on the type of task we are attempting. These metrics are often published as an indication of how well our network performs.
Step 9. Tune Hyperparameters
When building image recognition models in Python, especially using libraries like TensorFlow or Keras, the process involves not only designing a neural network but also choosing the best values for various hyperparameters that govern the training process.
Hyperparameters are all the parameters set by the person configuring the model as opposed to those learned by the algorithm itself. These hyperparameters can include the learning rate, the number of layers in the network, the number of neurons per layer, and many more. Hyperparameter tuning refers to the process of systematically searching for the best combination of hyperparameters that will optimise the model’s performance. This concept will be continued, with practical examples, in Episode 05 Evaluate a Convolutional Neural Network and Make Predictions (Classifications).
Step 10. Share Model
Once we have a trained network that performs at a level we are happy with we can use it to predict on real-world data. At this point we might want to consider publishing a file with both the architecture of our network and the weights which it has learned (assuming we did not use a pre-trained network). This will allow others to use it as as pre-trained network for their own purposes and for them to (mostly) reproduce our result.
To share the model we must save it first:
We will return to each of these workflow steps throughout this lesson and discuss each component in more detail.
- Machine learning is the process where computers learn to recognise patterns of data.
- Deep learning is a subset of machine learning, which is a subset of artificial intelligence.
- Convolutional neural networks are well suited for image classification.
- To use Deep Learning effectively we follow a workflow of: defining the problem, identifying inputs and outputs, preparing data, choosing the type of network, training the model, tuning hyperparameters, and measuring performance before we can classify data.
Content from Introduction to Image Data
Last updated on 2024-05-30 | Edit this page
Overview
Questions
- How much data do you need for Deep Learning?
- How do I prepare image data for use in a convolutional neural network (CNN)?
- How do I work with image data in python?
- Where can I find image data to train my model?
Objectives
- Understand the properties of image data.
- Write code to prepare an image dataset to train a CNN.
- Know the difference between training, testing, and validation datasets.
- Identify sources of image data.
Deep Learning Workflow
Let’s start over from the beginning of our workflow.
Step 1. Formulate/ Outline the problem
Firstly we must decide what it is we want our Deep Learning system to do. This lesson is all about image classification and our aim is to put an image into one of ten categories: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, or truck
Step 2. Identify inputs and outputs
Next we identify the inputs and outputs of the neural network. In our case, the data is images and the inputs could be the individual pixels of the images.
We are performing a classification problem and we want to output one category for each image.
Step 3. Prepare data
Deep Learning requires extensive training data which tells the network what output it should produce for a given input. In this workshop, our network will be trained on a series of images and told what they contain. Once the network is trained, it should be able to take another image and correctly classify its contents.
How much data do you need for Deep Learning?
Unfortunately, this question is not easy to answer. It depends, among other things, on the complexity of the task (which you often do not know beforehand), the quality of the available dataset and the complexity of the network. For complex tasks with large neural networks, adding more data often improves performance. However, this is also not a generic truth: if the data you add is too similar to the data you already have, it will not give much new information to the neural network.
In case you have too little data available to train a complex network from scratch, it is sometimes possible to use a pretrained network that was trained on a similar problem. Another trick is data augmentation, where you expand the dataset with artificial data points that could be real. An example of this is mirroring images when trying to classify cats and dogs. An horizontally mirrored animal retains the label, but exposes a different view.
Depending on your situation, you will prepare your own custom data for training or use pre-existing data.
Custom image data
In some cases, you will create your own set of labelled images.
The steps to prepare your own custom image data include:
Custom data i. Data collection and Labeling:
For image classification the label applies to the entire image; object detection requires bounding boxes around objects of interest, and instance or semantic segmentation requires each pixel to be labelled.
There are a number of open source software used to label your dataset, including:
- (Visual Geometry Group) VGG Image Annotator (VIA)
- ImageJ can be extended with plugins for annotation
- COCO Annotator is designed specifically for creating annotations compatible with Common Objects in Context (COCO) format
Custom data ii. Data preprocessing:
This step involves various tasks to enhance the quality and consistency of the data:
Resizing: Resize images to a consistent resolution to ensure uniformity and reduce computational load.
Augmentation: Apply random transformations (e.g., rotations, flips, shifts) to create new variations of the same image. This helps improve the model’s robustness and generalisation by exposing it to more diverse data.
Normalisation: Scale pixel values to a common range, often between 0 and 1 or -1 and 1. Normalisation helps the model converge faster during training.
Label encoding is a technique used to represent categorical data with numerical labels.
Data Splitting: Split the data set into separate parts to have one for training, one for evaluating the model’s performance during training, and one reserved for the final evaluation of the model’s performance.
Before jumping into these specific preprocessing tasks, it’s important to understand that images on a computer are stored as numerical representations or simplified versions of the real world. Therefore it’s essential to take some time to understand these numerical abstractions.
Pixels
Images on a computer are stored as rectangular arrays of hundreds, thousands, or millions of discrete “picture elements,” otherwise known as pixels. Each pixel can be thought of as a single square point of coloured light.
For example, consider this image of a Jabiru, with a square area designated by a red box:

Now, if we zoomed in close enough to the red box, the individual pixels would stand out:

Note each square in the enlarged image area (i.e. each pixel) is all one colour, but each pixel can be a different colour from its neighbours. Viewed from a distance, these pixels seem to blend together to form the image.
Working with Pixels
In python, an image can represented as a 2- or 3-dimensional array. An array is used to store multiple values or elements of the same datatype in a single variable. In the context of images, arrays have dimensions for height, width, and colour channels (if applicable) and each element corresponds to a pixel value in the image. Let us start with the Jabiru image.
PYTHON
# specify the image path
new_img_path = "../data/Jabiru_TGS.JPG"
# read in the image with default arguments
new_img_pil = keras.utils.load_img(path=new_img_path)
# check the image class and size
print('Image class :', new_img_pil.__class__)
print('Image size:', new_img_pil.size)OUTPUT
Image class : <class 'PIL.JpegImagePlugin.JpegImageFile'>
Image size (552, 573)Image Dimensions - Resizing
The new image has shape (573, 552), meaning it is much
larger in size, 573x552 pixels and is a rectangle instead of a
square.
Recall from the introduction that our training data set consists of 50000 images of 32x32 pixels.
To reduce the computational load and ensure all of our images have a uniform size, we need to choose an image resolution (or size in pixels) and ensure all of the images we use are resized to be consistent.
There are a couple of ways to do this in python but one way is to
specify the size you want using the target_size argument to
the keras.utils.load_img() function.
PYTHON
# read in the image and specify the target size
new_img_pil_small = keras.utils.load_img(path=new_img_path, target_size=(32,32))
# confirm the image class and size
print('Resized image class :', new_img_pil_small.__class__)
print('Resized image size', new_img_pil_small.size) OUTPUT
Resized image class : <class 'PIL.Image.Image'>
Resized image size (32, 32)Of course, if there are a large number of images to preprocess you do not want to copy and paste these steps for each image! Fortunately, Keras has a solution: keras.utils.image_dataset_from_directory()
Two of the most commonly used libraries for image representation and manipulation are NumPy and Pillow (PIL). Additionally, when working with deep learning frameworks like TensorFlow and PyTorch, images are often represented as tensors within these frameworks.
- NumPy is a powerful library for numerical computing in Python. It
provides support for creating and manipulating arrays, which can be used
to represent images as multidimensional arrays.
import numpy as np
- The Pillow library provides functions to open, manipulate, and save
various image file formats. It represents images using its own Image
class.
from PIL import Image- PIL Image Module documentation
- TensorFlow images are often represented as tensors that have
dimensions for batch size, height, width, and colour channels. This
framework provide tools to load, preprocess, and work with image data
seamlessly.
from tensorflow import keras- image preprocessing documentation
- Note Keras image functions also use PIL
Image augmentation
There are several ways to augment your data to increase the diversity of the training data and improve model robustness.
- Geometric Transformations
- rotation, scaling, zooming, cropping
- Flipping or Mirroring
- some classes, like horse, have a different shape when facing left or right and you want your model to recognize both
- Colour properties
- brightness, contrast, or hue
- these changes simulate variations in lighting conditions
We will not perform image augmentation in this lesson, but it is important that you are aware of this type of data preparation because it can make a big difference in your model’s ability to predict outside of your training data.
Information about these operations are included in the Keras document for Image augmentation layers.
Normalisation
Image RGB values are between 0 and 255. As input for neural networks, it is better to have small input values. The process of converting the RGB values to be between 0 and 1 is called normalisation.
Before we can normalise our image values we must convert the image to an numpy array.
We introduced how to do this in Episode 01 Introduction to Deep Learning
but what you may not have noticed is that the
keras.datasets.cifar10.load_data() function did the
conversion for us whereas now we will do it ourselves.
PYTHON
# first convert the image into an array for normalisation
new_img_arr = keras.utils.img_to_array(new_img_pil_small)
# confirm the image class and shape
print('Converted image class :', new_img_arr.__class__)
print('Converted image shape', new_img_arr.shape)OUTPUT
Converted image class : <class 'numpy.ndarray'>
Converted image shape (32, 32, 3)Now that the image is an array, we can normalise the values. Let us also investigate the image values before and after we normalise them.
PYTHON
# inspect pixel values before and after normalisation
# extract the min, max, and mean pixel values BEFORE
print('BEFORE normalisation')
print('Min pixel value ', new_img_arr.min())
print('Max pixel value ', new_img_arr.max())
print('Mean pixel value ', new_img_arr.mean().round())
# normalise the RGB values to be between 0 and 1
new_img_arr_norm = new_img_arr / 255.0
# extract the min, max, and mean pixel values AFTER
print('AFTER normalisation')
print('Min pixel value ', new_img_arr_norm.min())
print('Max pixel value ', new_img_arr_norm.max())
print('Mean pixel value ', new_img_arr_norm.mean().round())OUTPUT
BEFORE normalisation
Min pixel value 0.0
Max pixel value 255.0
Mean pixel value 87.0
AFTER normalisation
Min pixel value 0.0
Max pixel value 1.0
Mean pixel value 0.0ChatGPT
Normalizing the RGB values to be between 0 and 1 is a common pre-processing step in machine learning tasks, especially when dealing with image data. This normalisation has several benefits:
Numerical Stability: By scaling the RGB values to a range between 0 and 1, you avoid potential numerical instability issues that can arise when working with large values. Neural networks and many other machine learning algorithms are sensitive to the scale of input features, and normalizing helps to keep the values within a manageable range.
Faster Convergence: Normalizing the RGB values often helps in faster convergence during the training process. Neural networks and other optimisation algorithms rely on gradient descent techniques, and having inputs in a consistent range aids in smoother and faster convergence.
Equal Weightage for All Channels: In RGB images, each channel (Red, Green, Blue) represents different colour intensities. By normalizing to the range [0, 1], you ensure that each channel is treated with equal weightage during training. This is important because some machine learning algorithms could assign more importance to larger values.
Generalisation: Normalisation helps the model to generalize better to unseen data. When the input features are in the same range, the learned weights and biases can be more effectively applied to new examples, making the model more robust.
Compatibility: Many image-related libraries, algorithms, and models expect pixel values to be in the range of [0, 1]. By normalizing the RGB values, you ensure compatibility and seamless integration with these tools.
The normalisation process is typically done by dividing each RGB value (ranging from 0 to 255) by 255, which scales the values to the range [0, 1].
For example, if you have an RGB image with pixel values (100, 150, 200), after normalisation, the pixel values would become (100/255, 150/255, 200/255) ≈ (0.39, 0.59, 0.78).
Remember that normalisation is not always mandatory, and there could be cases where other scaling techniques might be more suitable based on the specific problem and data distribution. However, for most image-related tasks in machine learning, normalizing RGB values to [0, 1] is a good starting point.
One-hot encoding
A neural network can only take numerical inputs and outputs, and learns by calculating how “far away” the class predicted by the neural network is from the true class. When the target (label) is categorical data, or strings, it is very difficult to determine this “distance” or error. Therefore we will transform this column into a more suitable format. There are many ways to do this, however we will be using one-hot encoding.
One-hot encoding is a technique to represent categorical data as binary vectors, making it compatible with machine learning algorithms. Each category becomes a separate column, and the presence or absence of a category is indicated by 1s and 0s in the respective columns.
Let’s say you have a dataset with a “colour” column containing three categories: yellow, orange, purple.
Table 1. Original Data.
| colour | |
|---|---|
| yellow | 🟨 |
| orange | 🟧 |
| purple | 🟪 |
| yellow | 🟨 |
Table 2. After One-Hot Encoding.
| colour_yellow | colour_orange | colour_purple |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
The Keras function for one_hot encoding is called to_categorical:
keras.utils.to_categorical(y, num_classes=None, dtype="float32")
-
yis an array of class values to be converted into a matrix (integers from 0 to num_classes - 1). -
num_classesis the total number of classes. If None, this would be inferred as max(y) + 1. -
dtypeis the data type expected by the input. Default: ‘float32’
Data Splitting
The typical practice in machine learning is to split your data into two subsets: a training set and a test set. This initial split separates the data you will use to train your model (Step 6) from the data you will use to evaluate its performance (Step 8).
After this initial split, you can choose to further split the training set into a training set and a validation set. This is often done when you are fine-tuning hyperparameters, selecting the best model from a set of candidate models, or preventing overfitting.
To split a dataset into training and test sets there is a very convenient function from sklearn called train_test_split:
sklearn.model_selection.train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)
- The first two parameters are the dataset (X) and the corresponding targets (y) (i.e. class labels).
-
test_sizeis the fraction of the dataset used for testing -
random_statecontrols the shuffling of the dataset, setting this value will reproduce the same results (assuming you give the same integer) every time it is called. -
shufflecontrols whether the order of the rows of the dataset is shuffled before splitting and can be eitherTrueorFalse. -
stratifyis a more advanced parameter that controls how the split is done.
Pre-existing image data
In other cases you will be able to download an image dataset that is already labelled and can be used to classify a number of different object like the CIFAR-10 dataset. Other examples include:
- MNIST database - 60,000 training images of handwritten digits (0-9)
- ImageNet - 14 million hand-annotated images indicating objects from more than 20,000 categories. ImageNet sponsors an annual software contest where programs compete to achieve the highest accuracy. When choosing a pretrained network, the winners of these sorts of competitions are generally a good place to start.
- MS COCO - >200,000 labelled images used for object detection, instance segmentation, keypoint analysis, and captioning
Where labelled data exists, in most cases the data provider or other users will have created data-specific functions you can use to load the data. We already did this in the introduction:
PYTHON
from tensorflow import keras
# load the CIFAR-10 dataset included with the keras library
(train_images, train_labels), (test_images, test_labels) = keras.datasets.cifar10.load_data()
# create a list of classnames associated with each CIFAR-10 label
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']In this instance the data is likely already prepared for use in a CNN. However, it is always a good idea to first read any associated documentation to find out what steps the data providers took to prepare the images and second to take a closer at the images once loaded and query their attributes.
In our case, we still want prepare the dataset with these steps:
- normalise the image pixel values to be between 0 and 1
- one-hot encode the training image labels
- divide the training data into training and validation sets
We performed these operations in Step 3. Prepare data of the Introduction but let us create the function to prepare the dataset again knowing what we know now.
CHALLENGE Create a function to prepare the dataset
Hint 1: Your function should accept the training images and labels as arguments
Hint 2: Use 20% split for validation and a random state of ‘42’
PYTHON
def prepare_dataset(train_images, train_labels):
# normalise the RGB values to be between 0 and 1
train_images = train_images / 255
# one hot encode the training labels
train_labels = keras.utils.to_categorical(train_labels, len(class_names))
# split the training data into training and validation set
train_images, val_images, train_labels, val_labels = train_test_split(
train_images, train_labels, test_size = 0.2, random_state=42)
return train_images, val_images, train_labels, val_labelsInspect the labels before and after data preparation to visualise one-hot encoding.
PYTHON
print()
print('train_labels before one hot encoding')
print(train_labels)
# prepare the dataset for training
train_images, val_images, train_labels, val_labels = prepare_dataset(train_images, train_labels)
print()
print('train_labels after one hot encoding')
print(train_labels)OUTPUT
train_labels before one hot encoding
[[6]
[9]
[9]
...
[9]
[1]
[1]]
train_labels after one hot encoding
[[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 1.]
[0. 0. 0. ... 0. 0. 1.]
...
[0. 0. 0. ... 0. 0. 1.]
[0. 1. 0. ... 0. 0. 0.]
[0. 1. 0. ... 0. 0. 0.]]WAIT I thought there were TEN classes!? Where is the rest of the data?
The Spyder IDE uses the ‘…’ notation when it “hides” some of the data for display purposes.
To view the entire array, go the Variable Explorer in the upper right hand corner of your Spyder IDE and double click on the ‘train_labels’ object. This will open a new window that shows all of the columns.
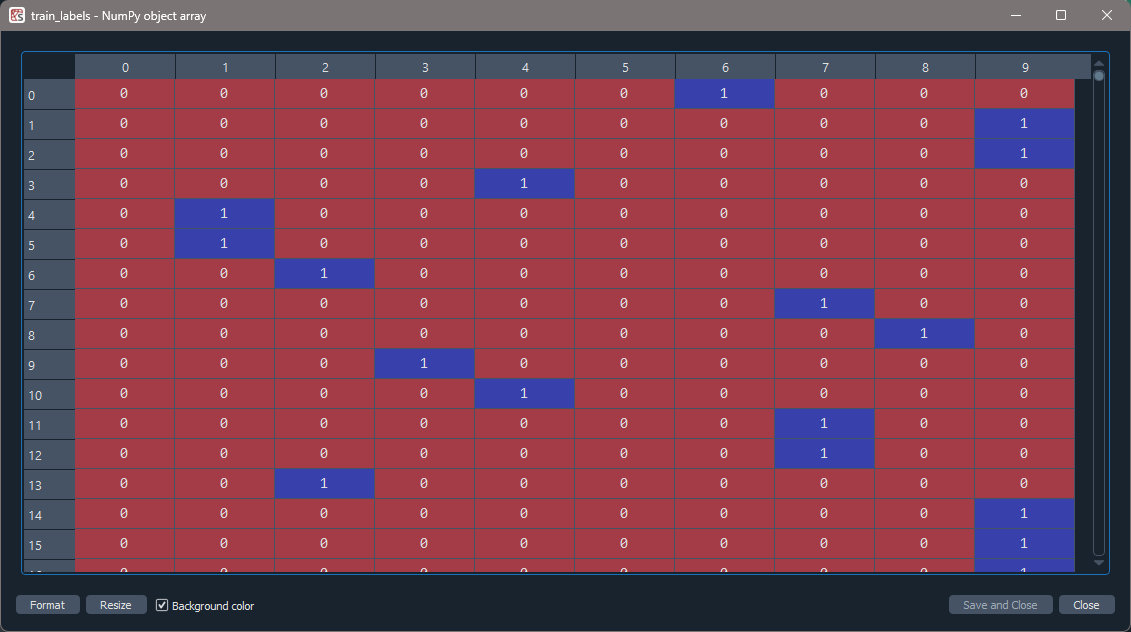
CHALLENGE Training and Validation
Inspect the training and validation sets we created.
How many samples does each set have and are the classes well balanced?
Hint: Use np.sum() on the ’*_labels’ to find out if the
classes are well balanced.
A. Training Set
PYTHON
print('Number of training set images', train_images.shape[0])
print('Number of images in each class:\n', train_labels.sum(axis=0))OUTPUT
Number of training set images: 40000
Number of images in each class:
[4027. 4021. 3970. 3977. 4067. 3985. 4004. 4006. 3983. 3960.]B. Validation Set (we can use the same code as the training set)
PYTHON
print('Number of validation set images', val_images.shape[0])
print('Nmber of images in each class:\n', val_labels.sum(axis=0))OUTPUT
Number of validation set images: 10000
Nmber of images in each class:
[ 973. 979. 1030. 1023. 933. 1015. 996. 994. 1017. 1040.]ChatGPT
Data is typically split into the training, validation, and test data sets using a process called data splitting or data partitioning. There are various methods to perform this split, and the choice of technique depends on the specific problem, dataset size, and the nature of the data. Here are some common approaches:
Hold-Out Method:
In the hold-out method, the dataset is divided into two parts initially: a training set and a test set.
The training set is used to train the model, and the test set is kept completely separate to evaluate the model’s final performance.
This method is straightforward and widely used when the dataset is sufficiently large.
Train-Validation-Test Split:
The dataset is split into three parts: the training set, the validation set, and the test set.
The training set is used to train the model, the validation set is used to tune hyperparameters and prevent overfitting during training, and the test set is used to assess the final model performance.
This method is commonly used when fine-tuning model hyperparameters is necessary.
K-Fold Cross-Validation:
In k-fold cross-validation, the dataset is divided into k subsets (folds) of roughly equal size.
The model is trained and evaluated k times, each time using a different fold as the test set while the remaining k-1 folds are used as the training set.
The final performance metric is calculated as the average of the k evaluation results, providing a more robust estimate of model performance.
This method is particularly useful when the dataset size is limited, and it helps in better utilizing available data.
Stratified Sampling:
Stratified sampling is used when the dataset is imbalanced, meaning some classes or categories are underrepresented.
The data is split in such a way that each subset (training, validation, or test) maintains the same class distribution as the original dataset.
This ensures all classes are well-represented in each subset, which is important to avoid biased model evaluation.
It’s important to note that the exact split ratios (e.g., 80-10-10 or 70-15-15) may vary depending on the problem, dataset size, and specific requirements. Additionally, data splitting should be performed randomly to avoid introducing any biases into the model training and evaluation process.
Data preprocessing completed!
We now have a function we can use throughout the lesson to preprocess our data which means we are ready to learn how to build a CNN like we used in the introduction.
- Image datasets can be found online or created uniquely for your research question.
- Images consist of pixels arranged in a particular order.
- Image data is usually preprocessed before use in a CNN for efficiency, consistency, and robustness.
- Input data generally consists of three sets: a training set used to fit model parameters; a validation set used to evaluate the model fit on training data; a test set used to evaluate the final model performance.
Content from Build a Convolutional Neural Network
Last updated on 2024-05-30 | Edit this page
Overview
Questions
- What is a (artificial) neural network (ANN)?
- How is a convolutional neural network (CNN) different from an ANN?
- What are the types of layers used to build a CNN?
Objectives
- Understand how a convolutional neural network (CNN) differs from an artificial neural network (ANN).
- Explain the terms: kernel, filter.
- Know the different layers: convolutional, pooling, flatten, dense.
Neural Networks
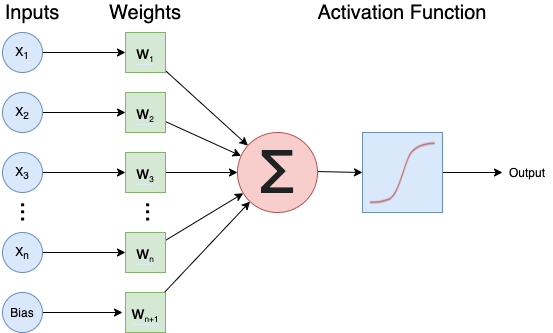
A neural network is an artificial intelligence technique loosely based on the way neurons in the brain work.
A single neuron
Each neuron will:
- Take one or more inputs (\(x_1, x_2, ...\)), e.g., floating point numbers, each with a corresponding weight.
- Calculate the weighted sum of the inputs where ($w_1, w_2, … $) indicate weights.
- Add an extra constant weight (i.e. a bias term) to this weighted sum.
- Apply a non-linear function to the bias-adjusted weighted sum.
- Return one output value, again a floating point number.
One example equation to calculate the output for a neuron is:
\(output=ReLU(∑i(xi∗wi)+bias)\)
Combining multiple neurons into a network
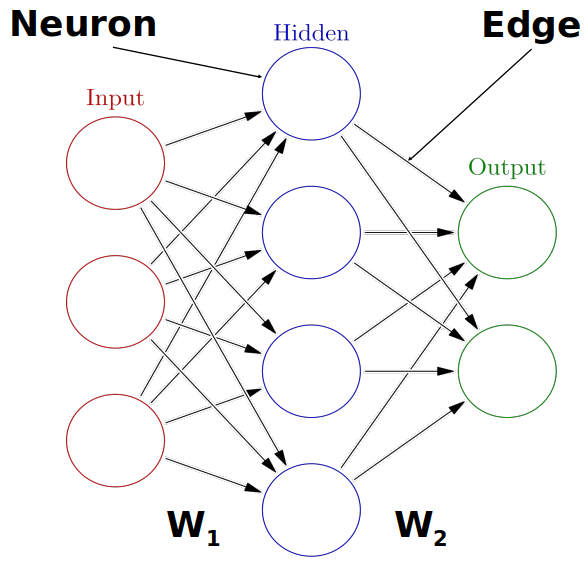
Multiple neurons can be joined together by connecting the output of one to the input of another. These connections are also associated with weights that determine the ‘strength’ of the connection, and these weights are also adjusted during training. In this way, the combination of neurons and connections describe a computational graph, an example can be seen in the image below.
In most neural networks neurons are aggregated into layers. Signals travel from the input layer to the output layer, possibly through one or more intermediate layers called hidden layers. The image below illustrates an example of a neural network with three layers, each circle is a neuron, each line is an edge and the arrows indicate the direction data moves in.
Neural networks aren’t a new technique, they have been around since the late 1940s. But until around 2010 neural networks tended to be quite small, consisting of only 10s or perhaps 100s of neurons. This limited them to only solving quite basic problems. Around 2010 improvements in computing power and the algorithms for training the networks made much larger and more powerful networks practical. These are known as deep neural networks or Deep Learning.
Convolutional Neural Networks
A convolutional neural network (CNN) is a type of artificial neural network (ANN) most commonly applied to analyze visual imagery. They are specifically designed for processing grid-like data, such as images, by leveraging convolutional layers that preserve spatial relationships, when extracting features.
Step 4. Build an architecture from scratch or choose a pretrained model
Let us explore how to build a neural network from scratch. Although this sounds like a daunting task, with Keras it is surprisingly straightforward. With Keras you compose a neural network by creating layers and linking them together.
Parts of a neural network
There are three main components of a neural network:
- CNN Part 1. Input Layer
- CNN Part 2. Hidden Layers
- CNN Part 3. Output Layer
The output from each layer becomes the input to the next layer.
CNN Part 1. Input Layer
The Input in Keras gets special treatment when images are used. Keras
automatically calculates the number of inputs and outputs a specific
layer needs and therefore how many edges need to be created. This means
we just need to let Keras know how big our input is going to be. We do
this by instantiating a keras.Input class and passing it a
tuple to indicate the dimensionality of the input data. In Python, a
tuple is a data type used to store collections of data.
It is similar to a list, but tuples are immutable, meaning once they are
created, their contents cannot be changed.
The input layer is created with the keras.Input function
and its first parameter is the expected shape of the input:
keras.Input(shape=None, batch_size=None, dtype=None, sparse=None, batch_shape=None, name=None, tensor=None)In our case, the shape of an image is defined by its pixel dimensions and number of channels:
OUTPUT
(40000, 32, 32, 3) # number of images, image width in pixels, image height in pixels, number of channels (RGB)CHALLENGE Create the input layer for our network
Hint 1: Specify shape argument only and use defaults for the rest.
Hint 2: The shape of our input dataset includes the total number of images. We want to take a slice of the shape for a single individual image to use an input.
OUTPUT
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])CNN Part 2. Hidden Layers
The next component consists of the so-called hidden layers of the network.
In a neural network, the input layer receives the raw data, and the output layer produces the final predictions or classifications. These layers’ contents are directly observable because you can see the input data and the network’s output predictions.
However, the hidden layers, which lie between the input and output layers, contain intermediate representations of the input data. These representations are transformed through various mathematical operations performed by the network’s neurons. The specific values and operations within these hidden layers are not directly accessible or interpretable from the input or output data. Therefore, they are considered “hidden” from external observation or inspection.
In a CNN, the hidden layers typically consist of convolutional, pooling, reshaping (e.g., Flatten), and dense layers.
Check out the Layers API section of the Keras documentation for each layer type and its parameters.
Convolutional Layers
A convolutional layer is a fundamental building block in a CNN designed for processing structured, gridded data, such as images. It applies convolution operations to input data using learnable filters or kernels, extracting local patterns and features (e.g. edges, corners). These filters enable the network to capture hierarchical representations of visual information, allowing for effective feature learning.
To find the particular features of an image, CNNs make use of a concept from image processing that precedes Deep Learning.
A convolution matrix, or kernel, is a matrix transformation that we ‘slide’ over the image to calculate features at each position of the image. For each pixel, we calculate the matrix product between the kernel and the pixel with its surroundings. Here is one example of a 3x3 kernel used to detect edges:
[[-1, -1, -1],
[0, 0, 0]
[1, 1, 1]]This kernel will give a high value to a pixel if it is on a horizontal border between dark and light areas.
In the following image, the effect of such a kernel on the values of a single-channel image stands out. The red cell in the output matrix is the result of multiplying and summing the values of the red square in the input, and the kernel. Applying this kernel to a real image demonstrates it does indeed detect horizontal edges.
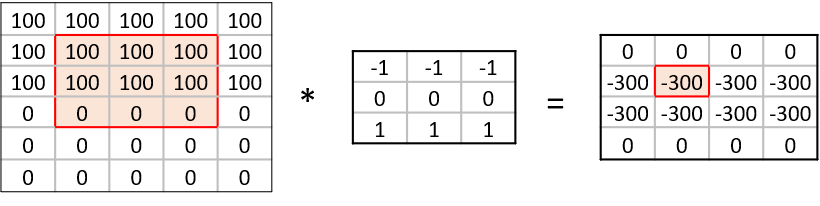
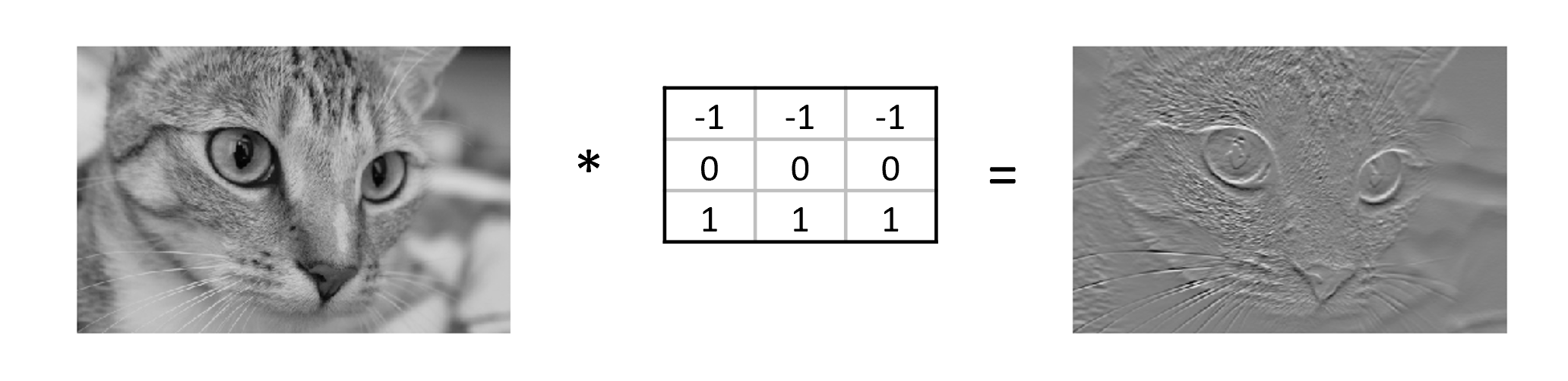
There are several types of convolutional layers available in Keras depending on your application. We use the two-dimensional layer typically used for images:
keras.layers.Conv2D(filters, kernel_size, strides=(1, 1), padding="valid", activation=None, **kwargs)-
filtersis the number of filters in this layer.- This is one of the hyperparameters of our system and should be chosen carefully.
- Good practice is to start with a relatively small number of filters in the first layer to prevent overfitting.
- Choosing a number of filters as a power of two (e.g., 32, 64, 128) is common.
-
kernel sizeis the size of the convolution matrix which we already discussed. - Smaller kernels are often used to capture fine-grained features and odd-sized filters are preferred because they have a centre pixel which helps maintain spatial symmetry during convolutions. -
activationspecifies which activation function to use.
When specifying layers, remember each layer’s output is the input to the next layer. We must create a variable to store a reference to the output so we can pass it to the next layer. The basic format for doing this is:
output_variable = layer_name(layer_arguments)(input_variable)
CHALLENGE Create a 2D convolutional layer for our network
Create a Conv2D layer with 16 filters, a 3x3 kernel size, and the ‘relu’ activation function.
Here we choose relu which is one of the most
commonly used in deep neural networks that is proven to work well. We
will discuss activation functions later in Step 9. Tune
hyperparameters but to satisfy your curiosity,
ReLU stands for Rectified Linear Unit (ReLU).
Hint 1: The input to each layer is the output of the previous layer.
OUTPUT
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)Playing with convolutions
Convolutions applied to images can be hard to grasp at first. Fortunately, there are resources out there that enable users to interactively play around with images and convolutions:
Image kernels explained illustrates how different convolutions can achieve certain effects on an image, like sharpening and blurring.
The convolutional neural network cheat sheet provides animated examples of the different components of convolutional neural nets.
Pooling Layers
The convolutional layers are often intertwined with Pooling layers. As opposed to the convolutional layer used in feature extraction, the pooling layer alters the dimensions of the image and reduces it by a scaling factor effectively decreasing the resolution of your picture.
The rationale behind this is that higher layers of the network should focus on higher-level features of the image. By introducing a pooling layer, the subsequent convolutional layer has a broader ‘view’ on the original image.
Similar to convolutional layers, Keras offers several pooling layers and one used for images (2D spatial data):
keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, padding="valid", data_format=None, name=None, **kwargs)-
pool_size, i.e., the size of the pooling window- In Keras, the default is usually (2, 2)
The function downsamples the input along its spatial dimensions (height and width) by taking the maximum value over an input window (of size defined by pool_size) for each channel of the input. By taking the maximum instead of the average, the most prominent features in the window are emphasized.
For example, a 2x2 pooling size reduces the width and height of the input by a factor of 2. Empirically, a 2x2 pooling size has been found to work well in various for image classification tasks and also strikes a balance between down-sampling for computational efficiency and retaining important spatial information.
OUTPUT
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)Dense layers
A dense layer is a fully connected layer where each neuron receives input from every neuron in the previous layer. When connecting the layer to its input and output layers every neuron in the dense layer gets an edge (i.e. connection) to all of the input neurons and all of the output neurons.
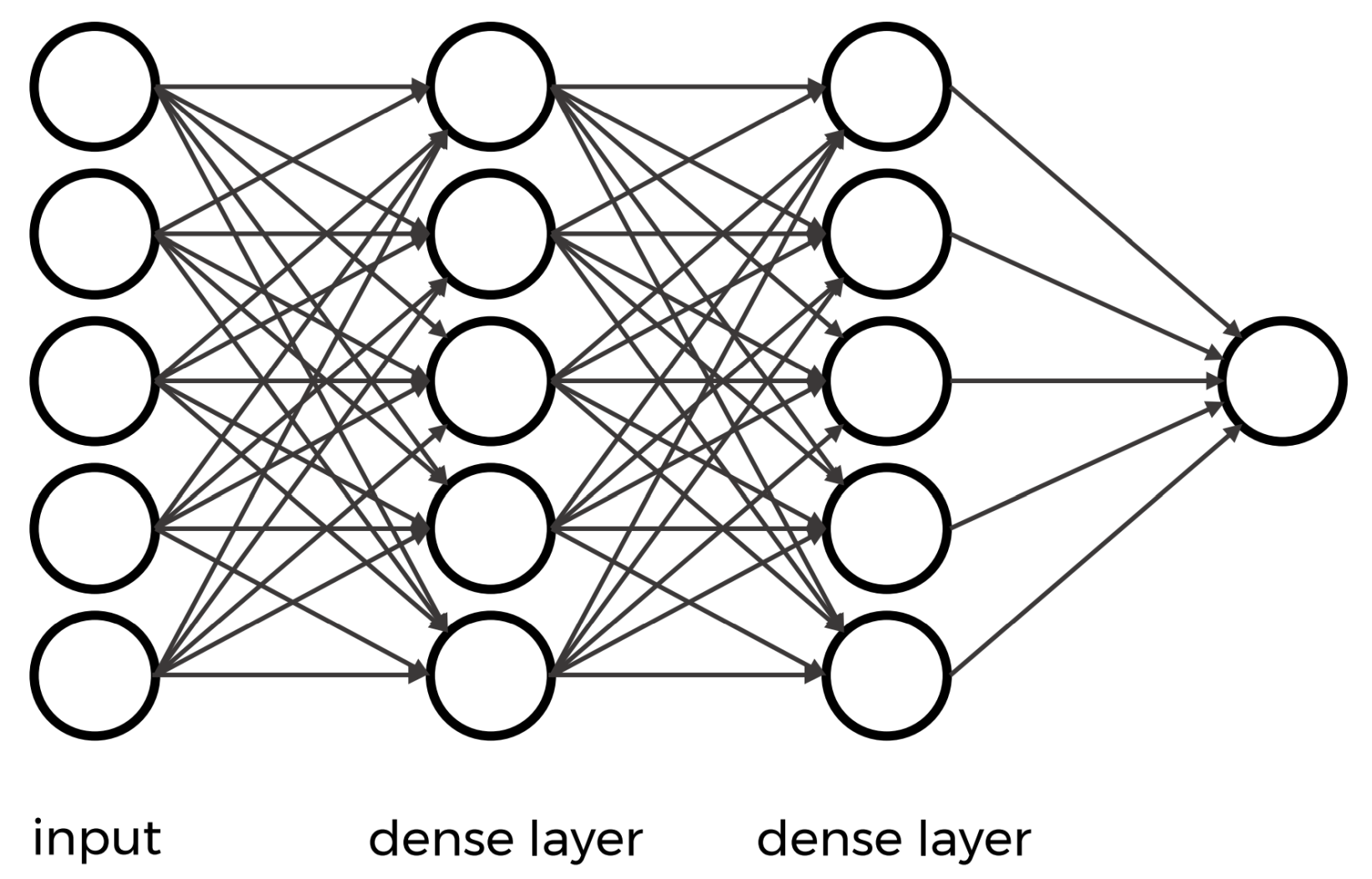
This layer aggregates global information about the features learned in previous layers to make a decision about the class of the input.
In Keras, a densely-connected layer is defined:
keras.layers.Dense(units, activation=None, **kwargs)- `units in this case refers to the number of neurons.
The choice of how many neurons to specify is often determined through experimentation and can impact the performance of our CNN. Too few neurons may not capture complex patterns in the data but too many neurons may lead to overfitting.
OUTPUT
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)Reshaping Layers: Flatten
The next type of hidden layer used in our introductory model is a
type of reshaping layer defined in Keras by the
keras.layers.Flatten class. It is necessary when
transitioning from convolutional and pooling layers to fully connected
layers.
keras.layers.Flatten(data_format=None, **kwargs)The Flatten layer converts the output of the previous layer into a single one-dimensional vector that can be used as input for a dense layer.
OUTPUT
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)A flatten layer function is typically used to transform the two-dimensional arrays (matrices) generated by the convolutional and pooling layers into a one-dimensional array. This is necessary when transitioning from the convolutional/pooling layers to the fully connected layers, which require one-dimensional input.
During the convolutional and pooling operations, a neural network extracts features from the input images, resulting in multiple feature maps, each represented by a matrix. These feature maps capture different aspects of the input image, such as edges, textures, or patterns. However, to feed these features into a fully connected layer for classification or regression tasks, they must be a single vector.
The flatten layer takes each element from the feature maps and arranges them into a single long vector, concatenating them along a single dimension. This transformation preserves the spatial relationships between the features in the original image while providing a suitable format for the fully connected layers to process.
Is one layer of each type enough?
Not for complex data!
A typical architecture for image classification is likely to include at least one convolutional layer, one pooling layer, one or more dense layers, and possibly a flatten layer.
Convolutional and Pooling layers are often used together in multiple sets to capture a wider range of features and learn more complex representations of the input data. Using this technique, the network can learn a hierarchical representation of features, where simple features detected in early layers are combined to form more complex features in deeper layers.
There isn’t a strict rule of thumb for the number of sets of convolutional and pooling layers to start with, however, there are some guidelines.
We are starting with a relatively small and simple architecture because we are limited in time and computational resources. A simple CNN with one or two sets of convolutional and pooling layers can still achieve decent results for many tasks but for your network you will experiment with different architectures.
OUTPUT
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)CNN Part 3. Output Layer
Recall for the outputs we asked ourselves what we want to identify from the data. If we are performing a classification problem, then typically we have one output for each potential class.
In traditional CNN architectures, a dense layer is typically used as the final layer for classification. This dense layer receives the flattened feature maps from the preceding convolutional and pooling layers and outputs the final class probabilities or regression values.
For multiclass data, the softmax activation is used
instead of relu because it helps the computer give each
option (class) a likelihood score, and the scores add up to 100 per
cent. This way, it’s easier to pick the one the computer thinks is most
probable.
CHALLENGE Create an Output layer for our network
Use a dense layer to create the output layer for a classification problem with 10 possible classes.
Hint 1: The input to each layer is the output of the previous layer.
Hint 2: The units (neurons) should be the same as number of classes as our dataset.
Hint 3: Use softmax activation.
OUTPUT
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)Putting it all together
Once you decide on the initial architecture of your CNN, the last
step to create the model is to bring all of the parts together using the
keras.Model class.
There are several ways of grouping the layers into an object as described in the Keras Models API.
We will use the Functional API to create our model using the inputs and outputs defined in this episode.
keras.Model(inputs=inputs, outputs=outputs)Note that there is additional argument that can be passed to the keras.Model class called ‘name’ that takes a string. Although it is no longer specified in the documentation, the ‘name’ argument is useful when deciding among different architectures.
CHALLENGE Create a function that defines an introductory CNN
Using the keras.Model class and the input, hidden, and output layers from the previous challenges, create a function that returns the CNN from the introduction.
Hint 1: Name the model “cifar_model_intro”
OUTPUT
def create_model_intro():
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)
# create the model
model_intro = keras.Model(inputs = inputs_intro,
outputs = outputs_intro,
name = "cifar_model_intro")
return model_introWe now have a function that defines the introduction model.
We can use this function to create the introduction model and and
view a summary of its structure using the Model.summary
method.
PYTHON
# create the introduction model
model_intro = create_model_intro()
# view model summary
model_intro.summary()OUTPUT
Model: "cifar_model_intro"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
conv2d (Conv2D) (None, 30, 30, 16) 448
max_pooling2d (MaxPooling2 (None, 15, 15, 16) 0
D)
conv2d_1 (Conv2D) (None, 13, 13, 32) 4640
max_pooling2d_1 (MaxPoolin (None, 6, 6, 32) 0
g2D)
flatten (Flatten) (None, 1152) 0
dense (Dense) (None, 64) 73792
dense_1 (Dense) (None, 10) 650
=================================================================
Total params: 79530 (310.66 KB)
Trainable params: 79530 (310.66 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________The Model.summary() output has three columns:
- Layer (type) lists the name and type of each layer.
- Remember the ‘name’ argument we used to name our model? This argument can also be supplied to each layer. If a name is not provided, Keras will assign a unique identifier starting from 1 and incrementing for each new layer of the same type within the model.
- Output Shape describes the shape of the output produced by each
layer as (batch_size, height, width, channels).
- Batch size is the number of samples processed in each batch during training or inference. This dimension is often denoted as None in the summary because the batch size can vary and is typically specified during model training or inference.
- Height, Width, Channels: The remaining dimensions represent the spatial dimensions and the number of channels in the output tensor. For convolutional layers and pooling layers, the height and width dimensions typically decrease as the network progresses through the layers due to the spatial reduction caused by convolution and pooling operations. The number of channels may change depending on the number of filters in the convolutional layer or the design of the network architecture.
- For example, in a convolutional layer, the output shape (None, 30,
30, 16) means:
- None: The batch size can vary.
- 30: The height and width of the output feature maps are both 30 pixels.
- 16: There are 16 channels in the output feature maps, indicating that the layer has 16 filters.
- Param # displays the number of parameters (weights and biases)
associated with each layer.
- The total number of parameters in a layer is calculated as follows:
- Total parameters = (number of input units) × (number of output units) + (number of output units)
- At the bottom of the Model.summary() you will find the number of
Total parameters and their size; the number of Trainable parameters and
their size; and the number of Non-trainable parameters and their size.
- In most cases, the total number of parameters will match the number of trainable parameters. In other cases, such as models using normalization layers, there will be some parameters that are fixed during training and not trainable.
- Disclaimer: We explicitly decided to focus on building a foundational understanding of convolutional neural networks for this course without delving into the detailed calculation of parameters. However, as your progress on your deep learning journey it will become increasingly important for you to understand parameter calculation in order to optimize model performance, troubleshoot issues, and design more efficient CNN architectures.
- The total number of parameters in a layer is calculated as follows:
How to choose an architecture?
For this neural network, we had to make many choices, including the number of hidden neurons. Other choices to be made are the number of layers and type of layers. You might wonder how you should make these architectural choices. Unfortunately, there are no clear rules to follow here, and it often boils down to a lot of trial and error. It is recommended to explore what others have done with similar data sets and problems. Another best practice is to start with a relatively simple architecture and then add layers and tweak the network to test if performance increases.
We have a model now what?
This CNN should be able to run with the CIFAR-10 data set and provide reasonable results for basic classification tasks. However, do keep in mind this model is relatively simple, and its performance may not be as high as more complex architectures. The reason it’s called deep learning is because, in most cases, the more layers we have, i.e. the deeper and more sophisticated CNN architecture we use, the better the performance.
How can we judge a model’s performance? We can inspect a couple metrics produced during the training process to detect whether our model is underfitting or overfitting. To do that, we continue with the next steps in our Deep Learning workflow, Step 5. Choose a loss function and optimizer and Step 6. Train model.
- Artificial neural networks (ANN) are a machine learning technique based on a model inspired by groups of neurons in the brain.
- Convolution neural networks (CNN) are a type of ANN designed for image classification and object detection.
- The number of filters corresponds to the number of distinct features the layer is learning to recognise whereas the kernel size determines the level of features being captured.
- A CNN can consist of many types of layers including convolutional, pooling, flatten, and dense (fully connected) layers
- Convolutional layers are responsible for learning features from the input data.
- Pooling layers are often used to reduce the spatial dimensions of the data.
- The flatten layer is used to convert the multi-dimensional output of the convolutional and pooling layers into a flat vector.
- Dense layers are responsible for combining features learned by the previous layers to perform the final classification.
Content from Compile and Train (Fit) a Convolutional Neural Network
Last updated on 2024-05-20 | Edit this page
Overview
Questions
- How do you compile a convolutional neural network (CNN)?
- What is a loss function?
- What is an optimizer?
- How do you train (fit) a CNN?
- How do you evaluate a model during training?
- What is overfitting?
Objectives
- Explain the difference between compiling and training (fitting) a CNN.
- Know how to select a loss function for your model.
- Understand what an optimizer is.
- Define the terms: learning rate, batch size, epoch.
- Understand what loss and accuracy are and how to monitor them during training.
- Explain what overfitting is and what to do about it.
Step 5. Choose a loss function and optimizer and compile model
We have designed a convolutional neural network (CNN) that in theory we should be able to train to classify images.
We now need to compile the model, or set up the rules and strategies for how the network will learn. To do this, we select an appropriate loss function and optimizer to use during training (fitting).
The Keras method to compile a model is found in the Model training APIs section of the documentation and has the following structure:
Model.compile(
optimizer="rmsprop",
loss=None,
loss_weights=None,
metrics=None,
weighted_metrics=None,
run_eagerly=False,
steps_per_execution=1,
jit_compile="auto",
auto_scale_loss=True,
)The three arguments we want to set for this method are for the optimizer, the loss, and the metrics parameters.
Optimizer
An optimizer in this case refers to the algorithm with which the model learns to optimize on the provided loss function, or minimise the model error. In other words, the optimizer is responsible for taking the output of the loss function and then applying some changes to the weights within the network. It is through this process that the “learning” (adjustment of the weights) is achieved.
We need to choose an optimizer and, if this optimizer has parameters, decide what values to use for those. Similar to other hyperparameters, the choice of optimizer depends on the problem you are trying to solve, your model architecture, and your data.
Adam
Here we picked one of the most common optimizers demonstrated to work well for most tasks, the Adam optimizer, as our starting point.
In Keras, Adam is defined by the keras.optimizers.Adam
class:
keras.optimizers.Adam(
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-07,
amsgrad=False,
weight_decay=None,
clipnorm=None,
clipvalue=None,
global_clipnorm=None,
use_ema=False,
ema_momentum=0.99,
ema_overwrite_frequency=None,
loss_scale_factor=None,
gradient_accumulation_steps=None,
name="adam",
**kwargs
)As you can see, the Adam optimizer defines many parameters. For this introductory course, we will accept the default arguments but we highly recommend you investigate all of them if you decide to use this optimizer for your project.
For now, though, we do want to highlight the first parameter.
The Learning rate is a hyperparameter that determines the step size at which the model’s weights are updated during training. You can think of this like the pace of learning for your model because it’s basically how big (or small) a step your model takes to learn from its mistakes. Too high, and it might overshoot the optimal values; too low, and it might take forever to learn.
The learning rate may be fixed and remain constant throughout the entire training process or it may be adaptive and dynamically change during training.
The Keras optimizer documentation describes the other optimizers available to choose from. A couple more popular or famous ones include:
Stochastic Gradient Descent (sgd): Stochastic Gradient Descent (SGD) is one of the fundamental optimization algorithms used to train machine learning models, especially neural networks. It is a variant of the gradient descent algorithm, designed to handle large datasets efficiently.
-
Root Mean Square (rms)prop: RMSprop is widely used in various deep learning frameworks and is one of the predecessors of more advanced optimizers like Adam, which further refines the concept of adaptive learning rates. It is an extension of the basic Stochastic Gradient Descent (SGD) algorithm and addresses some of the challenges of SGD.
- For example, one of the main issues with the basic SGD is that it uses a fixed learning rate for all model parameters throughout the training process. This fixed learning rate can lead to slow convergence or divergence (over-shooting) in some cases. RMSprop introduces an adaptive learning rate mechanism to address this problem.
ChatGPT
Learning rate is a hyperparameter that determines the step size at which the model’s parameters are updated during training. A higher learning rate allows for more substantial parameter updates, which can lead to faster convergence, but it may risk overshooting the optimal solution. On the other hand, a lower learning rate leads to smaller updates, providing more cautious convergence, but it may take longer to reach the optimal solution. Finding an appropriate learning rate is crucial for effectively training machine learning models.
The figure below illustrates how a small learning rate will not traverse toward the minima of the gradient descent algorithm in a timely manner, i.e. number of epochs.

On the other hand, specifying a learning rate that is too high will result in a loss value that never approaches the minima. That is, ‘bouncing between the sides’, thus never reaching a minima to cease learning.

Finally, a modest learning rate will ensure that the product of multiplying the scalar gradient value and the learning rate does not result in too small steps, nor a chaotic bounce between sides of the gradient where steepness is greatest.

These images were obtained from Google Developers Machine Learning Crash Course and is licenced under the Creative Commons 4.0 Attribution Licence.
Loss function
The loss function tells the training algorithm how wrong, or how ‘far away’ from the true value, the predicted value is. The purpose of loss functions is to compute the quantity that a model should seek to minimize during training. Which class of loss functions you choose depends on your task.
Loss for classification
For classification purposes, there are a number of probabilistic
losses to choose from. Here we chose
CategoricalCrossentropy because we want to compute the
difference between our one-hot encoded class labels and the model
predictions and this loss function is appropriate when the data has two
or more label classes.
It is defined by the
keras.losses.CategoricalCrossentropy class:
keras.losses.CategoricalCrossentropy(
from_logits=False,
label_smoothing=0.0,
axis=-1,
reduction="sum_over_batch_size",
name="categorical_crossentropy",
)More information about loss functions can be found in the Keras loss documentation.
Metrics
After we select the desired optimizer and loss function we specify the metric(s) to be evaluated by the model during training and testing. A metric is a function used to judge the performance of the model.
Metric functions are similar to loss functions, except the results from evaluating a metric are not used when training the model. Note you can also use any loss function as a metric. The Keras metrics documentation provides a list of potential metrics.
Typically, for classification problems, you will use
CategoricalAccuracy, which calculates how often the model
predictions match the true labels, and in Keras is defined as:
keras.metrics.CategoricalAccuracy(name="categorical_accuracy", dtype=None)The accuracy function creates two local variables, total and count, that it uses to compute the frequency with which predictions matches labels. This frequency is ultimately returned as accuracy: an operation that divides the total by count.
Now that we selected which optimizer, loss function, and metric to use, we want to compile the model, or prepare it for training.
CHALLENGE Write the code to compile the introductory model
OUTPUT
# compile the model
model_intro.compile(optimizer = keras.optimizers.Adam(),
loss = keras.losses.CategoricalCrossentropy(),
metrics = keras.metrics.CategoricalAccuracy())Step 6. Train (Fit) model
We are ready to train the model.
Training a model means teaching the computer to recognize patterns in data by adjusting its internal parameters, or iteratively comparing its predictions with the actual outcomes to minimize errors. The result is a model capable of making accurate predictions on new, unseen data.
Training the model is done using the Model.fit
method:
Model.fit(
x=None,
y=None,
batch_size=None,
epochs=1,
verbose="auto",
callbacks=None,
validation_split=0.0,
validation_data=None,
shuffle=True,
class_weight=None,
sample_weight=None,
initial_epoch=0,
steps_per_epoch=None,
validation_steps=None,
validation_batch_size=None,
validation_freq=1,
)For this introductory course, the arguments we will specify are x, y, batch_size, epochs, and validation data.
- x refers to the input data, which in our case is the training data
- y refers to the target data, which in our case is the corresponding image labels
-
batch size determines the number of training
samples processed together before updating the model’s parameters during
each iteration (or mini-batch) of training.
- Choosing the right batch size depends on various factors, including your memory constraints, the model complexity, computational resources, and trial and error!
- In general, smaller batch sizes may require more iterations to cover the entire dataset, which can lead to longer training times. Larger batch sizes contribute to a smoother learning process, i.e. more consistent updates to the model’s parameters, but might not generalise well to new, unseen data.
- In practice, common sizes range from 32 to 256.
-
epochs In one epoch, every sample in the training
data will be given to the neural network and used to update its
parameters.
- In general, CNN models improve with more epochs of training, but only to a point.
- validation_data is the data used to evaluate loss and model metrics at the end of each epoch. The model will not be trained on this data.
The Model.fit method returns a History
object that records the training loss values and metrics. If we want to
keep this data, we need to create a new variable to capture the
return.
The weights and biases learned during the training process are stored directly within the model object itself.
Other parameters used to fit our model can be found in the documentation for the Keras fit method.
CHALLENGE Write the code to fit the introductory model
Use the Model.fit function to train (fit) the
model_intro.
Hint 1: Use a batch size of 32.
Hint 2: Train for 10 epochs.
Hint 3: Use a tuple of the form (x_val, y_val) and our validation dataset variable names.
Hint 4: Store the training loss and metrics in a variable call ‘history_intro’
OUTPUT
# fit the model
history_intro = model_intro.fit(x = train_images, y = train_labels,
batch_size = 32,
epochs = 10,
validation_data = (val_images, val_labels))ChatGPT
The choice of batch size can have various implications, and there are situations where using different batch sizes can be beneficial. There is no one-size-fits-all answer.
Large Datasets and Memory Constraints: If you have a large dataset and limited memory, using a smaller batch size can help fit the data into memory during training. This allows you to train larger models or use more complex architectures that might not fit with larger batch sizes.
Training on GPUs: Modern deep learning frameworks and libraries are optimized for parallel processing on GPUs. Using larger batch sizes can fully leverage the parallelism of GPUs and lead to faster training times. However, the choice of batch size should consider the available GPU memory.
Noise in Parameter Updates: Smaller batch sizes introduce more noise in the gradients, which can help models escape sharp minima and potentially find better solutions. This regularization effect is similar to the impact of stochasticity in Stochastic Gradient Descent (SGD).
Generalization: Using smaller batch sizes may improve the generalization of the model. It prevents the model from overfitting to the training data, as it gets updated more frequently and experiences more diverse samples during training.
It’s essential to consider the trade-offs of using different batch sizes. While larger batch sizes may provide more stable gradients during training, there could be a trade-off where the model might not generalise as effectively to new, unseen data. It’s a common consideration in machine learning to find a balance between stable training and the ability to generalize well to diverse examples. You should experiment with different batch sizes to find the best-performing one for your specific model, architecture, and dataset.
Before moving on, let us quickly save our model object.
We will discuss this method in more detail in Episode 6 Share a Convolutional Neural Network and Next Steps but for now just copy and paste.
Monitor Training Progress (aka Model Evaluation during Training)
We now know more about the compilation and fitting of CNNs and have a
trained model. How do we know if it is any good? We can inspect the
training metrics we stored in our History object.
Using seaborn, a Python data visualization library based on matplotlib that provides a high-level interface for drawing attractive and informative statistical graphics, we can plot the training process using the history:
PYTHON
import seaborn as sns
import pandas as pd
# convert the model history to a dataframe for plotting
history_intro_df = pd.DataFrame.from_dict(history_intro.history)
# plot the loss and accuracy from the training process
fig, axes = plt.subplots(1, 2)
fig.suptitle('cifar_model_intro')
sns.lineplot(ax=axes[0], data=history_intro_df[['loss', 'val_loss']])
sns.lineplot(ax=axes[1], data=history_intro_df[['categorical_accuracy', 'val_categorical_accuracy']])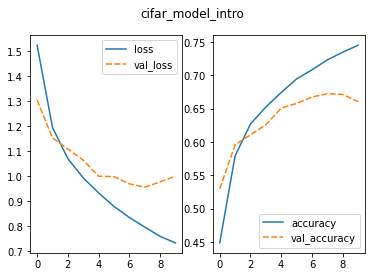
This plot is used to identify whether the training is well configured or whether there are problems to address. The solid blue lines represent the training loss and accuracy; the dashed orange lines represent the validation loss and accuracy.
CHALLENGE Inspect the Training Curve
Inspect the training curves we have just made and recall the difference between the training and the validation datasets.
- How does the training progress look?
- Does the loss increase or decrease?
- What about the accuracy?
- Do either change fast or slowly?
- Do the graphs lines fluctuate or go up and down frequently?
- Do you think the resulting trained network will work well on the test set?
- Key things to look for for:
- Loss
- The loss curve should drop quickly in a relatively smooth line with little to no fluctuations.
- The val_loss curve should decrease along with the loss.
- Accuracy
- The accuracy should increase quickly in a relatively smooth line with little to no fluctuations.
- The val_accuracy should behave similarly
- Loss
- The results of the training give very little information on its performance on a test set. You should be careful not to use it as an indication of a well trained network.
Note the training loss continues to decrease, while the validation loss stagnates, and even starts to increase over the course of the epochs. Similarly, the accuracy for the validation set does not improve anymore after some epochs.
This is evidence of overfitting in these plots. If a model is overfitting, it means the model performs exceptionally well on the training data, but poorly on the validation data. Overfitting occurs when the model has learned to memorize the noise and specific patterns in the training data instead of generalizing the underlying relationships. As a result, the model fails to perform well on new, unseen, data because it has become too specialized to the training set.
Key characteristics of an overfit model include:
High Training Accuracy, Low Validation Accuracy: The model achieves high accuracy on the training data but significantly lower accuracy on the validation (or test) data.
Small Training Loss, Large Validation Loss: The training loss is low, indicating the model’s predictions closely match the true labels in the training set. However, the validation loss is high, indicating the model’s predictions are far from the true labels in the validation set.
How to Address Overfitting:
- Reduce the model’s complexity by using fewer layers or units to make it less prone to overfitting.
- Collect more training data if possible to provide the model with a diverse and representative dataset.
- Perform data augmentation to artificially increase the size of the training data and introduce variability.
Underfitting occurs when the model is too simple or lacks the capacity to capture the underlying patterns and relationships present in the data. As a result, the model’s predictions are not accurate, and it fails to generalize well to unseen data.
Key characteristics of an underfit model include:
- Large Training Loss: The training loss (error) is high, indicating the model’s predictions are far from the true labels in the training set.
- Increasing validation loss.
- Low Validation Accuracy: This indicates the model is not learning from the data effectively.
How to address underfitting:
- Perform data augmentation or feature engineering to provide the model with more informative input features.
- Train the model for more epochs to give it more time to learn from the data.
- Increase the model’s complexity by adding more layers or units to the existing layers.
Improve Model Generalization (avoid Overfitting)
Techniques to avoid overfitting, or to improve model generalization, are termed regularization techniques. A short list of some of these include batch normalization, data augmentation, and dropout.
Dropout
One of the most versatile regularization technique is dropout (Srivastava et al., 2014). Dropout essentially means that during each training cycle a random fraction of the dense layer nodes are turned off. This is described with the dropout rate between zero and one, which determines the fraction of nodes to silence at a time.
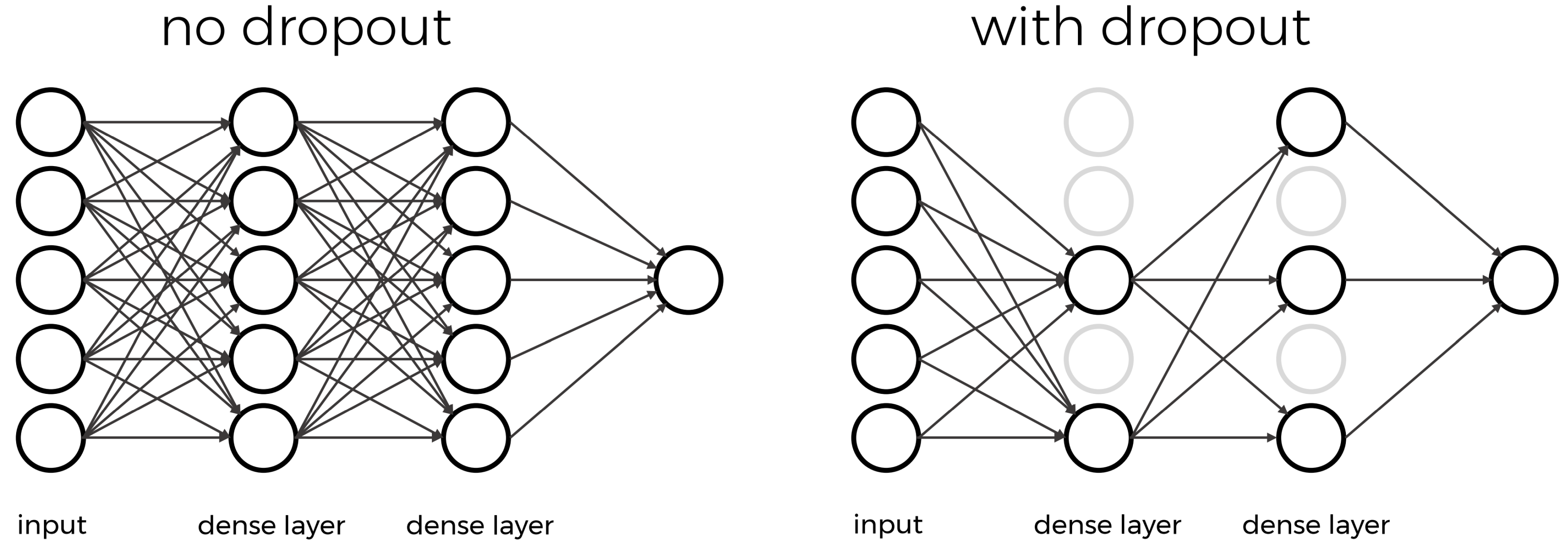
The intuition behind dropout is that it enforces redundancies in the network by constantly removing different elements of a network. The model can no longer rely on individual nodes and instead must create multiple “paths”.
In addition, the model has to make predictions with much fewer nodes and weights (connections between the nodes). As a result, it becomes much harder for a network to memorize particular features. At first this might appear a quite drastic approach which affects the network architecture strongly. In practice, however, dropout is computationally a very elegant solution which does not affect training speed. And it frequently works very well.
Dropout layers will only randomly silence nodes during training! During the prediction step, all nodes remain active (dropout is off). During training, the sample of nodes that are silenced are different for each training instance, or batch, to give all nodes a chance to observe enough training data to learn its weights.
Dropout layers are defined by the keras.layers.Dropout
class and have the following definition:
keras.layers.Dropout(rate, noise_shape=None, seed=None, **kwargs)- The
rateparameter is a float between 0 and 1 and represents the fraction of the input units to drop.- Good advice is to begin with a small dropout rate, such as 0.1 or 0.2, and gradually increase it if necessary.
- A dropout rate of 0.5 is commonly used as a starting point.
The placement of the dropout layer also matters because adding dropout before or after certain layers can have different effects. Although dropout layers are commonly added between dense layers, you will find network architectures with dropout in just about everywhere. Be sure to experiment with different dropout rates and placements to find the optimal configuration for your model and dataset.
CHALLENGE Create a function that defines a CNN with Dropout
Use the create_model_intro() definition as the template,
create a new function called create_model_dropout()
Hint 1: Add one Dropout Layer that randomly drops 50 per cent of the input units.
Hint 2: Consider adding an additional layer(s) from one of the four layers we discussed.
OUTPUT
def create_model_dropout():
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_dropout = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_dropout = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_dropout)
# Pooling layer with input window sized 2x2
x_dropout = keras.layers.MaxPooling2D(pool_size=(2,2))(x_dropout)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_dropout = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_dropout)
# Second Pooling layer with input window sized 2x2
x_dropout = keras.layers.MaxPooling2D(pool_size=(2,2))(x_dropout)
# Third Convolutional layer with 64 filters, 3x3 kernel size, and ReLU activation
x_dropout = keras.layers.Conv2D(filters=64, kernel_size=(3,3), activation='relu')(x_dropout) # This is new!
# Dropout layer andomly drops 50 per cent of the input units
x_dropout = keras.layers.Dropout(rate=0.5)(x_dropout) # This is new!
# Flatten layer to convert 2D feature maps into a 1D vector
x_dropout = keras.layers.Flatten()(x_dropout)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_dropout = keras.layers.Dense(units=10, activation='softmax')(x_dropout)
# create the model
model_dropout = keras.Model(inputs = inputs_dropout,
outputs = outputs_dropout,
name = "cifar_model_dropout")
return model_dropoutCHALLENGE Does adding Dropout improve our model?
Create the dropout model.
Write the code to compile and fit our new dropout model using the same arguments we used for our model in the introduction.
Inspect the training metrics to determine whether the model has improved.
Save the dropout model.
Monitor the training progress.
PYTHON
# create the dropout model
model_dropout = create_model_dropout()
# compile the model
model_dropout.compile(optimizer = keras.optimizers.Adam(),
loss = keras.losses.CategoricalCrossentropy(),
metrics = keras.metrics.CategoricalAccuracy())
# fit the model
history_dropout = model_dropout.fit(x = train_images, y = train_labels,
batch_size = 32,
epochs = 10,
validation_data = (val_images, val_labels))
# save dropout model
model_dropout.save('fit_outputs/model_dropout.keras')
# inspect the training results
# convert the history to a dataframe for plotting
history_dropout_df = pd.DataFrame.from_dict(history_dropout.history)
# plot the loss and accuracy from the training process
fig, axes = plt.subplots(1, 2)
fig.suptitle('cifar_model_dropout')
sns.lineplot(ax=axes[0], data=history_dropout_df[['loss', 'val_loss']])
sns.lineplot(ax=axes[1], data=history_dropout_df[['categorical_accuracy', 'val_categorical_accuracy']])
val_loss_dropout, val_acc_dropout = model_dropout.evaluate(val_images, val_labels, verbose=2)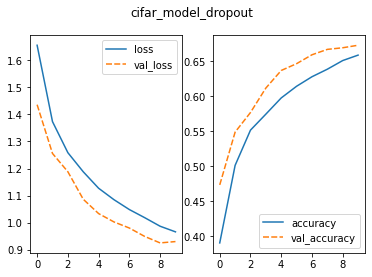
In this relatively uncommon situation, the training loss is higher than our validation loss while the validation accuracy is higher than the training accuracy. Using dropout, or other regularization techniques during training, can lead to a lower training accuracy.
Dropout randomly “drops out” units during training, which can prevent the model from fitting the training data too closely. This regularization effect may lead to a situation where the model generalizes better on the validation set.
The final accuracy on the validation set is higher than without dropout.
ChatGPT
Regularization methods introduce constraints or penalties to the training process, encouraging the model to be simpler and less prone to overfitting
Here are some common regularization methods for CNNs:
-
L1 and L2 Regularization are the two most common regularization techniques used in deep learning. They add a penalty term to the loss function during training to restrict the model’s weights.
- L1 regularization adds the absolute value of the weights to the loss function. It tends to produce sparse weight vectors, forcing some of the less important features to have exactly zero weights.
- L2 regularization adds the square of the weights to the loss function. It encourages the model to have smaller weights overall, preventing extreme values and reducing the impact of individual features.
- The regularization strength is controlled by a hyperparameter, often denoted as lambda (λ), that determines how much weight should be given to the regularization term. A larger λ value increases the impact of regularization, making the model simpler and more regularized.
Dropout: Involves randomly “dropping out” a fraction of neurons during training. This means during each training iteration, some neurons are temporarily removed from the network. Dropout effectively reduces the interdependence between neurons, preventing the network from relying too heavily on specific neurons, and making it more robust.
Batch Normalization: While not explicitly a regularization technique, Batch Normalization has a regularizing effect on the model. It normalizes the activations of each layer in the network, reducing internal covariate shift. This can improve training stability and reduce the need for aggressive dropout or weight decay.
Data Augmentation: Data augmentation is a technique where the training data is artificially augmented by applying various transformations like rotation, scaling, flipping, and cropping to create new examples. This increases the diversity of the training data and helps the model generalize better to unseen data.
Early Stopping: Early stopping is a form of regularization that stops the training process when the model’s performance on a validation set starts to degrade. It prevents the model from overfitting by avoiding further training after the point of best validation performance.
Using regularization techniques improves the generalization performance of CNNs and reduces the risk of overfitting. It’s essential to experiment with different regularization methods and hyperparameters to find the optimal combination for your specific CNN architecture and dataset.
Choose the best model and use it to predict
Based on our evaluation of the loss and accuracy metrics, we choose the model that appears to have the best performance of the models we have examined thus far. The next step is to use this model to predict the object classes on our test dataset.
- Use Model.compile() to compile a CNN.
- The choice of optimizer often depends on experimentation and empirical evaluation.
- The choice of loss function will depend on your data and aim.
- Use Model.fit() to make a train (fit) a CNN.
- Training/validation loss and accuracy can be used to evaluate a model during training.
- Dropout is one way regularization technique to prevent overfitting.
Content from Evaluate a Convolutional Neural Network and Make Predictions (Classifications)
Last updated on 2024-05-24 | Edit this page
Overview
Questions
- How do you use a model to make a prediction?
- How do you measure model prediction accuracy?
- What can you do to improve model performance?
- What is a hyperparameter?
Objectives
- Use a convolutional neural network (CNN) to make a prediction (i.e. classify an image).
- Explain how to measure the performance of a CNN.
- Know what steps to take to improve model accuracy.
- Explain hyperparameter tuning.
- Be familiar with advantages and disadvantages of different optimizers.
Step 7. Perform a Prediction/Classification
After you fully train the network to a satisfactory performance on the training and validation sets, we use it to perform predictions on a special hold-out set, the test set. The prediction accuracy of the model on new images will be used in Step 8. Measuring performance to measure the performance of the network.
Prepare test dataset
Recall in Episode 02 Introduction to
Image Data we discussed how to split your data into training and
test datasets and why. In most cases, that means you already have a test
set on hand. For example, we are using
keras.models.load_model to create a training and test
set.
When creating and using a test set there are a few things to check:
- It only contains images the model has never seen before.
- It is sufficiently large to provide a meaningful evaluation of model performance.
- It should include images from every target label plus images of classes not in your target set.
- It is processed in the same way as your training set.
Check to make sure you have a model in memory and a test dataset:
PYTHON
# load the CIFAR-10 dataset included with the keras library
(train_images, train_labels), (test_images, test_labels) = keras.datasets.cifar10.load_data()
# create a list of classnames
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
# normalize the RGB values to be between 0 and 1
test_images = test_images / 255.0
# check test image dataset is loaded - images and labels
print('Test: Images=%s, Labels=%s' % (test_images.shape, test_labels.shape))OUTPUT
Test: Images=(10000, 32, 32, 3), Labels=(10000, 1)CHALLENGE How big should our test data set be?
It depends! Recall in an Episode 02 Introduction to Image Data Callout we talked about the different ways to partition the data into training, validation and test data sets. For example, using the Stratified Sampling technique, we might split the data using these rations: 80-10-10 or 70-15-15.
The test set should be sufficiently large to provide a meaningful evaluation of your model’s performance. Smaller datasets might not provide a reliable estimate of how well your model generalizes.
Predict
Armed with a test dataset, we will choose our best performing CNN and use it to predict the class labels.
The Keras method to predict is found in the Model training APIs section of the documentation and has the following definition:
Model.predict(x, batch_size=None, verbose="auto", steps=None, callbacks=None)- x refers to the input samples which in our case is an array of images
CHALLENGE Write the code to make classname predictions on test data
Use the Model.predict function to predict the classnames
of your test data.
Hint 1: If not already in memory, use ‘keras.models.load_model()’
Hint 2: Capture the output of the predict method in a variable named ‘predictions’.
Question: What did the predict method return?
PYTHON
# load preferred model
model_best = keras.models.load_model('fit_outputs/model_dropout.keras')
print('We are using', model_best.name)
# use preferred model to predict
predictions = model_best.predict(x=test_images)
print(predictions)OUTPUT
We are using cifar_model_dropout
313/313 [==============================] - 1s 3ms/step
[[2.5438464e-03 2.8599051e-04 1.8983794e-02 ... 1.2449322e-03 2.1590138e-02 1.1813908e-03]
[1.4163133e-02 3.0712727e-01 6.2913182e-06 ... 7.1710346e-08 6.7631084e-01 2.3808377e-03]
[3.7576403e-02 3.7346989e-01 2.7308019e-04 ... 2.1147232e-04 4.7246802e-01 1.1511791e-01]
...
[3.6926474e-05 2.6195229e-07 4.9670707e-02 ... 5.6971662e-02 7.5488140e-05 1.2449813e-05]
[2.7443832e-02 3.4728521e-01 4.3887336e-02 ... 1.0875220e-01 1.4605661e-03 1.1823817e-02]
[6.4299519e-07 1.0424572e-05 6.5142207e-04 ... 9.7329682e-01 4.3226078e-07 5.3953562e-07]]Recall our model will return a vector of probabilities, one for each class. By finding the class with the highest probability, we can select the most likely class name of the object. We will use numpy.argmax() to find the class with the highest probability in each row.
PYTHON
# convert probability predictions to table using class names for column names
prediction_df = pd.DataFrame(data=predictions, columns=class_names)
# inspect
print(prediction_df.head())
# convert predictions to class labels
predicted_labels = np.argmax(a=predictions, axis=1)
print(predicted_labels)OUTPUT
We are using cifar_model_dropout
airplane automobile bird ... horse ship truck
0 0.165748 -0.118394 0.062156 ... 0.215477 0.013811 -0.047446
1 0.213530 -0.126139 0.052813 ... 0.264517 0.009097 -0.091710
2 0.211900 -0.099055 0.047890 ... 0.242345 -0.014492 -0.073153
3 0.187883 -0.085144 0.044609 ... 0.217864 0.007502 -0.055209
4 0.190110 -0.118892 0.054869 ... 0.252434 -0.030064 -0.061485
[5 rows x 10 columns]
Out [5]: array([3, 8, 8, ..., 5, 1, 7], dtype=int64)Step 8. Measuring performance
After using our preferred model to make predictions on a test dataset of unseen images we want to know how well it performed. There are many different methods available for measuring performance and which one to use depends on the type of task we are attempting.
A quick and easy way to check the accuracy of our model is to use the
accuracy_score() from sklearn.metrics. This
function takes as a first parameter the true labels of the test set. The
second parameter is the predicted labels from our model.
PYTHON
from sklearn.metrics import accuracy_score
# evaluate the model on the test data set
test_acc = accuracy_score(y_true=test_labels, y_pred=predicted_labels)
print('Accuracy:', round(test_acc,2))OUTPUT
Accuracy: 0.67To understand a bit more about how this accuracy is obtained, we can create a confusion matrix.
Confusion matrix
In the case of multiclass classifications, each cell value (Ci,j) is equal to the number of observations known to be in group i and predicted to be in group j. The diagonal cells in the matrix are where the true class and predicted class match.
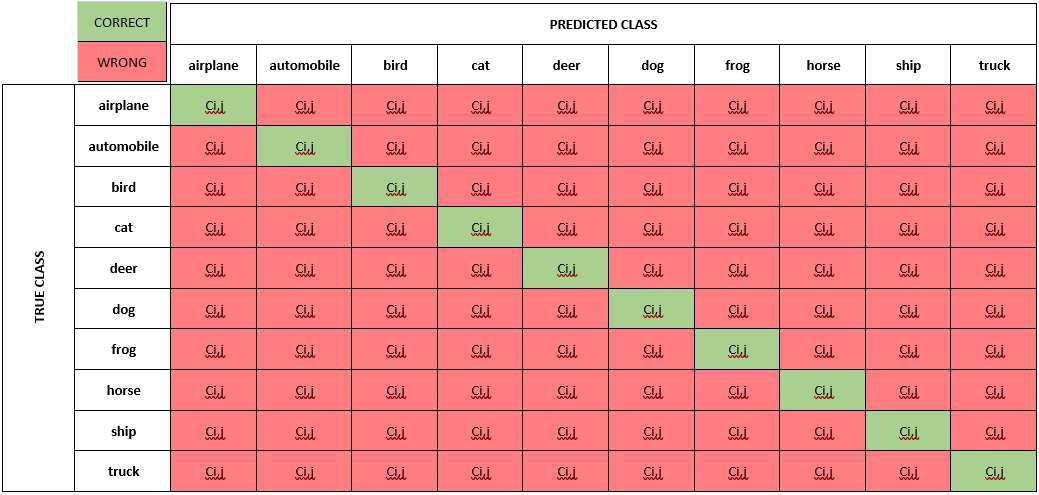
To create a confusion matrix in python, we use another convenient
function from sklearn.metrics called
confusion_matrix. This function takes the same two
parameters we just used, the true labels and the predicted labels.
PYTHON
from sklearn.metrics import confusion_matrix
# create a confusion matrix
conf_matrix = confusion_matrix(y_true=test_labels, y_pred=predicted_labels)
print(conf_matrix)OUTPUT
[[682 36 67 13 15 7 27 11 108 34]
[ 12 837 3 2 6 3 32 0 29 76]
[ 56 4 462 37 137 72 184 26 13 9]
[ 10 13 48 341 87 217 221 27 17 19]
[ 23 4 38 34 631 23 168 63 13 3]
[ 8 9 59 127 74 550 103 51 10 9]
[ 3 3 18 23 18 12 919 2 1 1]
[ 14 8 24 28 98 75 34 693 2 24]
[ 56 39 11 17 4 6 22 2 813 30]
[ 23 118 6 12 6 5 33 15 35 747]]Unfortunately, this matrix is hard to read. It’s not clear which column and which row correspond to which class. We can convert the matrix to a pandas dataframe using the class labels for its index (rows) and columns.
PYTHON
# Convert confustion matrix to a pandas dataframe
confusion_df = pd.DataFrame(data=conf_matrix, index=class_names, columns=class_names)
# Set the names of the x and y axis, this helps with the readability of the heatmap
confusion_df.index.name = 'True Label'
confusion_df.columns.name = 'Predicted Label'We can then use the heatmap function from seaborn to create a nice
visualization of the confusion matrix.
- The
annot=Trueparameter here will put the numbers from the confusion matrix in the heatmap. - The
fmt=3gwill display the values with three significant digits.
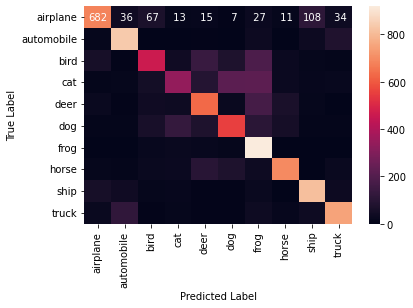
CHALLENGE Confusion Matrix
Measure the performance of the neural network you trained and visualized as a confusion matrix.
Q1. Did the neural network perform well on the test set?
Q2. Did you expect this from the training loss plot?
Q3. What could we do to improve the performance?
A1. The confusion matrix illustrates that the predictions are not bad but can be improved.
A2. I expected the performance to be better than average because the accuracy of the model I chose was 67 per cent on the validation set.
A3. We can try many things to improve the performance from here. One of the first things we can try is to change the network architecture. However, in the interest of time, and given we already learned how to build a CNN, we will now change the training parameters.
Step 9. Tune hyperparameters
Recall the following from Episode 01 Introduction to Deep Learning:
What are hyperparameters?
Hyperparameters are the parameters set by the person configuring the model instead of those learned by the algorithm itself. Like the dials on a radio which are tuned to the best frequency, hyperparameters can be tuned to the best combination for a given model and context.
These hyperparameters can include the learning rate, the number of layers in the network, the number of neurons per layer, and many more. The tuning process is systematic searching for the best combination of hyperparameters to optimize the model’s performance.
In some cases, it might be necessary to adjust these and re-run the training many times before we are happy with the result.
Table 1. List of some of the hyperparameters to tune and when.
| During Build | When Compiling | During Training |
|---|---|---|
| number of neurons | loss function | epoch |
| activation function | optimizer | batch size |
| dropout rate | learning rate |
There are a number of techniques used to tune hyperparameters. Let us explore a few of them.
One common method for hyperparameter tuning is by using a
for loop to change a particular parameter.
CHALLENGE Tune Dropout Rate (Model Build) using a For Loop
Q1. What do you think would happen if you lower the dropout rate? Write some code to vary the dropout rate and investigate how it affects the model training.
SH
Hint 1: Modify the 'create_model_dropout()' function and define a `create_model_dropout_vary` function that has `dropout_rate` as its only parameter.
Hint 2: Use a for loop to call your function with varying dropout ratesQ2. You are varying the dropout rate and checking its effect on the model performance, what is the term associated to this procedure?
A1. Varying the dropout rate
The code below instantiates and trains a model with varying dropout rates. The resulting plot indicates the ideal dropout rate in this case is around 0.45. This is where the validation loss is lowest.
SH
NB1: It takes a while to train these five networks.
NB2: You should do this with a test set and not with the validation set!PYTHON
# define new dropout function that accepts a dropout rate
def create_model_dropout_vary(dropout_rate):
# Input layer of 32x32 images with three channels (RGB)
inputs_vary = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_vary = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_vary)
# Pooling layer with input window sized 2x2
x_vary = keras.layers.MaxPooling2D(pool_size=(2,2))(x_vary)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_vary = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_vary)
# Second Pooling layer with input window sized 2x2
x_vary = keras.layers.MaxPooling2D(pool_size=(2,2))(x_vary)
# Second Convolutional layer with 64 filters, 3x3 kernel size, and ReLU activation
x_vary = keras.layers.Conv2D(filters=64, kernel_size=(3,3), activation='relu')(x_vary)
# Dropout layer randomly drops x% of the input units
x_vary = keras.layers.Dropout(rate=dropout_rate)(x_vary) # This is new!
# Flatten layer to convert 2D feature maps into a 1D vector
x_vary = keras.layers.Flatten()(x_vary)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_vary = keras.layers.Dense(units=10, activation='softmax')(x_vary)
model_vary = keras.Model(inputs = inputs_vary,
outputs = outputs_vary,
name ="cifar_model_dropout_vary")
return model_vary
# specify range of dropout rates
dropout_rates = [0.15, 0.3, 0.45, 0.6, 0.75]
# create empty list to hold losses
val_losses_vary = []
# use for loop to explore varying the dropout rate
for dropout_rate in dropout_rates:
# create the model
model_vary = create_model_dropout_vary(dropout_rate)
# compile the model
model_vary.compile(optimizer = keras.optimizers.Adam(),
loss = keras.losses.CategoricalCrossentropy(),
metrics = keras.metrics.CategoricalAccuracy())
# fit the model
model_vary.fit(x = train_images, y = train_labels,
batch_size = 32,
epochs = 10,
validation_data = (val_images, val_labels)))
# evaluate the model on the test data set
val_loss_vary, val_acc_vary = model_vary.evaluate(val_images, val_labels)
# save the evaulation metrics
val_losses_vary.append(val_loss_vary)
# convert rates and metrics to dataframe for plotting
loss_df = pd.DataFrame({'dropout_rate': dropout_rates, 'val_loss_vary': val_losses_vary})
# plot the loss and accuracy from the training process
sns.lineplot(data=loss_df, x='dropout_rate', y='val_loss_vary')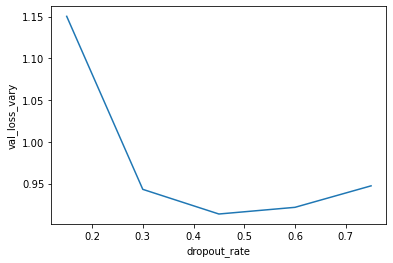
A2. Term associated to this procedure
Another common method for hyperparameter tuning is grid search.
What is Grid Search?
Grid Search or GridSearchCV (as per the library function
call) is foundation method for hyperparameter tuning. The aim of
hyperparameter tuning is to define a grid of possible values for each
hyperparameter you want to tune. GridSearch will then evaluate the model
performance for each combination of hyperparameters in a brute-force
manner, iterating through every possible combination in the grid.
For instance, suppose you’re tuning two hyperparameters:
Learning rate: with possible values [0.01, 0.1, 1]
Batch size: with possible values [10, 50, 100]
GridSearch will evaluate the model for all 3*3 = 9 combinations (e.g., {0.01, 10}, {0.01, 50}, {0.1, 10}, and so on).
CHALLENGE Tune Optimizer using Grid Search
In Episode 04 Compile and Train a
Convolutional Neural Network we talked briefly about the
Adam optimizer used in our Model.compile
discussion. Recall the optimizer refers to the
algorithm with which the model learns to optimize on the provided loss
function.
Write some code to demonstrate how GridSearch works.
Hint 1: Use the create_model_intro() definition as the
build function to use during GridSearch and modify it
to include the ‘Model.compile’ method call.
PYTHON
# use the intro model for gridsearch and add compile method call
def create_model_intro():
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)
# create the model
model_intro = keras.Model(inputs = inputs_intro,
outputs = outputs_intro,
name = "cifar_model_intro")
# compile the model
model_intro.compile(optimizer = keras.optimizers.Adam(),
loss = keras.losses.CategoricalCrossentropy(),
metrics = keras.metrics.CategoricalAccuracy())
return model_introSecondly, we can define our GridSearch parameters and assign fit results to a variable for output.
PYTHON
from scikeras.wrappers import KerasClassifier
from sklearn.model_selection import GridSearchCV
# Instantiate wrapper class for GridSearchCV
model = KerasClassifier(build_fn=create_model_intro, epochs=2, batch_size=32, verbose=0) # epochs, batch_size, verbose can be adjusted as required. Using low epochs to save computation time and demonstration purposes only
# Define the grid search parameters
optimizer = ['SGD', 'RMSprop', 'Adam']
param_grid = dict(optimizer=optimizer)
# search over specified parameter values for an estimator
grid = GridSearchCV(estimator=model, param_grid=param_grid, n_jobs=1, cv=3)
# run fit with all parameters
grid_result = grid.fit(train_images, train_labels)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))OUTPUT
Best: 0.586660 using {'optimizer': 'RMSprop'}Thus, we can interpret from this output that our best tested optimiser is the root mean square propagation optimiser, or RMSprop.
Curious about RMSprop? RMSprop in Keras and RMSProp, Cornell University
Here is a third example of tuning hyperparameters, this time using a for loop to tune the activation function.
Activation Functions
In Episode 03 Build a Convolutional
Neural Network we talked briefly about the relu
activation function passed as an argument to our Conv2D
hidden layers.
An activation function is like a switch, or a filter, that we use in artificial neural networks, inspired by how our brains work. These functions play a crucial role in determining whether a neuron (a small unit in the neural network) should “fire” or become active.
Think of an activation function as a tiny decision-maker for each neuron in a neural network. It helps determine whether the neuron should ‘fire’, or pass on information, or stay ‘off’ and remain silent, much like a light switch controls whether the light should be ON or OFF. Activation functions are crucial because they add non-linearity to the neural network. Without them, the network would be like a simple linear model, unable to learn complex patterns in data.
How do you know what activation function to choose?
Neural networks can be tuned to leverage many different types of activation functions. In fact, it is a crucial decision as the choice of activation function will have a direct impact on the performance of the model.
Table 2. Description of each activation function, its benefits, and drawbacks.
| Activation Function | Positives | Negatives |
|---|---|---|
| ReLU | - Addresses vanishing gradient problem - Computationally efficient |
- Can cause “dying neurons” - Not zero-centered |
| Leaky ReLU | - Addresses the “dying ReLU” problem - Computationally efficient |
- Empirical results can be inconsistent - Not zero-centered |
| Sigmoid | - Outputs between 0 and 1 - Smooth gradient |
- Can cause vanishing gradient problem - Computationally more expensive |
| Tanh | - Outputs between -1 and 1 - Zero-centered |
- Can still suffer from vanishing gradients to some extent |
| Softmax | - Used for multi-class classification - Outputs a probability distribution |
- Used only in the output layer for classification tasks |
| SELU | - Self-normalizing properties - Can outperform ReLU in deeper networks |
- Requires specific weight initialization - May not perform well outside of deep architectures |
CHALLENGE Tune Activation Function using For Loop
Write some code to assess activation function performance.
Hint 1: Use the create_model_intro() definition as the
build function to use during GridSearch. Make
modifications to take a single parameter ‘activation_function and this
time include the ’Model.compile’ method call in the definition.
The code below serves as a practical means for exploring activation performance on an image dataset.
PYTHON
# modify the intro model to sample activation functions
def create_model_act(activation_function):
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_act = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_act = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation=activation_function)(inputs_act)
# Pooling layer with input window sized 2x2
x_act = keras.layers.MaxPooling2D((2, 2))(x_act)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_act = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation=activation_function)(x_act)
# Second Pooling layer with input window sized 2x2
x_act = keras.layers.MaxPooling2D(pool_size=(2,2))(x_act)
# Flatten layer to convert 2D feature maps into a 1D vector
x_act = keras.layers.Flatten()(x_act)
# Dense layer with 64 neurons and ReLU activation
x_act = keras.layers.Dense(units=64, activation=activation_function)(x_act)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_act = keras.layers.Dense(units=10, activation='softmax')(x_act)
# create the model
model_act = keras.Model(inputs = inputs_act,
outputs = outputs_act,
name="cifar_model_activation")
# compile the model
model_act.compile(optimizer = keras.optimizers.Adam(),
loss = keras.losses.CategoricalCrossentropy(),
metrics = keras.metrics.CategoricalAccuracy())
return model_act
# create a ist of activation functions to try
activations = ['relu', 'sigmoid', 'tanh', 'selu', keras.layers.LeakyReLU()]
# create a dictionary object to store the training history
history_data = {}
# train the model with each activation function and store the history
for activation in activations:
model = create_model(activation)
history = model.fit(x = train_images, y = train_labels,
batch_size = 32,
epochs = 10,
validation_data = (val_images, val_labels))
# plot the validation accuracy for each activation function
plt.figure(figsize=(12, 6))
for activation, history in history_data.items():
plt.plot(history.history['val_categorical_accuracy'], label=activation)
plt.title('Validation accuracy for different activation functions')
plt.xlabel('Epochs')
plt.ylabel('Validation Accuracy')
plt.legend()
plt.show()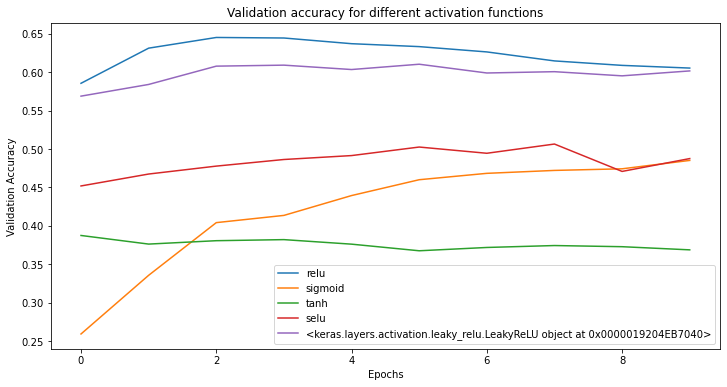
In this figure, after 10 epochs, the ReLU and
Leaky ReLU activation functions appear to converge around
0.60 per cent validation accuracy. We recommend when tuning your model
to ensure you use enough epochs to be confident in your results.
CHALLENGE What could be next steps to further improve the model?
With unlimited options to modify the model architecture or to play with the training parameters, deep learning can trigger very extensive hunting for better and better results. Usually models are “well behaving” in the sense that small chances to the architectures also only result in small changes of the performance (if any). It is often tempting to hunt for some magical settings that will lead to much better results. But do those settings exist? Applying common sense is often a good first step to make a guess of how much better could results be.
- What changes to the model architecture might make sense to explore?
- Ignoring changes to the model architecture, what might notably improve the prediction quality?
This is an open question.
Regarding the model architecture:
- In the present case we do not see a magical silver bullet to suddenly boost the performance. But it might be worth testing if deeper networks do better (more layers).
Other changes that might impact the quality notably:
- The most obvious answer here would be: more data! Even this will not always work (e.g., if data is very noisy and uncorrelated, more data might not add much).
- Related to more data: use data augmentation. By creating realistic variations of the available data, the model might improve as well.
- More data can mean more data points and also more features!
By now you should have a well-trained, finely-tuned model that makes accurate predictions and are ready to share the model with others.
- Model accuracy must be measured on a test dataset with images your model has not seen before.
- Use Model.predict() to make a prediction with your model.
- There are many hyperparameters to choose from to improve model performance.
- Fitting separate models with different hyperparameters and comparing their performance is a common and good practice in deep learning.
