Build a Convolutional Neural Network
Last updated on 2024-05-30 | Edit this page
Overview
Questions
- What is a (artificial) neural network (ANN)?
- How is a convolutional neural network (CNN) different from an ANN?
- What are the types of layers used to build a CNN?
Objectives
- Understand how a convolutional neural network (CNN) differs from an artificial neural network (ANN).
- Explain the terms: kernel, filter.
- Know the different layers: convolutional, pooling, flatten, dense.
Neural Networks
A neural network is an artificial intelligence technique loosely based on the way neurons in the brain work.
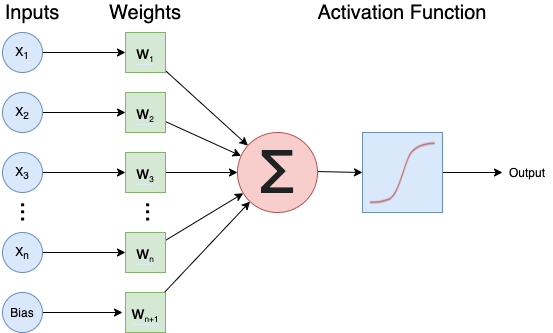
A single neuron
Each neuron will:
- Take one or more inputs (\(x_1, x_2, ...\)), e.g., floating point numbers, each with a corresponding weight.
- Calculate the weighted sum of the inputs where ($w_1, w_2, … $) indicate weights.
- Add an extra constant weight (i.e. a bias term) to this weighted sum.
- Apply a non-linear function to the bias-adjusted weighted sum.
- Return one output value, again a floating point number.
One example equation to calculate the output for a neuron is:
\(output=ReLU(∑i(xi∗wi)+bias)\)
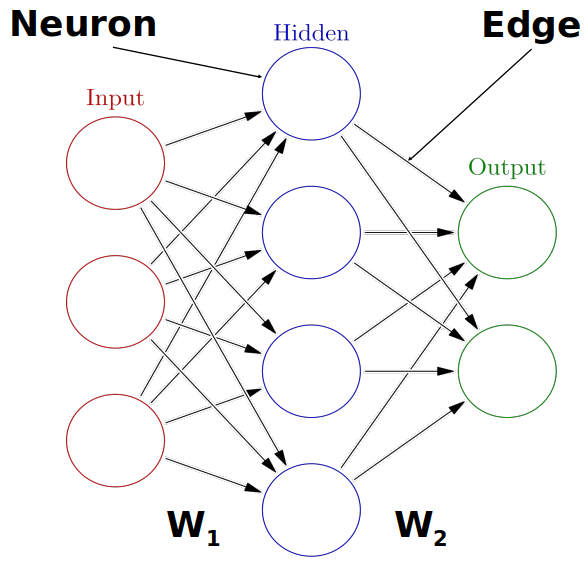
Combining multiple neurons into a network
Multiple neurons can be joined together by connecting the output of one to the input of another. These connections are also associated with weights that determine the ‘strength’ of the connection, and these weights are also adjusted during training. In this way, the combination of neurons and connections describe a computational graph, an example can be seen in the image below.
In most neural networks neurons are aggregated into layers. Signals travel from the input layer to the output layer, possibly through one or more intermediate layers called hidden layers. The image below illustrates an example of a neural network with three layers, each circle is a neuron, each line is an edge and the arrows indicate the direction data moves in.
Neural networks aren’t a new technique, they have been around since the late 1940s. But until around 2010 neural networks tended to be quite small, consisting of only 10s or perhaps 100s of neurons. This limited them to only solving quite basic problems. Around 2010 improvements in computing power and the algorithms for training the networks made much larger and more powerful networks practical. These are known as deep neural networks or Deep Learning.
Convolutional Neural Networks
A convolutional neural network (CNN) is a type of artificial neural network (ANN) most commonly applied to analyze visual imagery. They are specifically designed for processing grid-like data, such as images, by leveraging convolutional layers that preserve spatial relationships, when extracting features.
Step 4. Build an architecture from scratch or choose a pretrained model
Let us explore how to build a neural network from scratch. Although this sounds like a daunting task, with Keras it is surprisingly straightforward. With Keras you compose a neural network by creating layers and linking them together.
Parts of a neural network
There are three main components of a neural network:
- CNN Part 1. Input Layer
- CNN Part 2. Hidden Layers
- CNN Part 3. Output Layer
The output from each layer becomes the input to the next layer.
CNN Part 1. Input Layer
The Input in Keras gets special treatment when images are used. Keras
automatically calculates the number of inputs and outputs a specific
layer needs and therefore how many edges need to be created. This means
we just need to let Keras know how big our input is going to be. We do
this by instantiating a keras.Input class and passing it a
tuple to indicate the dimensionality of the input data. In Python, a
tuple is a data type used to store collections of data.
It is similar to a list, but tuples are immutable, meaning once they are
created, their contents cannot be changed.
The input layer is created with the keras.Input function
and its first parameter is the expected shape of the input:
keras.Input(shape=None, batch_size=None, dtype=None, sparse=None, batch_shape=None, name=None, tensor=None)In our case, the shape of an image is defined by its pixel dimensions and number of channels:
OUTPUT
(40000, 32, 32, 3) # number of images, image width in pixels, image height in pixels, number of channels (RGB)CHALLENGE Create the input layer for our network
Hint 1: Specify shape argument only and use defaults for the rest.
Hint 2: The shape of our input dataset includes the total number of images. We want to take a slice of the shape for a single individual image to use an input.
OUTPUT
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])CNN Part 2. Hidden Layers
The next component consists of the so-called hidden layers of the network.
In a neural network, the input layer receives the raw data, and the output layer produces the final predictions or classifications. These layers’ contents are directly observable because you can see the input data and the network’s output predictions.
However, the hidden layers, which lie between the input and output layers, contain intermediate representations of the input data. These representations are transformed through various mathematical operations performed by the network’s neurons. The specific values and operations within these hidden layers are not directly accessible or interpretable from the input or output data. Therefore, they are considered “hidden” from external observation or inspection.
In a CNN, the hidden layers typically consist of convolutional, pooling, reshaping (e.g., Flatten), and dense layers.
Check out the Layers API section of the Keras documentation for each layer type and its parameters.
Convolutional Layers
A convolutional layer is a fundamental building block in a CNN designed for processing structured, gridded data, such as images. It applies convolution operations to input data using learnable filters or kernels, extracting local patterns and features (e.g. edges, corners). These filters enable the network to capture hierarchical representations of visual information, allowing for effective feature learning.
To find the particular features of an image, CNNs make use of a concept from image processing that precedes Deep Learning.
A convolution matrix, or kernel, is a matrix transformation that we ‘slide’ over the image to calculate features at each position of the image. For each pixel, we calculate the matrix product between the kernel and the pixel with its surroundings. Here is one example of a 3x3 kernel used to detect edges:
[[-1, -1, -1],
[0, 0, 0]
[1, 1, 1]]This kernel will give a high value to a pixel if it is on a horizontal border between dark and light areas.
In the following image, the effect of such a kernel on the values of a single-channel image stands out. The red cell in the output matrix is the result of multiplying and summing the values of the red square in the input, and the kernel. Applying this kernel to a real image demonstrates it does indeed detect horizontal edges.
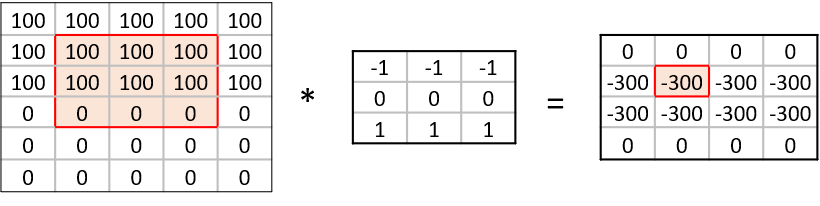
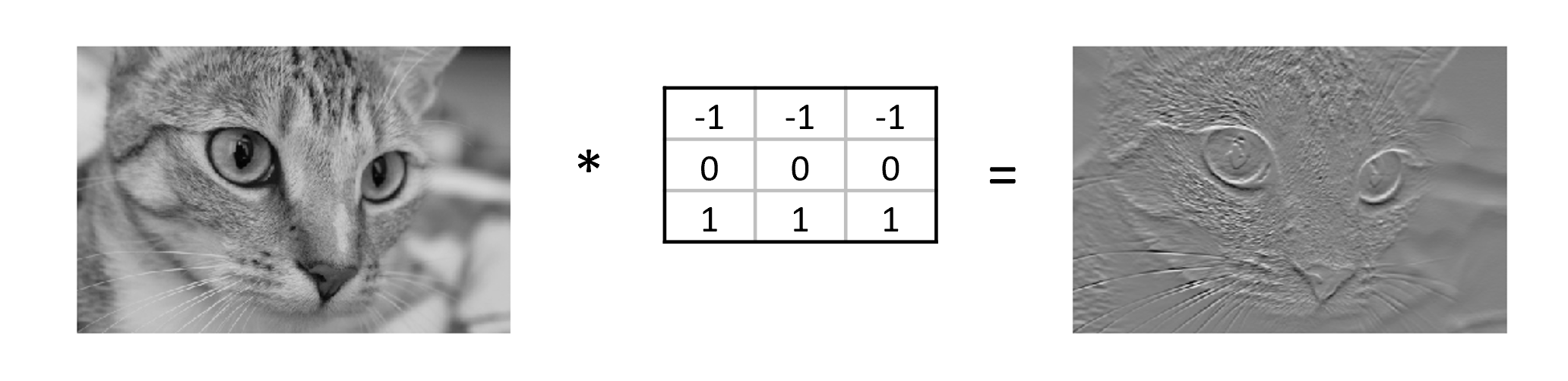
There are several types of convolutional layers available in Keras depending on your application. We use the two-dimensional layer typically used for images:
keras.layers.Conv2D(filters, kernel_size, strides=(1, 1), padding="valid", activation=None, **kwargs)-
filtersis the number of filters in this layer.- This is one of the hyperparameters of our system and should be chosen carefully.
- Good practice is to start with a relatively small number of filters in the first layer to prevent overfitting.
- Choosing a number of filters as a power of two (e.g., 32, 64, 128) is common.
-
kernel sizeis the size of the convolution matrix which we already discussed. - Smaller kernels are often used to capture fine-grained features and odd-sized filters are preferred because they have a centre pixel which helps maintain spatial symmetry during convolutions. -
activationspecifies which activation function to use.
When specifying layers, remember each layer’s output is the input to the next layer. We must create a variable to store a reference to the output so we can pass it to the next layer. The basic format for doing this is:
output_variable = layer_name(layer_arguments)(input_variable)
CHALLENGE Create a 2D convolutional layer for our network
Create a Conv2D layer with 16 filters, a 3x3 kernel size, and the ‘relu’ activation function.
Here we choose relu which is one of the most
commonly used in deep neural networks that is proven to work well. We
will discuss activation functions later in Step 9. Tune
hyperparameters but to satisfy your curiosity,
ReLU stands for Rectified Linear Unit (ReLU).
Hint 1: The input to each layer is the output of the previous layer.
OUTPUT
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)Playing with convolutions
Convolutions applied to images can be hard to grasp at first. Fortunately, there are resources out there that enable users to interactively play around with images and convolutions:
Image kernels explained illustrates how different convolutions can achieve certain effects on an image, like sharpening and blurring.
The convolutional neural network cheat sheet provides animated examples of the different components of convolutional neural nets.
Pooling Layers
The convolutional layers are often intertwined with Pooling layers. As opposed to the convolutional layer used in feature extraction, the pooling layer alters the dimensions of the image and reduces it by a scaling factor effectively decreasing the resolution of your picture.
The rationale behind this is that higher layers of the network should focus on higher-level features of the image. By introducing a pooling layer, the subsequent convolutional layer has a broader ‘view’ on the original image.
Similar to convolutional layers, Keras offers several pooling layers and one used for images (2D spatial data):
keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, padding="valid", data_format=None, name=None, **kwargs)-
pool_size, i.e., the size of the pooling window- In Keras, the default is usually (2, 2)
The function downsamples the input along its spatial dimensions (height and width) by taking the maximum value over an input window (of size defined by pool_size) for each channel of the input. By taking the maximum instead of the average, the most prominent features in the window are emphasized.
For example, a 2x2 pooling size reduces the width and height of the input by a factor of 2. Empirically, a 2x2 pooling size has been found to work well in various for image classification tasks and also strikes a balance between down-sampling for computational efficiency and retaining important spatial information.
OUTPUT
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)Dense layers
A dense layer is a fully connected layer where each neuron receives input from every neuron in the previous layer. When connecting the layer to its input and output layers every neuron in the dense layer gets an edge (i.e. connection) to all of the input neurons and all of the output neurons.
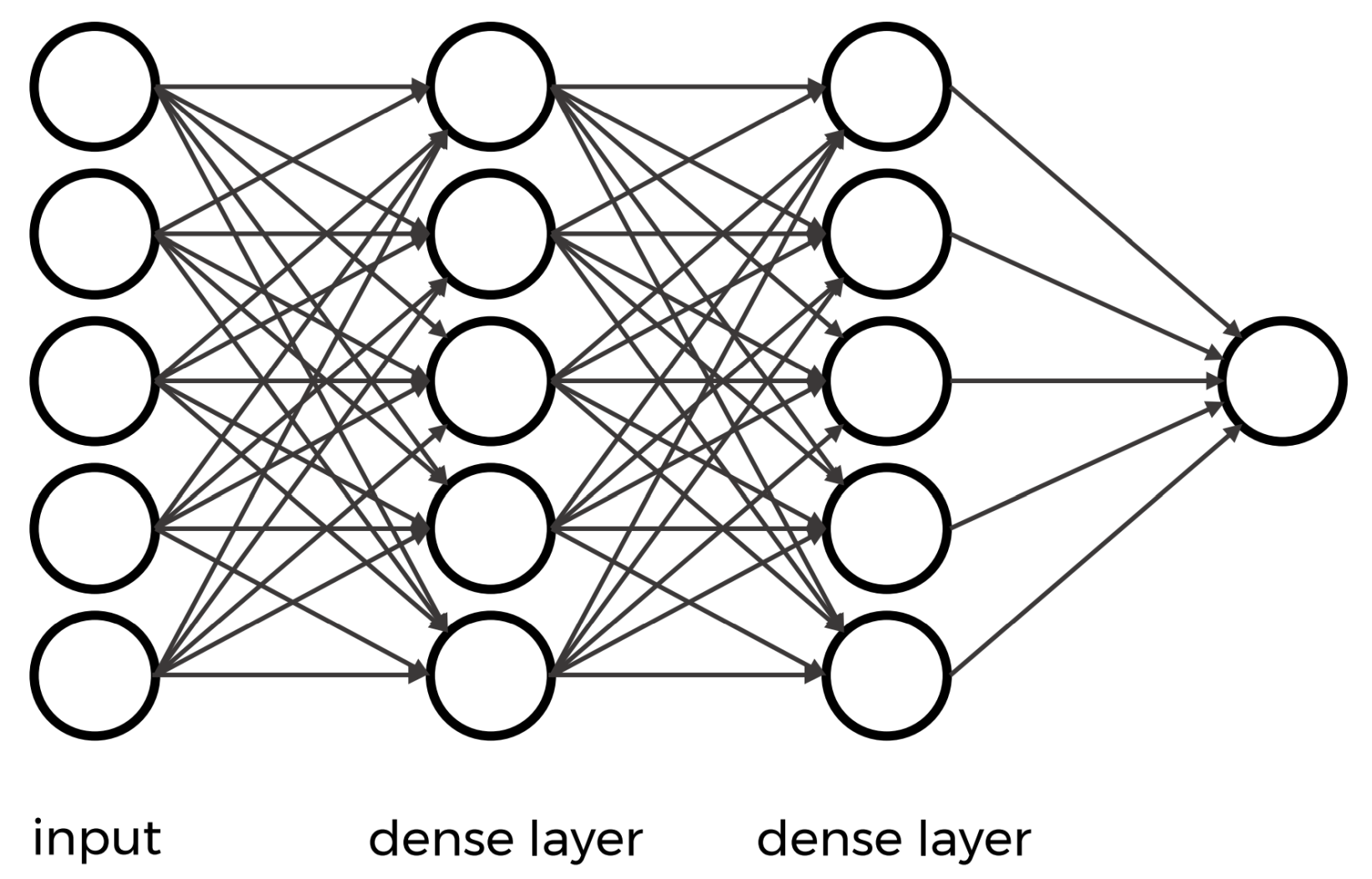
This layer aggregates global information about the features learned in previous layers to make a decision about the class of the input.
In Keras, a densely-connected layer is defined:
keras.layers.Dense(units, activation=None, **kwargs)- `units in this case refers to the number of neurons.
The choice of how many neurons to specify is often determined through experimentation and can impact the performance of our CNN. Too few neurons may not capture complex patterns in the data but too many neurons may lead to overfitting.
OUTPUT
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)Reshaping Layers: Flatten
The next type of hidden layer used in our introductory model is a
type of reshaping layer defined in Keras by the
keras.layers.Flatten class. It is necessary when
transitioning from convolutional and pooling layers to fully connected
layers.
keras.layers.Flatten(data_format=None, **kwargs)The Flatten layer converts the output of the previous layer into a single one-dimensional vector that can be used as input for a dense layer.
OUTPUT
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)A flatten layer function is typically used to transform the two-dimensional arrays (matrices) generated by the convolutional and pooling layers into a one-dimensional array. This is necessary when transitioning from the convolutional/pooling layers to the fully connected layers, which require one-dimensional input.
During the convolutional and pooling operations, a neural network extracts features from the input images, resulting in multiple feature maps, each represented by a matrix. These feature maps capture different aspects of the input image, such as edges, textures, or patterns. However, to feed these features into a fully connected layer for classification or regression tasks, they must be a single vector.
The flatten layer takes each element from the feature maps and arranges them into a single long vector, concatenating them along a single dimension. This transformation preserves the spatial relationships between the features in the original image while providing a suitable format for the fully connected layers to process.
Is one layer of each type enough?
Not for complex data!
A typical architecture for image classification is likely to include at least one convolutional layer, one pooling layer, one or more dense layers, and possibly a flatten layer.
Convolutional and Pooling layers are often used together in multiple sets to capture a wider range of features and learn more complex representations of the input data. Using this technique, the network can learn a hierarchical representation of features, where simple features detected in early layers are combined to form more complex features in deeper layers.
There isn’t a strict rule of thumb for the number of sets of convolutional and pooling layers to start with, however, there are some guidelines.
We are starting with a relatively small and simple architecture because we are limited in time and computational resources. A simple CNN with one or two sets of convolutional and pooling layers can still achieve decent results for many tasks but for your network you will experiment with different architectures.
OUTPUT
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)CNN Part 3. Output Layer
Recall for the outputs we asked ourselves what we want to identify from the data. If we are performing a classification problem, then typically we have one output for each potential class.
In traditional CNN architectures, a dense layer is typically used as the final layer for classification. This dense layer receives the flattened feature maps from the preceding convolutional and pooling layers and outputs the final class probabilities or regression values.
For multiclass data, the softmax activation is used
instead of relu because it helps the computer give each
option (class) a likelihood score, and the scores add up to 100 per
cent. This way, it’s easier to pick the one the computer thinks is most
probable.
CHALLENGE Create an Output layer for our network
Use a dense layer to create the output layer for a classification problem with 10 possible classes.
Hint 1: The input to each layer is the output of the previous layer.
Hint 2: The units (neurons) should be the same as number of classes as our dataset.
Hint 3: Use softmax activation.
OUTPUT
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)Putting it all together
Once you decide on the initial architecture of your CNN, the last
step to create the model is to bring all of the parts together using the
keras.Model class.
There are several ways of grouping the layers into an object as described in the Keras Models API.
We will use the Functional API to create our model using the inputs and outputs defined in this episode.
keras.Model(inputs=inputs, outputs=outputs)Note that there is additional argument that can be passed to the keras.Model class called ‘name’ that takes a string. Although it is no longer specified in the documentation, the ‘name’ argument is useful when deciding among different architectures.
CHALLENGE Create a function that defines an introductory CNN
Using the keras.Model class and the input, hidden, and output layers from the previous challenges, create a function that returns the CNN from the introduction.
Hint 1: Name the model “cifar_model_intro”
OUTPUT
def create_model_intro():
# CNN Part 1
# Input layer of 32x32 images with three channels (RGB)
inputs_intro = keras.Input(shape=train_images.shape[1:])
# CNN Part 2
# Convolutional layer with 16 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=16, kernel_size=(3,3), activation='relu')(inputs_intro)
# Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Second Convolutional layer with 32 filters, 3x3 kernel size, and ReLU activation
x_intro = keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation='relu')(x_intro)
# Second Pooling layer with input window sized 2x2
x_intro = keras.layers.MaxPooling2D(pool_size=(2,2))(x_intro)
# Flatten layer to convert 2D feature maps into a 1D vector
x_intro = keras.layers.Flatten()(x_intro)
# Dense layer with 64 neurons and ReLU activation
x_intro = keras.layers.Dense(units=64, activation='relu')(x_intro)
# CNN Part 3
# Output layer with 10 units (one for each class) and softmax activation
outputs_intro = keras.layers.Dense(units=10, activation='softmax')(x_intro)
# create the model
model_intro = keras.Model(inputs = inputs_intro,
outputs = outputs_intro,
name = "cifar_model_intro")
return model_introWe now have a function that defines the introduction model.
We can use this function to create the introduction model and and
view a summary of its structure using the Model.summary
method.
PYTHON
# create the introduction model
model_intro = create_model_intro()
# view model summary
model_intro.summary()OUTPUT
Model: "cifar_model_intro"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
conv2d (Conv2D) (None, 30, 30, 16) 448
max_pooling2d (MaxPooling2 (None, 15, 15, 16) 0
D)
conv2d_1 (Conv2D) (None, 13, 13, 32) 4640
max_pooling2d_1 (MaxPoolin (None, 6, 6, 32) 0
g2D)
flatten (Flatten) (None, 1152) 0
dense (Dense) (None, 64) 73792
dense_1 (Dense) (None, 10) 650
=================================================================
Total params: 79530 (310.66 KB)
Trainable params: 79530 (310.66 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________The Model.summary() output has three columns:
- Layer (type) lists the name and type of each layer.
- Remember the ‘name’ argument we used to name our model? This argument can also be supplied to each layer. If a name is not provided, Keras will assign a unique identifier starting from 1 and incrementing for each new layer of the same type within the model.
- Output Shape describes the shape of the output produced by each
layer as (batch_size, height, width, channels).
- Batch size is the number of samples processed in each batch during training or inference. This dimension is often denoted as None in the summary because the batch size can vary and is typically specified during model training or inference.
- Height, Width, Channels: The remaining dimensions represent the spatial dimensions and the number of channels in the output tensor. For convolutional layers and pooling layers, the height and width dimensions typically decrease as the network progresses through the layers due to the spatial reduction caused by convolution and pooling operations. The number of channels may change depending on the number of filters in the convolutional layer or the design of the network architecture.
- For example, in a convolutional layer, the output shape (None, 30,
30, 16) means:
- None: The batch size can vary.
- 30: The height and width of the output feature maps are both 30 pixels.
- 16: There are 16 channels in the output feature maps, indicating that the layer has 16 filters.
- Param # displays the number of parameters (weights and biases)
associated with each layer.
- The total number of parameters in a layer is calculated as follows:
- Total parameters = (number of input units) × (number of output units) + (number of output units)
- At the bottom of the Model.summary() you will find the number of
Total parameters and their size; the number of Trainable parameters and
their size; and the number of Non-trainable parameters and their size.
- In most cases, the total number of parameters will match the number of trainable parameters. In other cases, such as models using normalization layers, there will be some parameters that are fixed during training and not trainable.
- Disclaimer: We explicitly decided to focus on building a foundational understanding of convolutional neural networks for this course without delving into the detailed calculation of parameters. However, as your progress on your deep learning journey it will become increasingly important for you to understand parameter calculation in order to optimize model performance, troubleshoot issues, and design more efficient CNN architectures.
- The total number of parameters in a layer is calculated as follows:
How to choose an architecture?
For this neural network, we had to make many choices, including the number of hidden neurons. Other choices to be made are the number of layers and type of layers. You might wonder how you should make these architectural choices. Unfortunately, there are no clear rules to follow here, and it often boils down to a lot of trial and error. It is recommended to explore what others have done with similar data sets and problems. Another best practice is to start with a relatively simple architecture and then add layers and tweak the network to test if performance increases.
We have a model now what?
This CNN should be able to run with the CIFAR-10 data set and provide reasonable results for basic classification tasks. However, do keep in mind this model is relatively simple, and its performance may not be as high as more complex architectures. The reason it’s called deep learning is because, in most cases, the more layers we have, i.e. the deeper and more sophisticated CNN architecture we use, the better the performance.
How can we judge a model’s performance? We can inspect a couple metrics produced during the training process to detect whether our model is underfitting or overfitting. To do that, we continue with the next steps in our Deep Learning workflow, Step 5. Choose a loss function and optimizer and Step 6. Train model.
- Artificial neural networks (ANN) are a machine learning technique based on a model inspired by groups of neurons in the brain.
- Convolution neural networks (CNN) are a type of ANN designed for image classification and object detection.
- The number of filters corresponds to the number of distinct features the layer is learning to recognise whereas the kernel size determines the level of features being captured.
- A CNN can consist of many types of layers including convolutional, pooling, flatten, and dense (fully connected) layers
- Convolutional layers are responsible for learning features from the input data.
- Pooling layers are often used to reduce the spatial dimensions of the data.
- The flatten layer is used to convert the multi-dimensional output of the convolutional and pooling layers into a flat vector.
- Dense layers are responsible for combining features learned by the previous layers to perform the final classification.
