Principal component analysis
Overview
Teaching: 90 min
Exercises: 40 minQuestions
What is principal component analysis (PCA) and when can it be used?
How can we perform a PCA in R?
How many principal components are needed to explain a significant amount of variation in the data?
How to interpret the output of PCA using loadings and principal components?
Objectives
Identify situations where PCA can be used to answer research questions using high-dimensional data.
Perform a PCA on high-dimensional data.
Select the appropriate number of principal components.
Interpret the output of PCA.
Introduction
If a dataset contains many variables ($p$), it is likely that some of these variables will be highly correlated. Variables may even be so highly correlated that they represent the same overall effect. Such datasets are challenging to analyse for several reasons, with the main problem being how to reduce dimensionality in the dataset while retaining the important features.
In this episode we will explore principal component analysis (PCA) as a popular method of analysing high-dimensional data. PCA is a statistical method which allows large datasets of correlated variables to be summarised into smaller numbers of uncorrelated principal components that explain most of the variability in the original dataset. As an example, PCA might reduce several variables representing aspects of patient health (blood pressure, heart rate, respiratory rate) into a single feature capturing an overarching “patient health” effect. This is useful from an exploratory point of view, discovering how variables might be associated and combined. The resulting principal component could also be used as an effect in further analysis (e.g. linear regression).
Challenge 1
Descriptions of three datasets and research questions are given below. For which of these might PCA be considered a useful tool for analysing data so that the research questions may be addressed?
- An epidemiologist has data collected from different patients admitted to hospital with infectious respiratory disease. They would like to determine whether length of stay in hospital differs in patients with different respiratory diseases.
- A scientist has assayed gene expression levels in 1000 cancer patients and has data from probes targeting different genes in tumour samples from patients. She would like to create new variables representing relative abundance of different groups of genes to i) find out if genes form subgroups based on biological function and ii) use these new variables in a linear regression examining how gene expression varies with disease severity.
- Both of the above.
Solution
In the first case, a regression model would be more suitable; perhaps a survival model. In the second example, PCA can help to identify modules of correlated features that explain a large amount of variation within the data.
Therefore the answer here is 2.
Principal component analysis
PCA transforms a dataset of continuous variables into a new set of uncorrelated variables called “principal components”. The first principal component derived explains the largest amount of the variability in the underlying dataset. The second principal component derived explains the second largest amount of variability in the dataset and so on. Once the dataset has been transformed into principal components, we can extract a subset of the principal components in order of the variance they explain (starting with the first principal component that by definition explains the most variability, and then the second), giving new variables that explain a lot of the variability in the original dataset. Thus, PCA helps us to produce a lower dimensional dataset while keeping most of the information in the original dataset.
To see what these new principal components may look like, the figure below shows the log-transformed prostate specific antigen (lpsa) versus cancer
volume (lcavol) data from the prostate data set introduced in Episode 1. Principal components are a collection of new, artificial data points, one for each individual observation called scores.
The red line on the plot represents the line passing through the scores (points) of the first principal component for each observation.
The angle that the first principal component line passes through the data points at is set to the direction with the highest
variability. The plotted first principal components can therefore be thought of reflecting the
effect in the data that has the highest variability. The second principal component explains the next highest amount of variability
in the data and is represented by the line perpendicular to the first (the green line). The second principal component can be thought of as
capturing the overall effect in the data that has the second-highest variability.
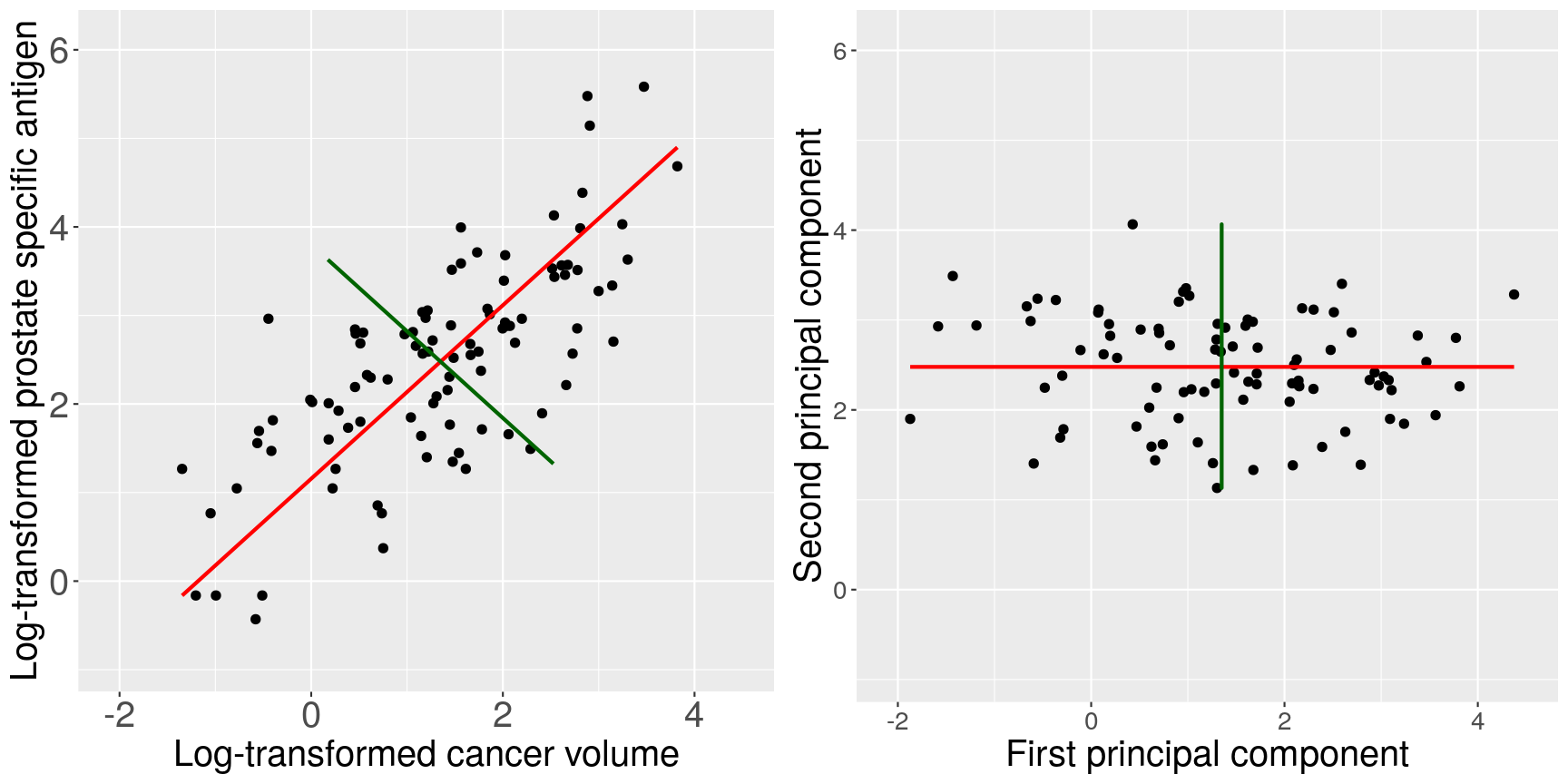
Scatter plots of the prostate data with the first principal component in red and second principal component in green.
The animation below illustrates how principal components are calculated from data. You can imagine that the black line is a rod and each red dashed line is a spring. The energy of each spring is proportional to its squared length. The direction of the first principal component is the one that minimises the total energy of all of the springs. In the animation below, the springs pull the rod, finding the direction of the first principal component when they reach equilibrium. We then use the length of the springs from the rod as the first principal component. This is explained in more detail on this Q&A website.
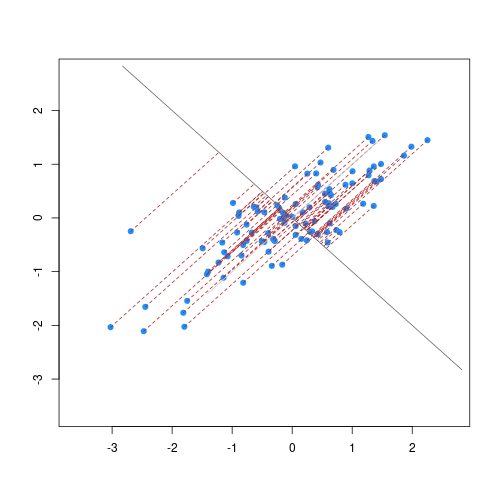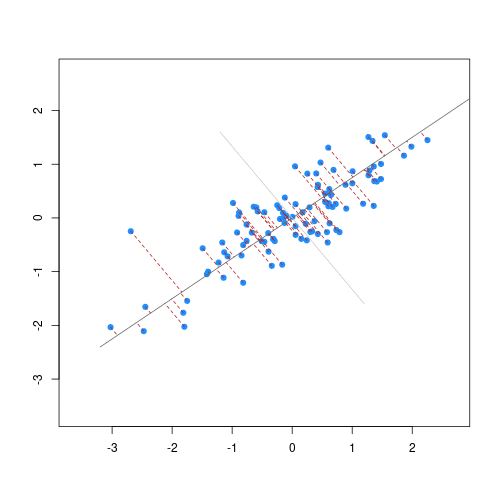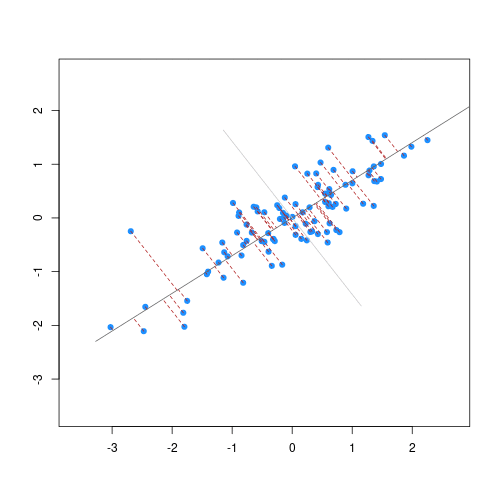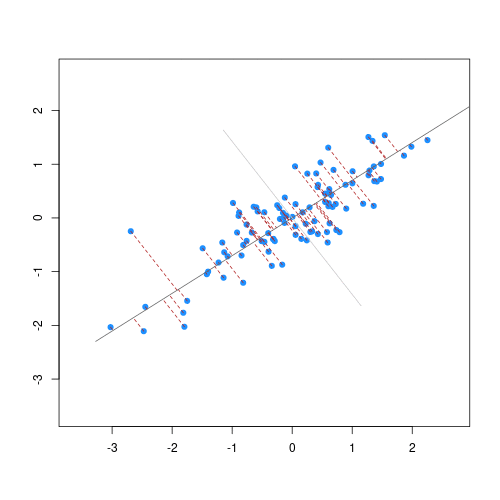
Animation showing the iterative process by which principal components are found. Data points are shown in blue, distances from the line as red dashed lines and the principal component is shown by a black line.
Mathematical description of PCA
Mathematically, each principal component is a linear combination of the variables in the dataset. That is, the first principal component values or scores, $Z_1$, are a linear combination of variables in the dataset, $X_1…X_p$, given by
\[Z_1 = a_{11}X_1 + a_{21}X_2 +....+a_{p1}X_p,\]where $a_{11}…a_{p1}$ represent principal component loadings.
In summary, the principal components’ values are called scores. The loadings can be thought of as the degree to which each original variable contributes to the principal component scores. In this episode, we will see how to perform PCA to summarise the information in high-dimensional datasets.
How do we perform a PCA?
To illustrate how to perform PCA initially, we revisit the low-dimensional prostate dataset.
The data come from a study which examined the
correlation between the level of prostate specific antigen and a number of
clinical measures in 97 men who were about to receive a radical prostatectomy.
The data have 97 rows and 9 columns.
The variables in the dataset (columns) are:
lcavol(log-transformed cancer volume),lweight(log-transformed prostate weight),lbph(log-transformed amount of benign prostate enlargement),svi(seminal vesicle invasion),lcp(log-transformed capsular penetration; amount of spread of cancer in outer walls of prostate),gleason(Gleason score; grade of cancer cells),pgg45(percentage Gleason scores 4 or 5),lpsa(log-transformed prostate specific antigen; level of PSA in blood).age(patient age in years).
We will perform PCA on the five continuous clinical variables in our dataset so that we can create fewer variables representing clinical markers of cancer progression.
First, we will examine the prostate dataset (originally part of the
lasso2 package):
library("here")
prostate <- readRDS(here("data/prostate.rds"))
head(prostate)
lcavol lweight age lbph svi lcp gleason pgg45 lpsa
1 -0.5798185 2.769459 50 -1.386294 0 -1.386294 6 0 -0.4307829
2 -0.9942523 3.319626 58 -1.386294 0 -1.386294 6 0 -0.1625189
3 -0.5108256 2.691243 74 -1.386294 0 -1.386294 7 20 -0.1625189
4 -1.2039728 3.282789 58 -1.386294 0 -1.386294 6 0 -0.1625189
5 0.7514161 3.432373 62 -1.386294 0 -1.386294 6 0 0.3715636
6 -1.0498221 3.228826 50 -1.386294 0 -1.386294 6 0 0.7654678
Note that each row of the dataset represents a single patient.
We will create a subset of the data including only the clinical variables we want to use in the PCA.
pros2 <- prostate[, c("lcavol", "lweight", "lbph", "lcp", "lpsa")]
head(pros2)
lcavol lweight lbph lcp lpsa
1 -0.5798185 2.769459 -1.386294 -1.386294 -0.4307829
2 -0.9942523 3.319626 -1.386294 -1.386294 -0.1625189
3 -0.5108256 2.691243 -1.386294 -1.386294 -0.1625189
4 -1.2039728 3.282789 -1.386294 -1.386294 -0.1625189
5 0.7514161 3.432373 -1.386294 -1.386294 0.3715636
6 -1.0498221 3.228826 -1.386294 -1.386294 0.7654678
Do we need to scale the data?
PCA derives principal components based on the variance they explain in the data. Therefore, we may need to apply some pre-processing to scale variables in our dataset if we want to ensure that each variable is considered equally by the PCA. Scaling is essential if we want to avoid the PCA ignoring variables that may be important to our analysis just because they take low values and have low variance. We do not need to scale if we want variables with low variance to carry less weight in the PCA.
In this example, we want each variable to be treated equally by the PCA since variables with lower values may be just as informative as variables with higher values. Let’s therefore investigate the variables in our dataset to see if we need to scale our variables first:
apply(pros2, 2, var)
lcavol lweight lbph lcp lpsa
1.389157 0.246642 2.104840 1.955102 1.332476
par(mfrow = c(1, 2))
hist(pros2$lweight)
hist(pros2$lbph)
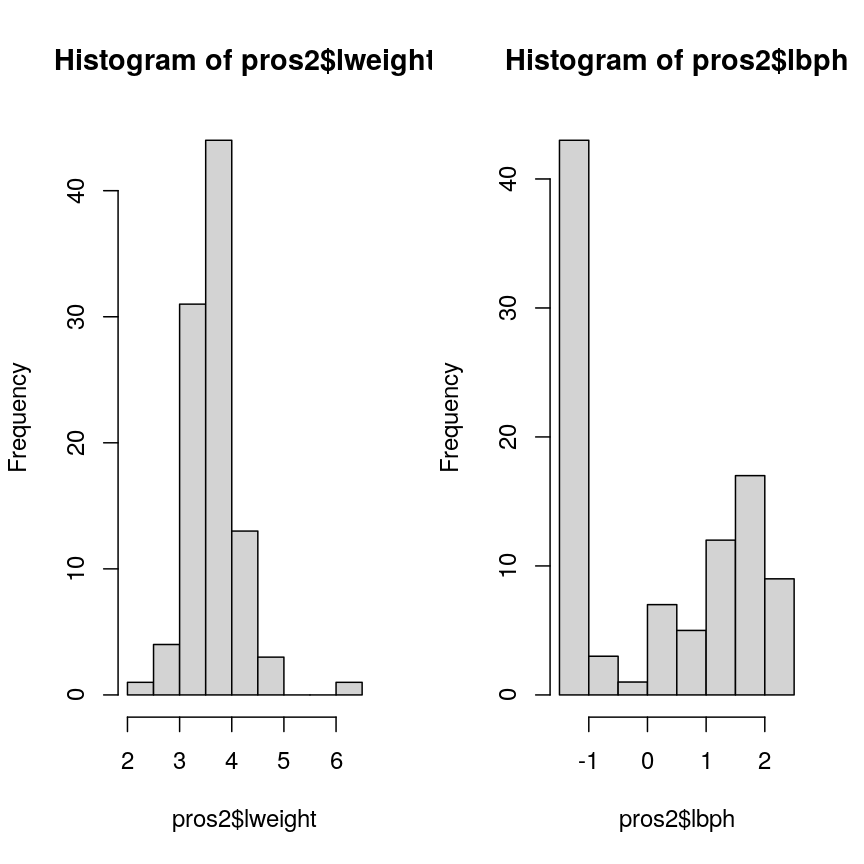
Histograms of two variables from the prostate data set.
Note that variance is greatest for lbph and lowest for lweight. Since we
want each of the variables to be treated equally in our PCA, but there are large differences in the variances of the variables, we need to scale each of the variables before including
them in a PCA to ensure that differences in variances
do not drive the calculation of principal components. In this example, we
standardise all five variables to have a mean of 0 and a standard
deviation of 1.
Challenge 2
- Why might it be necessary to standardise variables before performing a PCA?
Some ideas:
- To make the results of the PCA interesting.
- If you want to ensure that variables with different ranges of values contribute equally to analysis.
- To allow the feature matrix to be calculated faster, especially in cases where there are a lot of input variables.
- To allow both continuous and categorical variables to be included in the PCA.
- All of the above.
- Can you think of datasets where it might not be necessary to standardise variables?
Solution
Scaling the data isn’t guaranteed to make the results more interesting. It also won’t affect how quickly the output will be calculated, whether continuous and categorical variables are present or not.
We use scaling to ensure that features with different ranges of values have equal weighting in the resulting principal components (point 2).
You may not want to standardise datasets which contain continuous variables all measured on the same scale (e.g. gene expression data or RNA sequencing data). In this case, variables with very little sample-to-sample variability may represent only random noise, and standardising the data would give these extra weight in the PCA.
Performing PCA
Throughout this episode, we will carry out PCA using the Bioconductor package PCAtools.
This package provides several functions that are useful for exploring data via PCA and
producing useful figures and analysis tools. The package is made for the somewhat unusual
Bioconductor style of data tables (observations in columns, features in rows). When
using Bioconductor data sets and PCAtools, it is thus not necessary to transpose the data.
You can use the help files in the package documentation to find out about the pca()
function (type help("pca") or ?pca in R). Although we focus on PCA implementation using this package, there are several other
options for performing PCA, including a base R function, prcomp(). Equivalent functions and
output labels for the common implementations are summarised below.
| library::command() | Principal component scores | Loadings |
|---|---|---|
| stats::prcomp() | $x | $rotation |
| stats::princomp() | $scores | $loadings |
| PCAtools::pca() | $rotated | $loadings |
Let’s use the PCAtools package to perform PCA on the scaled prostate data. First, let’s load the PCAtools package.
library("PCAtools")
The input data (pros2) is in the form of a matrix and we need to take the transpose of this
matrix and convert it to a data frame for use within the PCAtools package. We set the scale = TRUE argument to standardise the variables to have a mean 0 and standard deviation of 1 as above.
pros2t <- data.frame(t(pros2)) # create transposed data frame
colnames(pros2t)<-seq(1:dim(pros2t)[2]) # rename columns for use within PCAtools
pmetadata= data.frame("M" = rep(1, dim(pros2t)[2]), row.names = colnames(pros2t)) # create fake metadata for use with PCA tools
## implement PCA
pca.pros <- pca(pros2t, scale = TRUE, center = TRUE, metadata = pmetadata)
summary(pca.pros)
Length Class Mode
rotated 5 data.frame list
loadings 5 data.frame list
variance 5 -none- numeric
sdev 5 -none- numeric
metadata 1 data.frame list
xvars 5 -none- character
yvars 97 -none- character
components 5 -none- character
How many principal components do we need?
We have calculated one principal component for each variable in the original dataset. How do we choose how many of these are necessary to represent the true variation in the data, without having extra components that are unnecessary?
Let’s look at the relative importance of (percentage of the variance explained by) the components:
prop.var <- round(pca.pros$variance, digits = 4)
prop.var
PC1 PC2 PC3 PC4 PC5
48.9767 27.3063 11.1094 8.0974 4.5101
This returns the proportion of variance in the data explained by each of the principal components. In this example, the first principal component, PC1, explains approximately 49% of variance in the data, PC2 27% of variance, PC3 a further 11%, PC4 approximately 8% and PC5 around 5%.
Let’s visualise this. A plot of the amount of variance accounted for by each principal component is also called a scree plot. Often, scree plots show a characteristic pattern where initially, the variance drops rapidly with each additional principal component. But then there is an “elbow” after which the variance decreases more slowly. The total variance explained up to the elbow point is sometimes interpreted as structural variance that is relevant and should be retained versus noise which may be discarded after the elbow.
We can create a scree plot using the PCAtools function screeplot():
screeplot(pca.pros, axisLabSize = 5, titleLabSize = 8,
drawCumulativeSumLine = FALSE, drawCumulativeSumPoints = FALSE) +
geom_line(aes(x = 1:length(pca.pros$components), y = as.numeric(pca.pros$variance)))
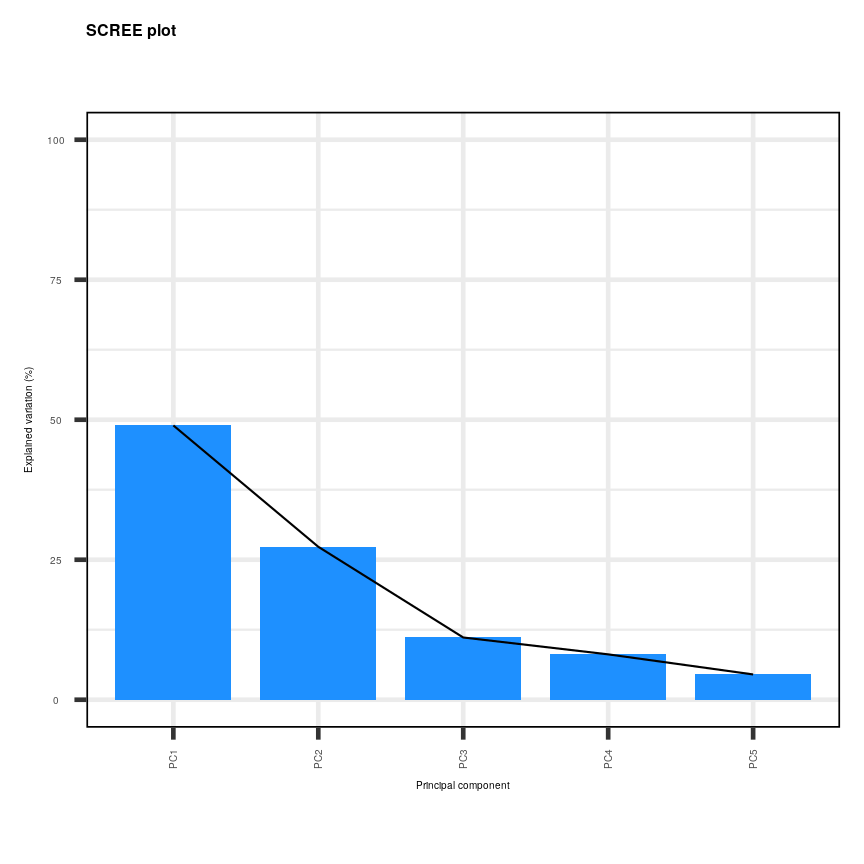
Scree plot showing the percentage of the variance explained by the principal components calculated from the prostate data.
The scree plot shows that the first principal component explains most of the variance in the data (>50%) and each subsequent principal component explains less and less of the total variance. The first two principal components explain >70% of variance in the data.
Selecting a subset of principal components results in loss of information from the original dataset but selecting principal components to summarise the majority of the information in the original dataset is useful from a practical dimension reduction perspective. There are no clear guidelines on how many principal components should be included in PCA. We often look at the ‘elbow’ on the scree plot as an indicator that the addition of principal components does not drastically contribute to explaining the remaining variance. In this case, the ‘elbow’ of the scree plot appears to be at the third principal component. We may therefore conclude that three principal components are sufficient to explain the majority of the variability in the original dataset. We may also choose another criterion, such as an arbitrary cut-off for the proportion of the variance explained compared to other principal components. Essentially, the criterion used to select principal components should be determined based on what is deemed a sufficient level of information retention for a specific dataset and question.
Loadings and principal component scores
Most PCA functions will produce two main output matrices: the principal component scores and the loadings. The matrix of principal component scores has as many rows as there were observations in the input matrix. These scores are what is usually visualised or used for down-stream analyses. The matrix of loadings (also called rotation matrix) has as many rows as there are features in the original data. It contains information about how the (usually centered and scaled) original data relate to the principal component scores.
We can print the loadings for the PCAtools implementation using
pca.pros$loadings
PC1 PC2 PC3 PC4 PC5
lcavol 0.5616465 -0.23664270 0.01486043 0.22708502 -0.75945046
lweight 0.2985223 0.60174151 -0.66320198 -0.32126853 -0.07577123
lbph 0.1681278 0.69638466 0.69313753 0.04517286 -0.06558369
lcp 0.4962203 -0.31092357 0.26309227 -0.72394666 0.25253840
lpsa 0.5665123 -0.01680231 -0.10141557 0.56487128 0.59111493
The principal component scores are obtained by carrying out matrix multiplication of the (usually centered and scaled) original data times the loadings. The following callout demonstrates this.
Computing a PCA “by hand”
The rotation matrix obtained in a PCA is identical to the eigenvectors of the covariance matrix of the data. Multiplying these with the (centered and scaled) data yields the principal component scores:
pros2.scaled <- scale(pros2) # centre and scale the prostate data pros2.cov <- cov(pros2.scaled) # generate covariance matrix pros2.covlcavol lweight lbph lcp lpsa lcavol 1.0000000 0.1941283 0.027349703 0.675310484 0.7344603 lweight 0.1941283 1.0000000 0.434934636 0.100237795 0.3541204 lbph 0.0273497 0.4349346 1.000000000 -0.006999431 0.1798094 lcp 0.6753105 0.1002378 -0.006999431 1.000000000 0.5488132 lpsa 0.7344603 0.3541204 0.179809410 0.548813169 1.0000000pros2.eigen <- eigen(pros2.cov) # preform eigen decomposition pros2.eigen # The slot $vectors = rotation of the PCAeigen() decomposition $values [1] 2.4488355 1.3653171 0.5554705 0.4048702 0.2255067 $vectors [,1] [,2] [,3] [,4] [,5] [1,] -0.5616465 0.23664270 0.01486043 0.22708502 0.75945046 [2,] -0.2985223 -0.60174151 -0.66320198 -0.32126853 0.07577123 [3,] -0.1681278 -0.69638466 0.69313753 0.04517286 0.06558369 [4,] -0.4962203 0.31092357 0.26309227 -0.72394666 -0.25253840 [5,] -0.5665123 0.01680231 -0.10141557 0.56487128 -0.59111493# generate principal component scores by by hand, using matrix multiplication my.pros2.pcs <- pros2.scaled %*% pros2.eigen$vectors # compare results par(mfrow=c(1,2)) plot(pca.pros$rotated[,1:2], main="PCAtools") abline(h=0, v=0, lty=2) plot(my.pros2.pcs[,1:2], main="\"By hand\"", xlab="PC1", ylab="PC2") abline(h=0, v=0, lty=2)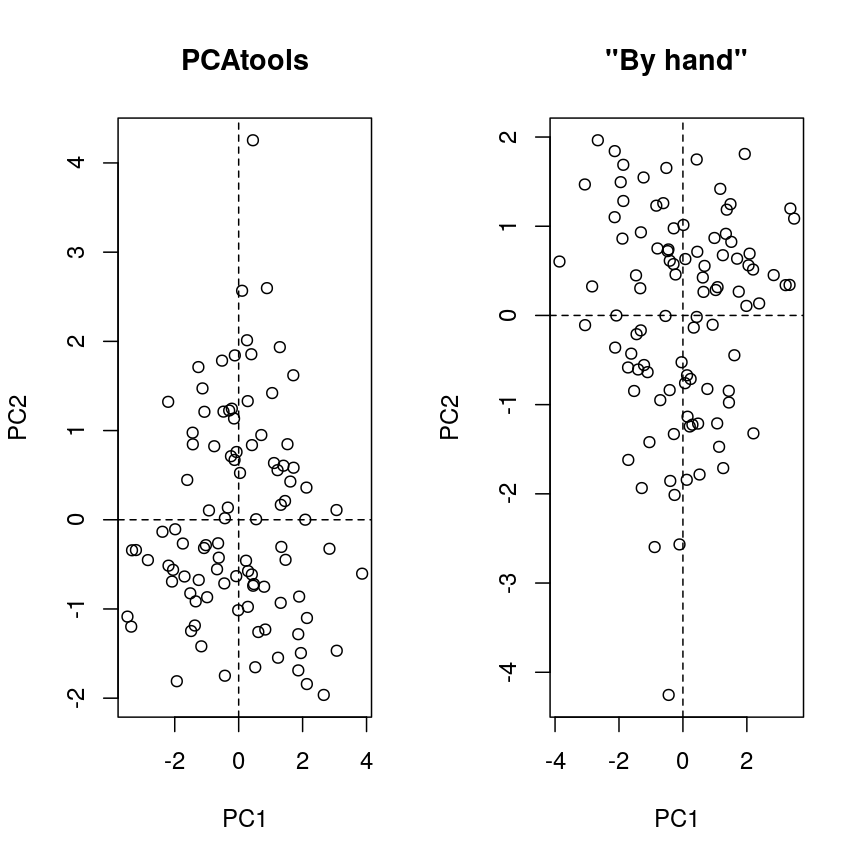
Scatter plots of the second versus first principal components calculated by prcomp() (left) and by hand (right).
par(mfrow=c(1,1)) # Note that the axis orientations may be swapped but the relative positions of the dots should be the same in both plots.
One way to visualise how principal components relate to the original variables
is by creating a biplot. Biplots usually show two principal components plotted
against each other. Observations are sometimes labelled with numbers. The
contribution of each original variable to the principal components displayed
is then shown by arrows (generated from those two columns of the rotation matrix that
correspond to the principal components shown). See help("PCAtools::biplot") for
arguments and their meaning. For instance, lab or colBy may be useful.
Note that there are several biplot
implementations in different R libraries. It is thus a good idea to specify
the desired package when calling biplot(). A biplot of the first two principal
components can be generated as follows:
PCAtools::biplot(pca.pros)
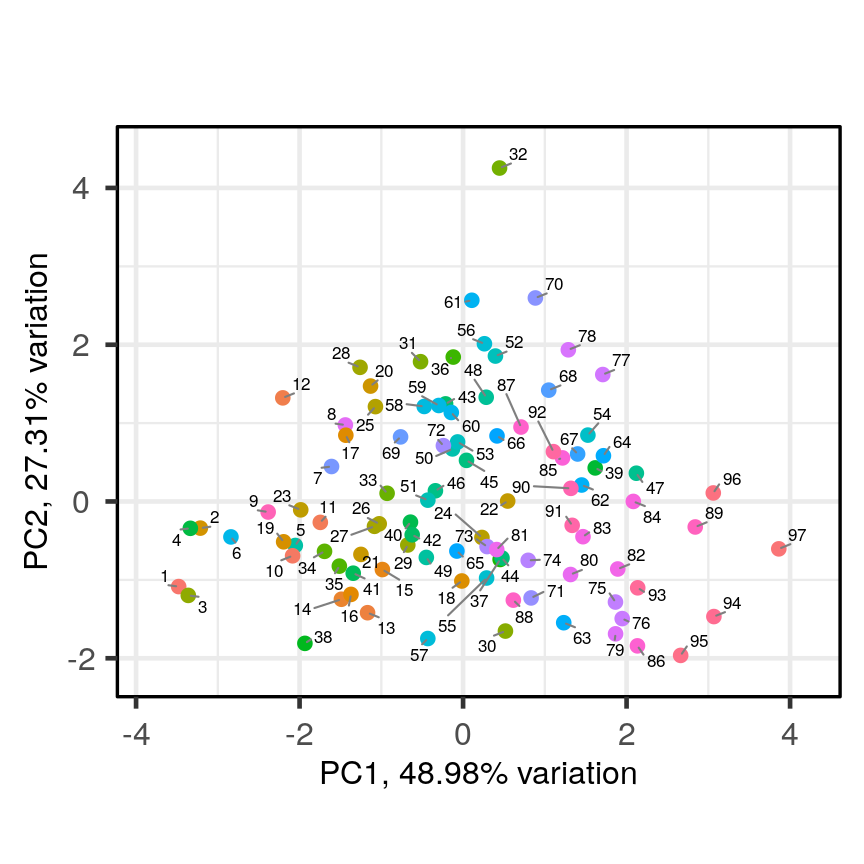
Scatter plot of the first two principal components with observations numerically labelled.
This biplot shows the position of each patient on a 2-dimensional plot where
loadings can be observed via the red arrows associated with each of
the variables. The variables lpsa, lcavol and lcp are associated with
positive values on PC1 while positive values on PC2 are associated with the
variables lbph and lweight. The length of the arrows indicates how much
each variable contributes to the calculation of each principal component.
The left and bottom axes show normalised principal component scores. The axes
on the top and right of the plot are used to interpret the loadings, where
loadings are scaled by the standard deviation of the principal components
(pca.pros$sdev) times the square root the number of observations.
Advantages and disadvantages of PCA
Advantages:
- It is a relatively easy to use and popular method.
- Various software/packages are available to run a PCA.
- The calculations used in a PCA are simple to understand compared to other methods for dimension reduction.
Disadvantages:
- It assumes that variables in a dataset are correlated.
- It is sensitive to the scale at which input variables are measured. If input variables are measured at different scales, the variables with large variance relative to the scale of measurement will have greater impact on the principal components relative to variables with smaller variance. In many cases, this is not desirable.
- It is not robust against outliers, meaning that very large or small data points can have a large effect on the output of the PCA.
- PCA assumes a linear relationship between variables which is not always a realistic assumption.
- It can be difficult to interpret the meaning of the principal components, especially when including them in further analyses (e.g. inclusion in a linear regression).
Using PCA to analyse gene expression data
The dataset we will be analysing in this lesson includes two subsets of data:
- a matrix of gene expression data showing microarray results for different probes used to examine gene expression profiles in 91 different breast cancer patient samples.
- metadata associated with the gene expression results detailing information from patients from whom samples were taken.
In this section, we will work through Challenges and you will apply your own PCA to the high-dimensional gene expression data using what we have learnt so far.
We will first load the microarray breast cancer gene expression data and associated metadata, downloaded from the Gene Expression Omnibus.
library("SummarizedExperiment")
cancer <- readRDS(here("data/cancer_expression.rds"))
mat <- assay(cancer)
metadata <- colData(cancer)
head(mat)
head(metadata)
# Check that column names and row names match, if they do should return TRUE
all(colnames(mat) == rownames(metadata))
[1] TRUE
The mat variable contains a matrix of gene expression profiles for each sample.
Rows represent gene expression measurements and columns represent samples. The
metadata variable contains the metadata associated with the gene expression
data including the name of the study from which data originate, the age of the
patient from which the sample was taken, whether or not an oestrogen receptor
was involved in their cancer and the grade and size of the cancer for each
sample (represented by rows).
Microarray data are difficult to analyse for several reasons. Firstly, formulating a research question using microarray data can be difficult, especially if not much is known a priori about which genes code for particular phenotypes of interest. Secondly, they are typically high-dimensional and therefore are subject to the same difficulties associated with analysing high-dimensional data. Finally, exploratory analysis, which can be used to help formulate research questions and display relationships, is difficult using microarray data due to the number of potentially interesting response variables (i.e. expression data from probes targeting different genes).
If researchers hypothesise that groups of genes (e.g. biological pathways) may be associated with different phenotypic characteristics of cancers (e.g. histologic grade, tumour size), using statistical methods that reduce the number of columns in the microarray matrix to a smaller number of dimensions representing groups of genes would help visualise the data and address research questions regarding the effect different groups of genes have on disease progression.
Using PCAtools, we will perform PCA on the cancer
gene expression data, plot the amount of variation in the data explained by
each principal component and plot the most important principal components
against each other as well as understanding what each principal component
represents.
Challenge 3
Apply a PCA to the cancer gene expression data using the
pca()function fromPCAtools.Let us assume we only care about the principal components accounting for the top 80% of the variance in the dataset. Use the
removeVarargument inpca()to remove the principal components accounting for the bottom 20%.As in the example using
prostatedata above, examine the first 5 rows and columns of rotated data and loadings from your PCA.Solution
pc <- pca(mat, metadata = metadata) # implement a PCA # We can check the scree plot to see that many principal components explain a very small amount of # the total variance in the data # Let's remove the principal components with lowest 20% of the variance pc <- pca(mat, metadata = metadata, removeVar = 0.2) # Explore other arguments provided in pca pc$rotated[1:5, 1:5] # obtain the first 5 principal component scores for the first 5 observationsPC1 PC2 PC3 PC4 PC5 GSM65752 -29.79105 43.866788 3.255903 -40.663138 15.3427597 GSM65753 -37.33911 -15.244788 -4.948201 -6.182795 9.4725870 GSM65755 -29.41462 7.846858 -22.880525 -16.149669 22.3821009 GSM65757 -33.35286 1.343573 -22.579568 2.200329 15.0082786 GSM65758 -40.51897 -8.491125 5.288498 14.007364 0.8739772pc$loadings[1:5, 1:5] # obtain the first 5 principal component loadings for the first 5 featuresPC1 PC2 PC3 PC4 PC5 206378_at -0.0024680993 -0.053253543 -0.004068209 0.04068635 0.015078376 205916_at -0.0051557973 0.001315022 -0.009836545 0.03992371 0.038552048 206799_at 0.0005684075 -0.050657061 -0.009515725 0.02610233 0.006208078 205242_at 0.0130742288 0.028876408 0.007655420 0.04449641 -0.001061205 206509_at 0.0019031245 -0.054698479 -0.004667356 0.01566468 0.001306807which.max(pc$loadings[, 1]) # index of the maximal loading for the first principal component[1] 49# principal component loadings for the feature # with the maximal loading on the first principal component: pc$loadings[which.max(pc$loadings[, 1]), ]PC1 PC2 PC3 PC4 PC5 215281_x_at 0.03752947 -0.007369379 0.006243377 -0.008242589 -0.004783206 PC6 PC7 PC8 PC9 PC10 215281_x_at 0.01194012 -0.002822407 -0.01216792 0.001137451 -0.0009056616 PC11 PC12 PC13 PC14 PC15 215281_x_at -0.00196034 -0.0001676705 0.00699201 -0.002897995 -0.0005044658 PC16 PC17 PC18 PC19 PC20 215281_x_at -0.0004547916 0.002277035 -0.006199078 0.002708574 -0.006217326 PC21 PC22 PC23 PC24 PC25 215281_x_at 0.00516745 0.007625912 0.003434534 0.005460017 0.001477415 PC26 PC27 PC28 PC29 PC30 215281_x_at 0.002350428 0.0007183107 -0.0006195515 0.0006349803 0.00413627 PC31 PC32 PC33 PC34 PC35 215281_x_at 0.0001322301 0.003182956 -0.002123462 -0.001042769 -0.001729869 PC36 PC37 PC38 PC39 PC40 215281_x_at -0.006556369 0.005766949 0.002537993 -0.0002846248 -0.00018195 PC41 PC42 PC43 PC44 PC45 215281_x_at -0.0007970789 0.003888626 -0.008210075 -0.0009570174 0.0007998935 PC46 PC47 PC48 PC49 PC50 215281_x_at -0.0006931441 -0.005717836 0.005189649 0.002591188 0.0007810259 PC51 PC52 PC53 PC54 PC55 215281_x_at 0.006610815 0.005371134 -0.001704796 -0.002286475 0.001365417 PC56 PC57 PC58 PC59 PC60 215281_x_at 0.003529892 0.0003375981 0.009895923 -0.001564423 -0.006989092 PC61 PC62 PC63 PC64 PC65 215281_x_at 0.000971273 0.001345406 -0.003575415 -0.0005588113 0.006516669 PC66 PC67 PC68 PC69 PC70 215281_x_at -0.008770186 0.006699641 0.01284606 -0.005041574 0.007845653 PC71 PC72 PC73 PC74 PC75 215281_x_at 0.003964697 -0.01104367 -0.001506485 -0.001583824 0.003798343 PC76 PC77 PC78 PC79 PC80 215281_x_at 0.004817252 -0.001290033 -0.004402926 -0.003440367 -0.0001646198 PC81 PC82 PC83 PC84 PC85 215281_x_at 0.003923775 0.003179556 -0.0004388192 9.664648e-05 0.003501335 PC86 PC87 PC88 PC89 PC90 215281_x_at -0.00112973 0.006489667 -0.0005039785 -0.004296355 -0.002751513 PC91 215281_x_at -0.00383085which.max(pc$loadings[, 2]) # index of the maximal loading for the second principal component[1] 27# principal component loadings for the feature # with the maximal loading on the second principal component: pc$loadings[which.max(pc$loadings[, 2]), ]PC1 PC2 PC3 PC4 PC5 211122_s_at 0.01649085 0.05090275 -0.003378728 0.05178144 -0.003742393 PC6 PC7 PC8 PC9 PC10 211122_s_at -0.00543753 -0.03522848 -0.006333521 0.01575401 0.004732546 PC11 PC12 PC13 PC14 PC15 211122_s_at 0.004687599 -0.01349892 0.005207937 -0.01731898 0.02323893 PC16 PC17 PC18 PC19 PC20 211122_s_at -0.02069509 0.01477432 0.005658529 0.02667751 -0.01333503 PC21 PC22 PC23 PC24 PC25 211122_s_at -0.003254036 0.003572342 0.01416779 -0.005511838 -0.02582847 PC26 PC27 PC28 PC29 PC30 PC31 211122_s_at 0.03405417 -0.01797345 0.01826328 0.005123959 0.01300763 0.0127127 PC32 PC33 PC34 PC35 PC36 211122_s_at 0.002477672 0.01933214 0.03017661 -0.01935071 -0.01960912 PC37 PC38 PC39 PC40 PC41 211122_s_at 0.004411188 -0.01263612 -0.02019279 -0.01441513 -0.0310399 PC42 PC43 PC44 PC45 PC46 211122_s_at -0.02540426 0.0007949801 -0.00200195 -0.01748543 0.006881834 PC47 PC48 PC49 PC50 PC51 211122_s_at 0.006690698 -0.004000732 -0.02747926 -0.006963189 -0.02232332 PC52 PC53 PC54 PC55 PC56 211122_s_at -0.0003089115 -0.01604491 0.005649511 -0.02629501 0.02332997 PC57 PC58 PC59 PC60 PC61 211122_s_at -0.01248022 -0.01563245 0.005369433 0.009445262 -0.005209349 PC62 PC63 PC64 PC65 PC66 211122_s_at 0.01787645 0.01629425 0.02457665 -0.02384242 0.002814479 PC67 PC68 PC69 PC70 PC71 211122_s_at 0.0004584731 0.007939733 -0.009554166 -0.003967123 0.01825668 PC72 PC73 PC74 PC75 PC76 211122_s_at -0.00580374 -0.02236727 0.001295688 -0.02264723 0.006855855 PC77 PC78 PC79 PC80 PC81 211122_s_at 0.004995447 -0.008404118 0.00442875 -0.001027912 0.006104406 PC82 PC83 PC84 PC85 PC86 211122_s_at -0.01988441 0.009667348 -0.008248781 0.01198369 0.01221713 PC87 PC88 PC89 PC90 PC91 211122_s_at -0.003864842 -0.02876816 -0.01771452 -0.02164973 0.004593411The function
pca()is used to perform PCA, and uses as input a matrix (mat) containing continuous numerical data in which rows are data variables and columns are samples, andmetadataassociated with the matrix in which rows represent samples and columns represent data variables. It has options to centre or scale the input data before a PCA is performed, although in this case gene expression data do not need to be transformed prior to PCA being carried out as variables are measured on a similar scale (values are comparable between rows). The output of thepca()function includes a lot of information such as loading values for each variable (loadings), principal component scores (rotated) and the amount of variance in the data explained by each principal component.Rotated data shows principal component scores for each sample and each principal component. Loadings the contribution each variable makes to each principal component.
Scaling variables for PCA
When running
pca()above, we kept the default setting,scale=FALSE. That means genes with higher variation in their expression levels should have higher loadings, which is what we are interested in. Whether or not to scale variables for PCA will depend on your data and research question.Note that this is different from normalising gene expression data. Gene expression data have to be normalised before donwstream analyses can be carried out. This is to reduce technical and other potentially confounding factors. We assume that the expression data we use had been normalised previously.
Choosing how many components are important to explain the variance in the data
As in the example using the prostate dataset, we can use a scree plot to
compare the proportion of variance in the data explained by each principal
component. This allows us to understand how much information in the microarray
dataset is lost by projecting the observations onto the first few principal
components and whether these principal components represent a reasonable
amount of the variation. The proportion of variance explained should sum to one.
Challenge 4
This time using the
screeplot()function inPCAtools, create a scree plot to show proportion of variance explained by the first 20 principal component (hint:components = 1:20). Explain the output of the scree plot in terms of proportion of the variance in the data explained by each principal component.Solution
pc <- pca(mat, metadata = metadata) screeplot(pc, components = 1:20) + ylim(0, 80)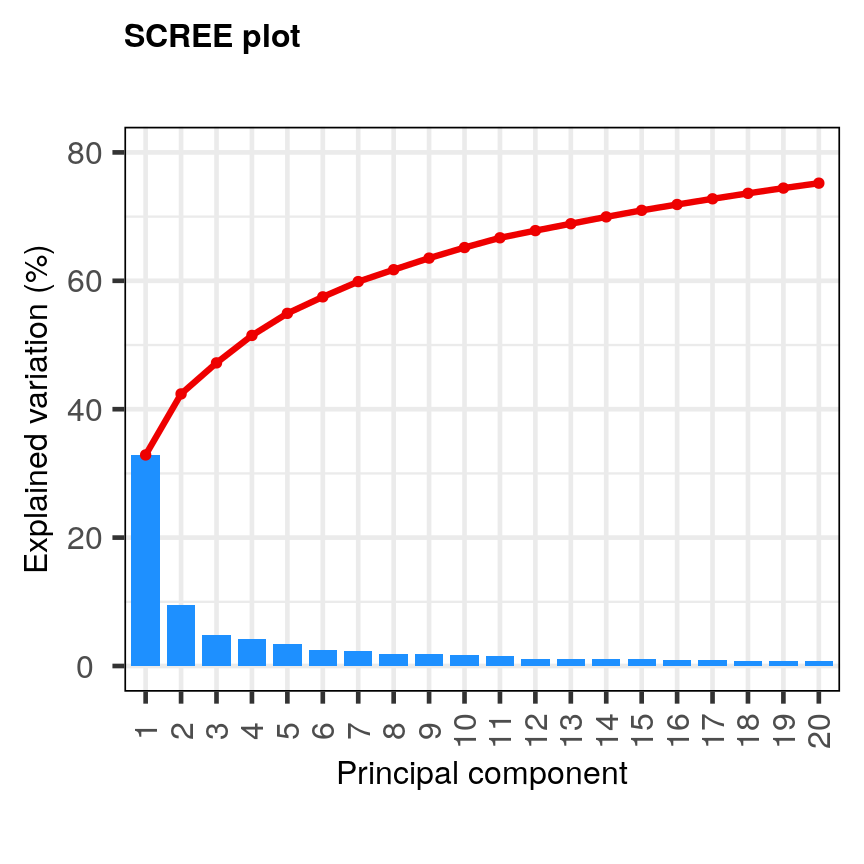
A scree plot of the gene expression data.
The first principal component explains around 33% of the variance in the microarray data, the first 4 principal components explain around 50%, and 20 principal components explain around 75%. Many principal components explain very little variation. A first ‘elbow’ appears to be around 4-5 principal components, indicating that this may be a suitable number of principal components. However, these principal components cumulatively explain only 51-55% of the variance in the dataset. Although the fact we are able to summarise most of the information in the complex dataset in 4-5 principal components may be a useful result, we may opt to retain more principal components (for example, 20) to capture more of the variability in the dataset depending on research question. A second ‘elbow’ around 12 principal components may provide a good middleground. Note that first principal component (PC1) explains more variation than other principal components (which is always the case in PCA). The scree plot shows that the first principal component only explains ~33% of the total variation in the microarray data and many principal components explain very little variation. The red line shows the cumulative percentage of explained variation with increasing principal components.
Note that in this case 18 principal components are needed to explain over 75% of variation in the data. This is not an unusual result for complex biological datasets including genetic information as clear relationships between groups are sometimes difficult to observe in the data. The scree plot shows that using a PCA we have reduced 91 predictors to 18 in order to explain a significant amount of variation in the data. See additional arguments in scree plot function for improving the appearance of the plot.
Investigating the principal components
Once the most important principal components have been identified using
screeplot() and explored, these can be explored in more detail by plotting principal components
against each other and highlighting points based on variables in the metadata.
This will allow any potential clustering of points according to demographic or
phenotypic variables to be seen.
We can use biplots to look for patterns in the output from the PCA. Note that there
are two functions called biplot(), one in the package PCAtools and one in
stats. Both functions produce biplots but their scales are different!
Challenge 5
Create a biplot of the first two principal components from your PCA using
biplot()function inPCAtools. Seehelp("PCAtools::biplot")for arguments and their meaning. For instance,laborcolbymay be useful.Examine whether the data appear to form clusters. Explain your results.
Solution
PCAtools::biplot(pc, lab = NULL, colby = 'Grade', legendPosition = 'top')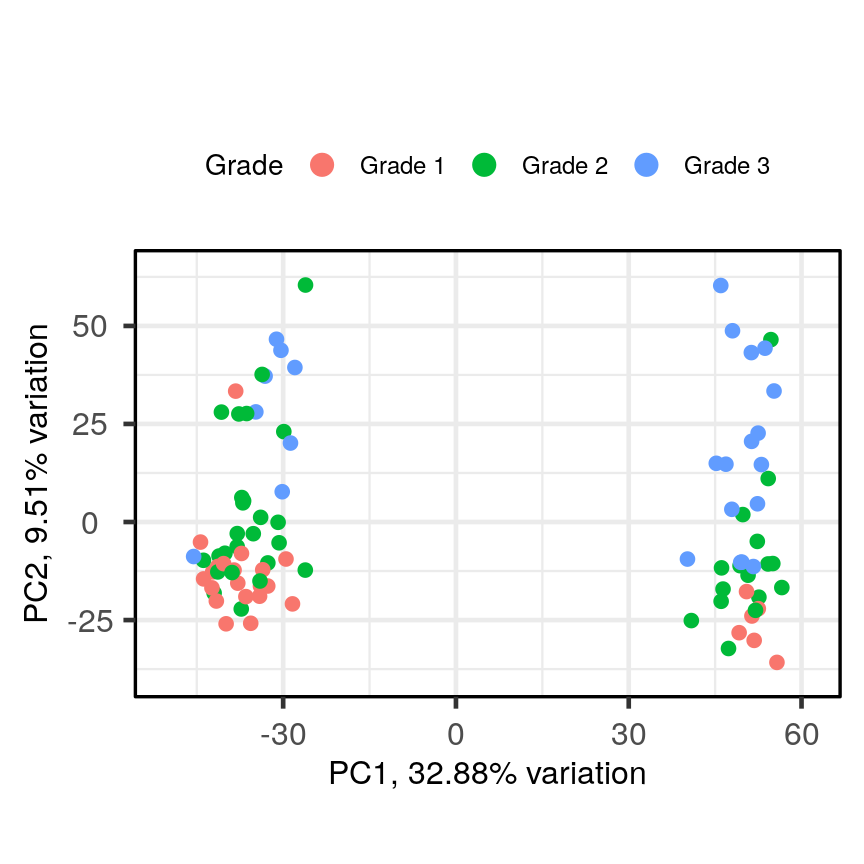
A biplot of PC2 against PC1 in the gene expression data, coloured by Grade.
The biplot shows the position of patient samples relative to PC1 and PC2 in a 2-dimensional plot. Note that two groups are apparent along the PC1 axis according to expressions of different genes while no separation can be seem along the PC2 axis. Labels of patient samples are automatically added in the biplot. Labels for each sample are added by default, but can be removed if there is too much overlap in names. Note that
PCAtoolsdoes not scale biplot in the same way as biplot using thestatspackage.
Let’s consider this biplot in more detail, and also display the loadings:
Challenge 6
Use
colbyandlabarguments inbiplot()to explore whether these two groups may cluster by patient age or by whether or not the sample expresses the oestrogen receptor gene (ER+ or ER-).Note: You may see a warning about
ggrepel. This happens when there are many labels but little space for plotting. This is not usually a serious problem - not all labels will be shown.Solution
PCAtools::biplot(pc, lab = paste0(pc$metadata$Age,'years'), colby = 'ER', legendPosition = 'right')Warning: ggrepel: 36 unlabeled data points (too many overlaps). Consider increasing max.overlaps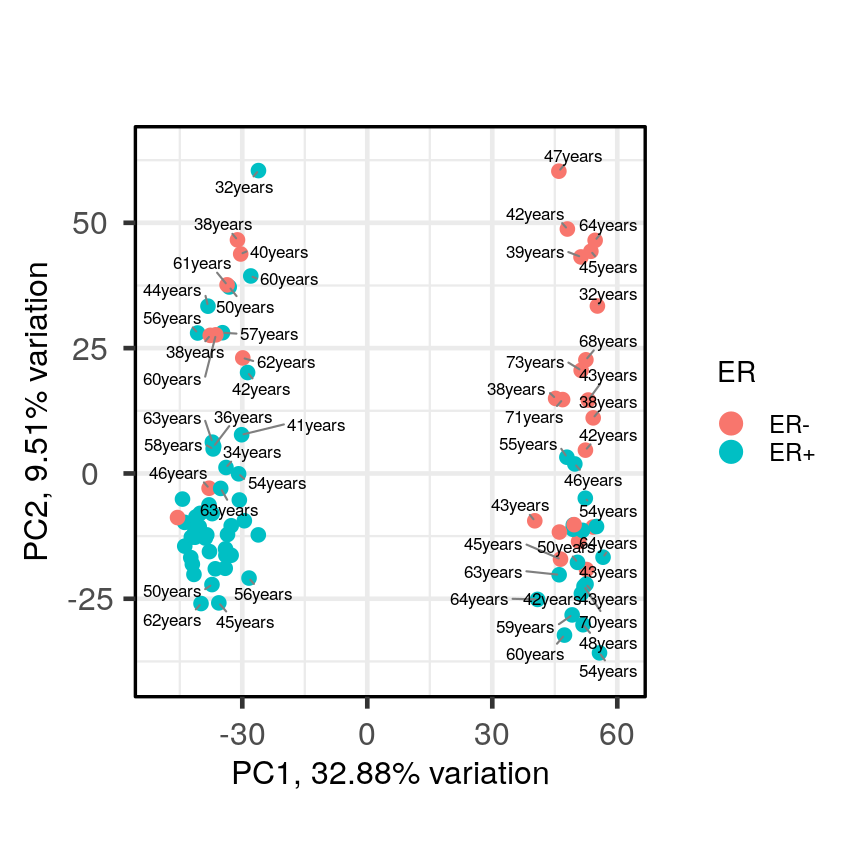
A biplot of PC2 against PC1 in the gene expression data, coloured by ER status with patient ages overlaid.
It appears that one cluster has more ER+ samples than the other group.
So far, we have only looked at a biplot of PC1 versus PC2 which only gives part
of the picture. The pairplots() function in PCAtools can be used to create
multiple biplots including different principal components.
pairsplot(pc)
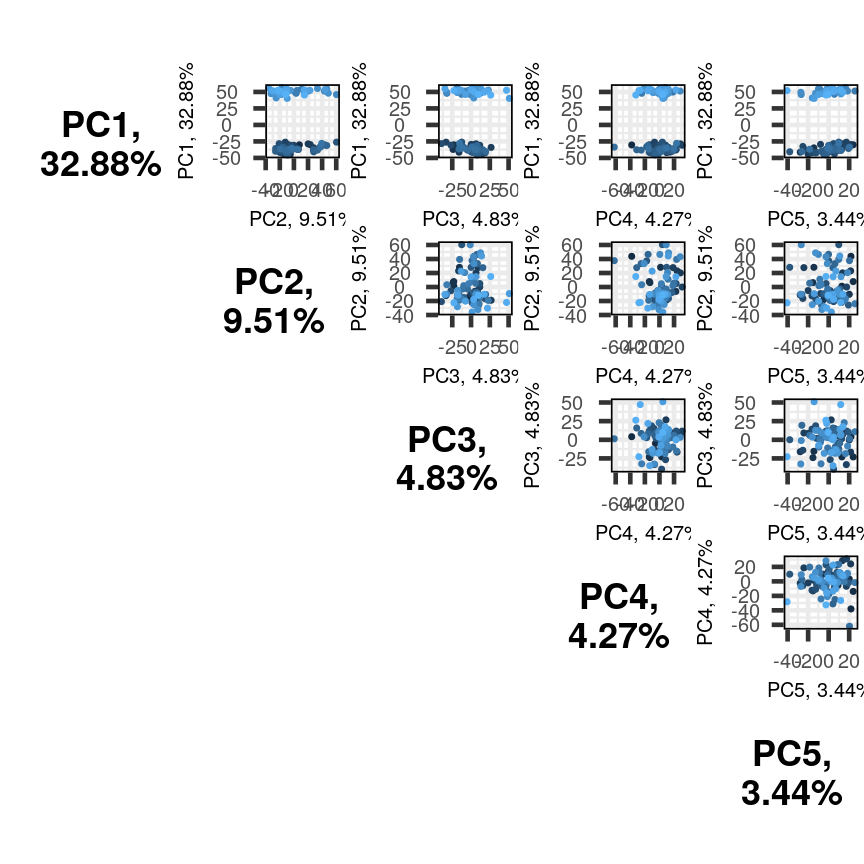
Multiple biplots produced by pairsplot().
The plots show two apparent clusters involving the first principal component
only. No other clusters are found involving other principal components. Each dot
is coloured differently along a gradient of blues. This can potentially help identifying
the same observation/individual in several panels. Here too, the argument colby allows
you to set custom colours.
Finally, it can sometimes be of interest to compare how certain variables contribute
to different principal components. This can be visualised with plotloadings() from
the PCAtools package. The function checks the range of loadings for each
principal component specified (default: first five principal components). It then selects the features
in the top and bottom 5% of these ranges and displays their loadings. This behaviour
can be adjusted with the rangeRetain argument, which has 0.1 as the default value (i.e.
5% on each end of the range). NB, if there are too many labels to be plotted, you will see
a warning. This is not a serious problem.
plotloadings(pc, c("PC1"), rangeRetain = 0.1)
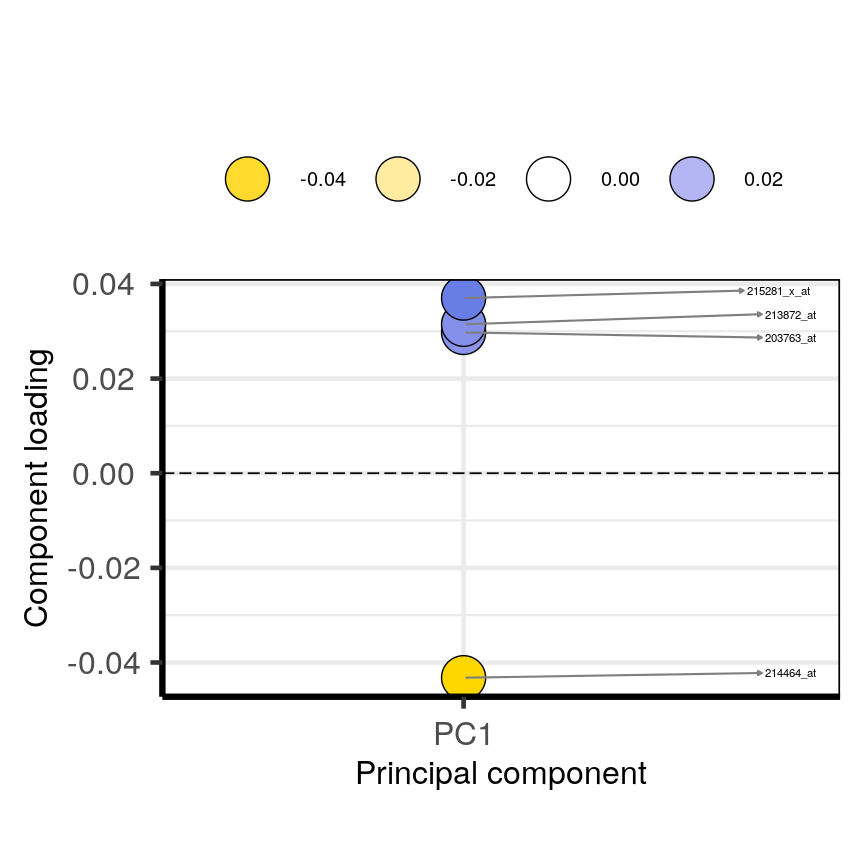
Plot of the features in the top and bottom 5 % of the loadings range for the first principal component.
plotloadings(pc, c("PC2"), rangeRetain = 0.1)
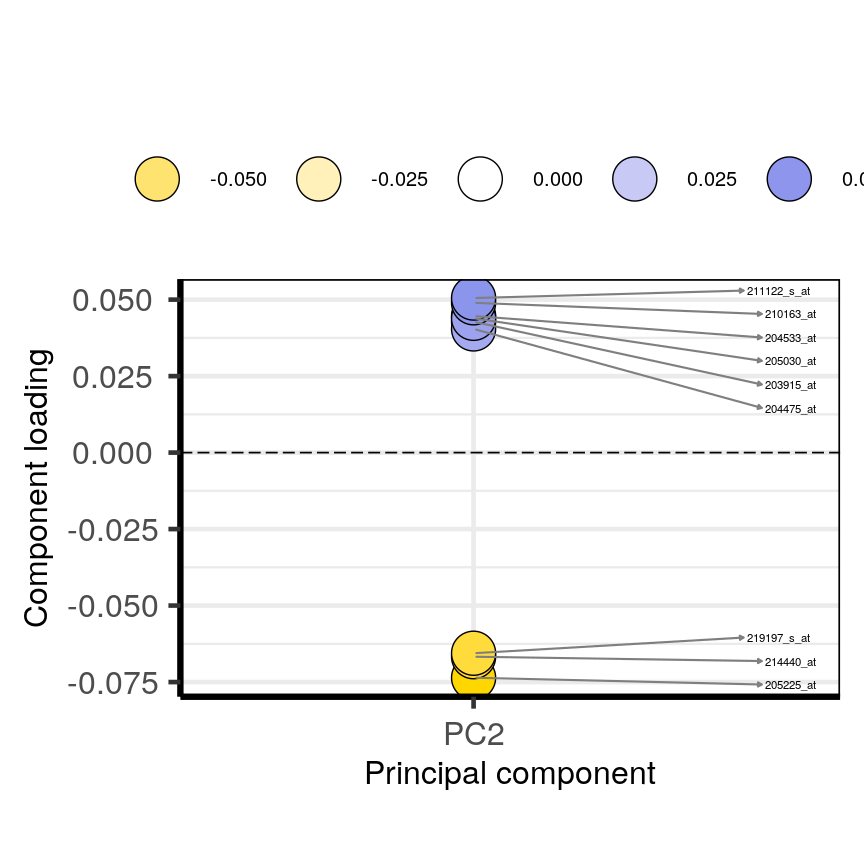
Plot of the features in the top and bottom 5 % of the loadings range for the second principal component.
plotloadings(pc, c("PC1", "PC2"), rangeRetain = 0.1)
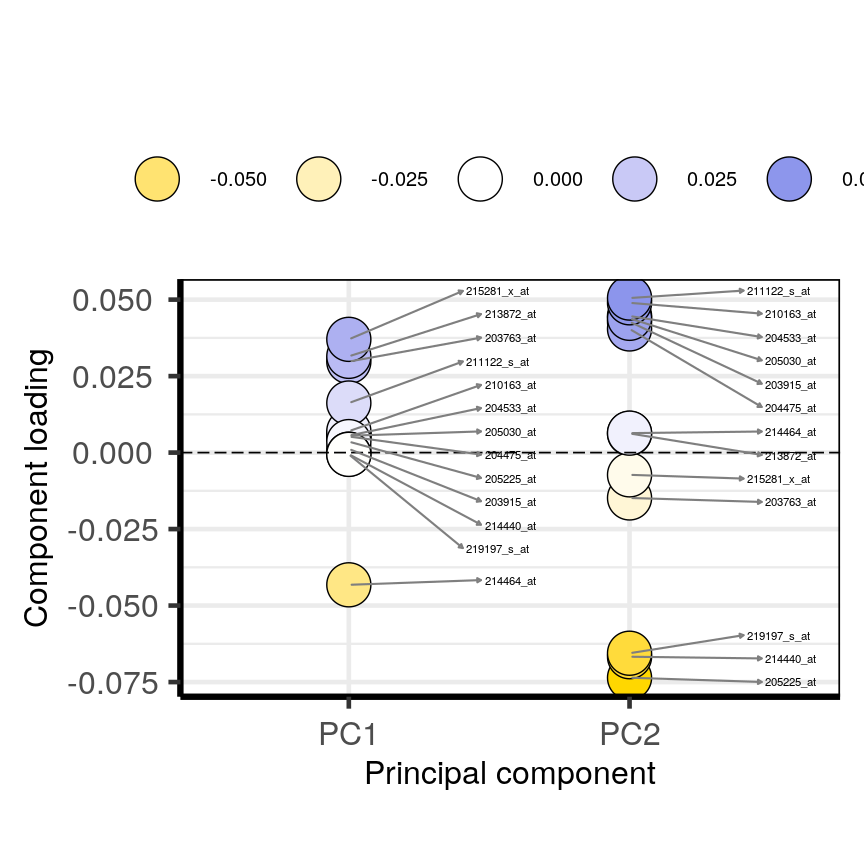
Plot of the features in the top and bottom 5 % of the loadings range for the either the first or second principal components.
You can see how the third code line produces more dots, some of which do not have extreme loadings. This is because all loadings selected for any principal component are shown for all other principal components. For instance, it is plausible that features which have high loadings on PC1 may have lower ones on PC2.
Using PCA output in further analysis
The output of PCA can be used to interpret data or can be used in further analyses. For example, the PCA outputs new variables (principal components) which represent several variables in the original dataset. These new variables are useful for further exploring data, for example, comparing principal component scores between groups or including the new variables in linear regressions. Because the principal components are uncorrelated (and independent) they can be included together in a single linear regression.
Principal component regression
PCA is often used to reduce large numbers of correlated variables into fewer uncorrelated variables that can then be included in linear regression or other models. This technique is called principal component regression (PCR) and it allows researchers to examine the effect of several correlated explanatory variables on a single response variable in cases where a high degree of correlation initially prevents them from being included in the same model. Principal component regression (PCR) is just one example of how principal components can be used in further analysis of data. When carrying out PCR, the variable of interest (response/dependent variable) is regressed against the principal components calculated using PCA, rather than against each individual explanatory variable from the original dataset. As there as many principal components created from PCA as there are variables in the dataset, we must select which principal components to include in PCR. This can be done by examining the amount of variation in the data explained by each principal component (see above).
Further reading
- James, G., Witten, D., Hastie, T. & Tibshirani, R. (2013) An Introduction to Statistical Learning with Applications in R. Chapter 6.3 (Dimension Reduction Methods), Chapter 10 (Unsupervised Learning).
- Jolliffe, I.T. & Cadima, J. (2016) Principal component analysis: a review and recent developments. Phil. Trans. R. Soc A 374..
- Johnstone, I.M. & Titterington, D.M. (2009) Statistical challenges of high-dimensional data. Phil. Trans. R. Soc A 367.
- PCA: A Practical Guide to Principal Component Analysis, Analytics Vidhya.
- A One-Stop Shop for Principal Component Analysis, Towards Data Science.
Key Points
A principal component analysis is a statistical approach used to reduce dimensionality in high-dimensional datasets (i.e. where $p$ is equal or greater than $n$).
PCA may be used to create a low-dimensional set of features from a larger set of variables. Examples of when a PCA may be useful include reducing high-dimensional datasets to fewer variables for use in a linear regression and for identifying groups with similar features.
PCA is a useful dimensionality reduction technique used in the analysis of complex biological datasets (e.g. high throughput data or genetics data).
The first principal component represents the dimension along which there is maximum variation in the data. Subsequent principal components represent dimensions with progressively less variation.
Scree plots and biplots may be used to show: 1. how much variation in the data is explained by each principal component and 2. how data points cluster according to principal component scores and which variables are associated with these scores.