Hierarchical clustering

Last updated on 2025-02-03 | Edit this page

Overview

Questions

What is hierarchical clustering and how does it differ from other clustering methods?
How do we carry out hierarchical clustering in R?
What distance matrix and linkage methods should we use?
How can we validate identified clusters?

Objectives

Understand when to use hierarchical clustering on high-dimensional data.
Perform hierarchical clustering on high-dimensional data and evaluate dendrograms.
Understand and explore different distance matrix and linkage methods.
Use the Dunn index to validate clustering methods.

Why use hierarchical clustering on high-dimensional data?

When analysing high-dimensional data in the life sciences, it is often useful to identify groups of similar data points to understand more about the relationships within the dataset. General clustering algorithms group similar data points (or observations) into groups (or clusters). This results in a set of clusters, where each cluster is distinct, and the data points within each cluster have similar characteristics. The clustering algorithm works by iteratively grouping data points so that different clusters may exist at different stages of the algorithm’s progression.

Here, we describe hierarchical clustering. Unlike K-means clustering, hierarchical clustering does not require the number of clusters \(k\) to be specified by the user before the analysis is carried out.

Hierarchical clustering also provides an attractive dendrogram, a tree-like diagram showing the degree of similarity between clusters. The dendrogram is a key feature of hierarchical clustering. This tree-shaped graph allows the similarity between data points in a dataset to be visualised and the arrangement of clusters produced by the analysis to be illustrated. Dendrograms are created using a distance (or dissimilarity) that quantify how different are pairs of observations, and a clustering algorithm to fuse groups of similar data points together.

In this episode we will explore hierarchical clustering for identifying clusters in high-dimensional data. We will use agglomerative hierarchical clustering (see box) in this episode.

Agglomerative and Divisive hierarchical clustering

There are two main methods of carrying out hierarchical clustering: agglomerative clustering and divisive clustering. The former is a ‘bottom-up’ approach to clustering whereby the clustering approach begins with each data point (or observation) being regarded as being in its own separate cluster. Pairs of data points are merged as we move up the tree. Divisive clustering is a ‘top-down’ approach in which all data points start in a single cluster and an algorithm is used to split groups of data points from this main group.

The agglomerative hierarchical clustering algorithm

To start with, we measure distance (or dissimilarity) between pairs of observations. Initially, and at the bottom of the dendrogram, each observation is considered to be in its own individual cluster. We start the clustering procedure by fusing the two observations that are most similar according to a distance matrix. Next, the next-most similar observations are fused so that the total number of clusters is number of observations minus 2 (see panel below). Groups of observations may then be merged into a larger cluster (see next panel below, green box). This process continues until all the observations are included in a single cluster.

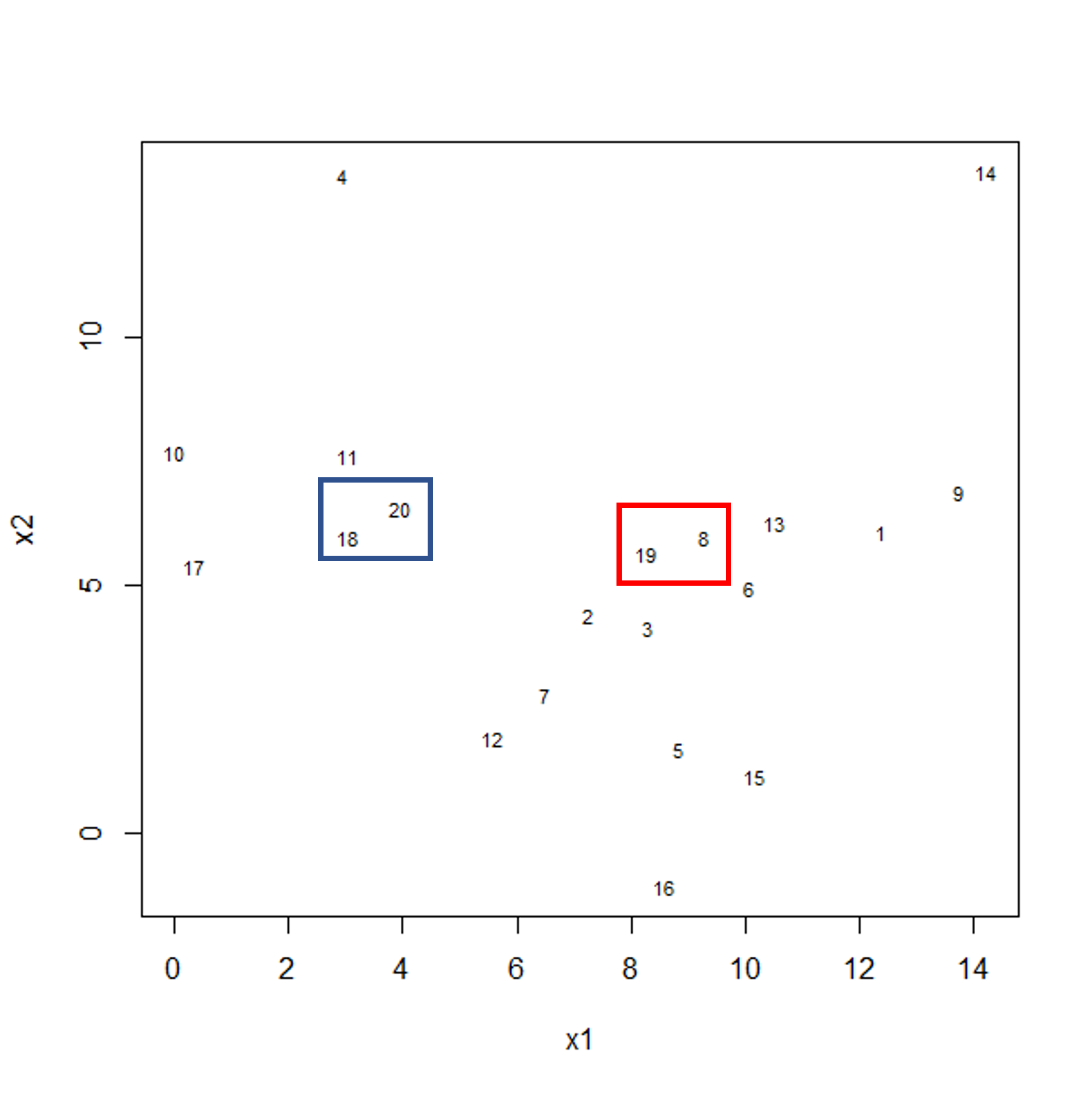
Scatter plot of observations x2 versus x1. Two clusters of pairs of observations are shown by blue and red boxes, each grouping two observations that are close in their x and y distance. — Example data showing two clusters of observation pairs.

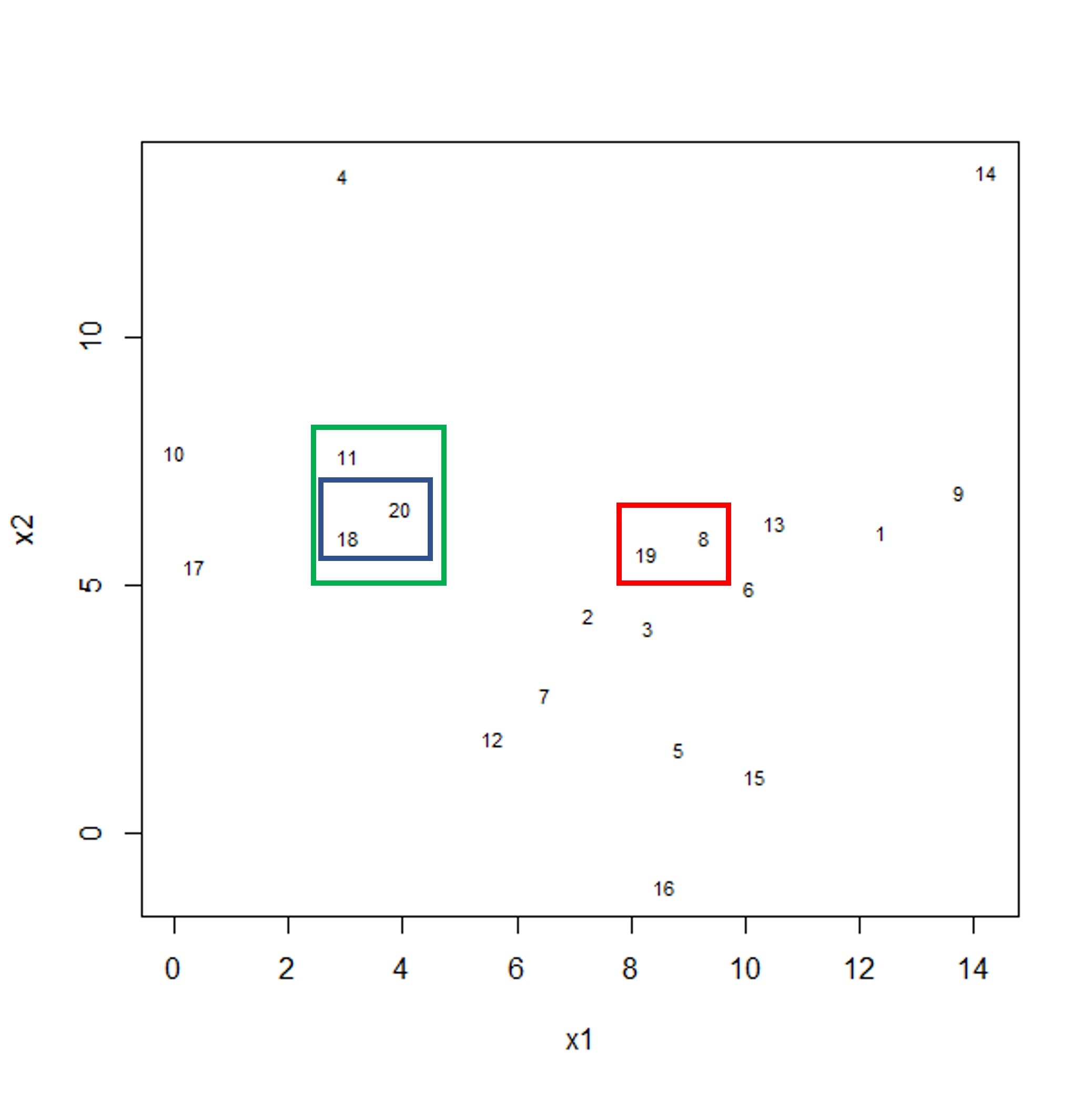
Scatter plot of observations x2 versus x1. Three boxes are shown this time. Blue and red boxes contain two observations each. The two boxes contain points that are relatively far apart. A third green box is shown encompassing the blue box and an additional data point. — Example data showing fusing of one observation into larger cluster.

A motivating example

To motivate this lesson, let’s first look at an example where hierarchical clustering is really useful, and then we can understand how to apply it in more detail. To do this, we’ll return to the large methylation dataset we worked with in the regression lessons. Let’s load and visually inspect the data:

R

methyl <- readRDS("data/methylation.rds")

# transpose this Bioconductor dataset to show features in columns
methyl_mat <- t(assay(methyl))

ERROR

Error in assay(methyl): could not find function "assay"

Looking at a heatmap of these data, we may spot some patterns – many columns appear to have a similar methylation levels across all rows. However, they are all quite jumbled at the moment, so it’s hard to tell how many line up exactly.

ERROR

Error in pheatmap(methyl_mat, legend_title = "Methylation level", cluster_rows = FALSE, : could not find function "pheatmap"

Looking at a heatmap of these data, we may spot some patterns – looking at the vertical stripes, many columns appear to have a similar methylation levels across all rows. However, they are all quite jumbled at the moment, so it’s hard to tell how many line up exactly. In addition, it is challenging to tell how many groups containing similar methylation levels we may have or what the similarities and differences are between groups.

We can order these data to make the patterns more clear using hierarchical clustering. To do this, we can change the arguments we pass to pheatmap() from the pheatmap package. pheatmap() groups features based on dissimilarity (here, Euclidean distance) and orders rows and columns to show clustering of features and observations.

R

pheatmap(methyl_mat,
         legend_title = "Methylation level",
         cluster_rows = TRUE, 
         cluster_cols = TRUE,
         show_rownames = FALSE, 
         show_colnames = FALSE,
         main = "Methylation Sites vs Individuals",
         annotation_legend = TRUE)

ERROR

Error in pheatmap(methyl_mat, legend_title = "Methylation level", cluster_rows = TRUE, : could not find function "pheatmap"

We can see that clustering the features (CpG sites) results in an overall gradient of high to low methylation levels from left to right. Maybe more interesting is the fact that the rows (corresponding to individuals) are now grouped according to methylation patterns. For example, 12 samples seem to have lower methylation levels for a small subset of CpG sites in the middle, relative to all the other samples. It’s not clear without investigating further what the cause of this is – it could be a batch effect, or a known grouping (e.g., old vs young samples). However, clustering like this can be a useful part of exploratory analysis of data to build hypotheses.

Hierarchical clustering

Now, let’s cover the inner workings of hierarchical clustering in more detail. Hierarchical clustering is a type of clustering that also allows us to estimate the number of clusters. There are two things to consider before carrying out clustering:

how to define dissimilarity between observations using a distance matrix, and
how to define dissimilarity between clusters and when to fuse separate clusters.

Defining the dissimilarity between observations: creating the distance matrix

Agglomerative hierarchical clustering is performed in two steps: calculating the distance matrix (containing distances between pairs of observations) and iteratively grouping observations into clusters using this matrix.

There are different ways to specify a distance matrix for clustering:

Specify distance as a pre-defined option using the method argument in dist(). Methods include euclidean (default), maximum and manhattan.
Create a self-defined function which calculates distance from a matrix or from two vectors. The function should only contain one argument.

Of pre-defined methods of calculating the distance matrix, Euclidean is one of the most commonly used. This method calculates the shortest straight-line distances between pairs of observations.

Another option is to use a correlation matrix as the input matrix to the clustering algorithm. The type of distance matrix used in hierarchical clustering can have a big effect on the resulting tree. The decision of which distance matrix to use before carrying out hierarchical clustering depends on the type of data and question to be addressed.

Defining the dissimilarity between clusters: Linkage methods

The second step in performing hierarchical clustering after defining the distance matrix (or another function defining similarity between data points) is determining how to fuse different clusters.

Linkage is used to define dissimilarity between groups of observations (or clusters) and is used to create the hierarchical structure in the dendrogram. Different linkage methods of creating a dendrogram are discussed below.

hclust() supports various linkage methods (e.g complete, single, ward D, ward D2, average, median) and these are also supported within the pheatmap() function. The method used to perform hierarchical clustering in pheatmap() can be specified by the argument clustering_method. Each linkage method uses a slightly different algorithm to calculate how clusters are fused together and therefore different clustering decisions are made depending on the linkage method used.

Complete linkage (the default in hclust()) works by computing all pairwise dissimilarities between data points in different clusters. For each pair of two clusters, it sets their dissimilarity to the maximum dissimilarity value observed between any of these clusters’ constituent points. The two clusters with smallest dissimilarity value are then fused.

Computing a dendrogram

Dendrograms are useful tools that plot the grouping of points and clusters into bigger clusters. We can create and plot dendrograms in R using hclust() which takes a distance matrix as input and creates a tree using hierarchical clustering. Here we create some example data to carry out hierarchical clustering.

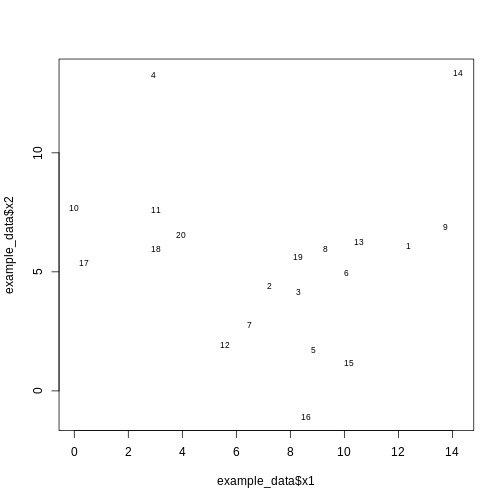
Let’s generate 20 data points in 2D space. Each point is generated to belong to one of three classes/groups. Suppose we did not know which class data points belonged to and we want to identify these via cluster analysis. Let’s first generate and plot our data:

R

#First, create some example data with two variables x1 and x2
set.seed(450)
example_data <- data.frame(
    x1 = rnorm(20, 8, 4.5),
    x2 = rnorm(20, 6, 3.4)
)

#plot the data and name data points by row numbers
plot(example_data$x1, example_data$x2, type = "n")
text(
    example_data$x1,
    example_data$x2,
    labels = rownames(example_data),
    cex = 0.7
)

A scatter plot of randomly-generated data x2 versus x1. The points appear fairly randomly scattered, arguably centered towards the bottom of the plot. — Scatter plot of randomly-generated data x2 versus x1.

R

## calculate distance matrix using euclidean distance
dist_m <- dist(example_data, method = "euclidean")

Hierarchical clustering carried out on the data can be used to produce a dendrogram showing how the data is partitioned into clusters. But how do we interpret this dendrogram? Let’s explore this using our example data in a Challenge.

Challenge 1

Use hclust() to implement hierarchical clustering using the distance matrix dist_m and the complete linkage method and plot the results as a dendrogram using plot(). Why is hierarchical clustering and the resulting dendrogram useful for performing clustering this case?

Solution:

R

clust <- hclust(dist_m, method = "complete")
plot(clust)

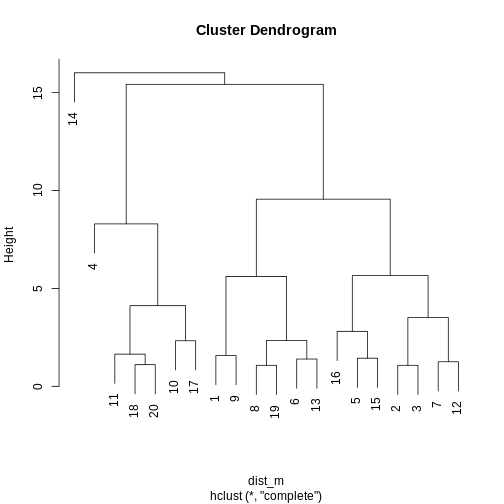
A line plot depicting a dendrogram --- a tree structure representing the hierarchical structure of the data. The data broadly fit into three clusters, with one sample (14) being quite dissimilar to all others, and the rest of the data comprising two other clusters (one larger than the other). — A dendrogram of the randomly-generated data.

Hierarchical clustering is particularly useful (compared to K-means) when we do not know the number of clusters before we perform clustering. It is useful in this case since we have assumed we do not already know what a suitable number of clusters may be.

A dendrogram, such as the one generated in Challenge 1, shows similarities/differences in distances between data points. Each vertical line at the bottom of the dendrogram (‘leaf’) represents one of the 20 data points. These leaves fuse into fewer vertical lines (‘branches’) as the height increases. Observations that are similar fuse into the same branches. The height at which any two data points fuse indicates how different these two points are. Points that fuse at the top of the tree are very different from each other compared with two points that fuse at the bottom of the tree, which are quite similar. You can see this by comparing the position of similar/dissimilar points according to the scatterplot with their position on the tree.

Identifying the number of clusters

To identify the number of clusters, we can make a horizontal cut through the dendrogram at a user-defined height. The sets of observations beneath this cut and single points representing clusters above can be thought of as distinct clusters. Equivalently, we can count the vertical lines we encounter crossing the horizontal cut and the number of single points above the cut. For example, a cut at height 10 produces 3 clusters for the dendrogram in Challenge 1, while a cut at height 4 produces 8 clusters.

Dendrogram visualisation

We can first visualise cluster membership by highlight branches in dendrograms. In this example, we calculate a distance matrix between samples in the methyl_mat dataset. We then draw boxes round clusters obtained with cutree().

R

## create a distance matrix using euclidean distance
distmat <- dist(methyl_mat)

ERROR

Error: object 'methyl_mat' not found

R

## hierarchical clustering using complete method
clust <- hclust(distmat)

ERROR

Error: object 'distmat' not found

R

## plot resulting dendrogram
plot(clust)

## draw border around three clusters
rect.hclust(clust, k = 3, border = 2:6) #border argument specifies the colours
## draw border around two clusters
rect.hclust(clust, k = 2, border = 2:6)

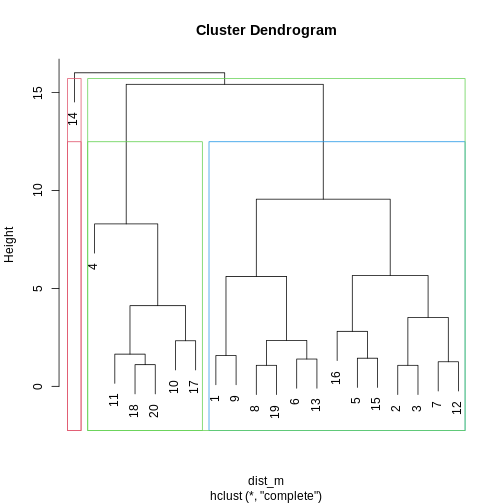
A dendrogram for the methyl_mat data with boxes overlaid on clusters. There are 5 boxes in total, each indicating separate clusters. — Dendrogram with boxes around clusters.

We can also colour clusters downstream of a specified cut using color_branches() from the dendextend package.

R

## cut tree at height = 4
cut <- cutree(clust, h = 50)

library("dendextend")

OUTPUT


---------------------
Welcome to dendextend version 1.19.0
Type citation('dendextend') for how to cite the package.

Type browseVignettes(package = 'dendextend') for the package vignette.
The github page is: https://github.com/talgalili/dendextend/

Suggestions and bug-reports can be submitted at: https://github.com/talgalili/dendextend/issues
You may ask questions at stackoverflow, use the r and dendextend tags:
	 https://stackoverflow.com/questions/tagged/dendextend

	To suppress this message use:  suppressPackageStartupMessages(library(dendextend))
---------------------

OUTPUT


Attaching package: 'dendextend'

OUTPUT

The following object is masked from 'package:stats':

    cutree

R

avg_dend_obj <- as.dendrogram(clust)      
## colour branches of dendrogram depending on clusters
plot(color_branches(avg_dend_obj, h = 50))

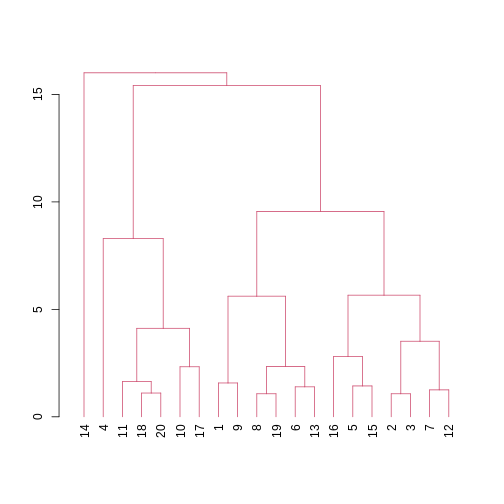
A dendrogram with the different clusters in 4 different colours. — Dendrogram with coloured branches delineating different clusters.

Numerical visualisation

In addition to visualising clusters directly on the dendrogram, we can cut the dendrogram to determine number of clusters at different heights using cutree(). This function cuts a dendrogram into several groups (or clusters) where the number of desired groups is controlled by the user, by defining either k (number of groups) or h (height at which tree is cut). The function outputs the cluster labels of each data point in order.

R

## k is a user defined parameter determining
## the desired number of clusters at which to cut the treee
as.numeric(cutree(clust, k = 9))

OUTPUT

 [1] 1 2 2 3 4 5 6 5 1 7 8 6 5 9 4 4 7 8 5 8

R

## h is a user defined parameter determining
## the numeric height at which to cut the tree
as.numeric(cutree(clust, h = 36))

OUTPUT

 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

R

## both give same results 

four_cut <- cutree(clust, h = 50)

## we can produce the cluster each observation belongs to
## using the mutate and count functions
library(dplyr)

OUTPUT


Attaching package: 'dplyr'

OUTPUT

The following objects are masked from 'package:stats':

    filter, lag

OUTPUT

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

R

example_cl <- mutate(data.frame(methyl_mat), cluster = four_cut)

ERROR

Error: object 'methyl_mat' not found

R

count(example_cl, cluster)

ERROR

Error: object 'example_cl' not found

R

#plot cluster each point belongs to on original scatterplot
library(ggplot2)
ggplot(example_cl, aes(x = cg01644850, y = cg01656216, color = factor(cluster))) + geom_point()

ERROR

Error: object 'example_cl' not found

Note that this cut produces 1 clusters (zero before the cut and another four downstream of the cut).

Challenge 2:

Identify the value of k in cutree() that gives the same output as h = 36

Solution:

R

plot(clust)
## create horizontal line at height = 45
abline(h = 45, lty = 2)

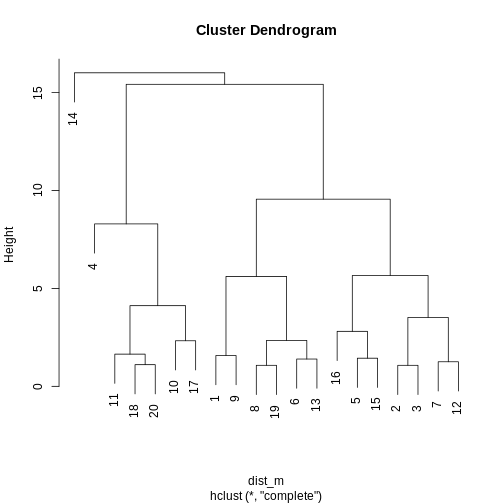
R

cutree(clust, h = 45)

OUTPUT

 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

R

cutree(clust, k = 5)

OUTPUT

 [1] 1 2 2 3 2 1 2 1 1 4 4 2 1 5 2 2 4 4 1 4

R

five_cut <- cutree(clust, h = 45)

library(dplyr)
example_cl <- mutate(data.frame(methyl_mat), cluster = five_cut)

ERROR

Error: object 'methyl_mat' not found

R

count(example_cl, cluster)

ERROR

Error: object 'example_cl' not found

R

library(ggplot2)
ggplot(example_cl, aes(x=cg01644850, y = cg01656216, color = factor(cluster))) + geom_point()

ERROR

Error: object 'example_cl' not found

Five clusters (k = 5) gives similar results to h = 45. You can plot a horizontal line on the dendrogram at h = 45 to help identify corresponding value of k.

The effect of different linkage methods

Now let us look into changing the default behaviour of hclust(). First, we’ll load a synthetic dataset, comprised of two variables representing two crescent-shaped point clouds:

R

cres <- readRDS("data/cres.rds")
plot(cres)

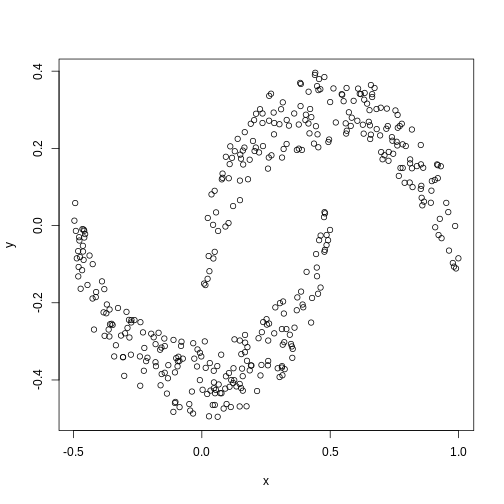
A scatter plot of data simulated to form two crescent shapes. The crescents are horizontally orientated with a a rough line of vertical symmetry. — Scatter plot of data simulated according to two crescent-shaped point clouds.

We might expect that the crescents are resolved into separate clusters. But if we run hierarchical clustering with the default arguments, we get this:

R

cresClass <- cutree(hclust(dist(cres)), k=2) # save partition for colouring
plot(cres, col=cresClass) # colour scatterplot by partition

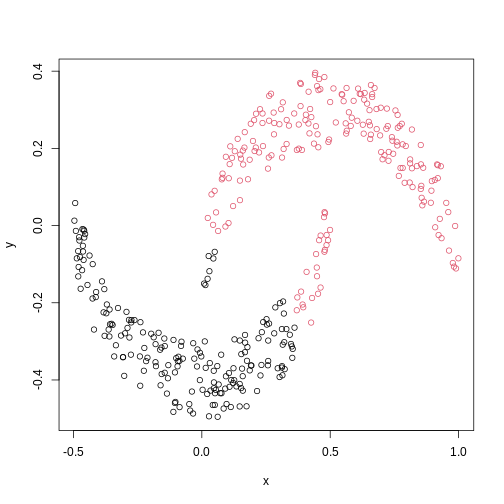
A scatter plot of the crescent-shaped simulated data calculated using Euclidean distance. The points are coloured in black or red according to their membership to 2 clusters. The points in the tails of each crescent have inherited the colour of the opposite crescent. — Scatter plot of crescent-shaped simulated data, coloured according to clusters calculated using Euclidean distance.

Challenge 3

Carry out hierarchical clustering on the cres data that we generated above. Try out different linkage methods and use cutree() to split each resulting dendrogram into two clusters. Plot the results colouring the dots according to their inferred cluster identity.

Which method(s) give you the expected clustering outcome?

Hint: Check ?hclust to see the possible values of the argument method (the linkage method used).

Solution:

R

#?hclust
# "complete", "single", "ward.D", "ward.D2", "average", "mcquitty", "median" or "centroid"
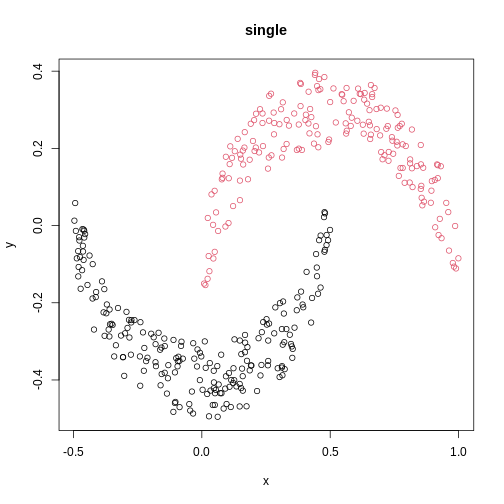
cresClassSingle <- cutree(hclust(dist(cres),method = "single"), k=2)
plot(cres, col=cresClassSingle, main="single")

A scatter plot of synthetic data, comprising two variables, with points forming two crescent-shaped clusters. Points are coloured based on hierarchical clustering with single linkage, with two clusters, corresponding to the two crescent-shaped clouds. — A scatter plot of synthetic data coloured by cluster.

R

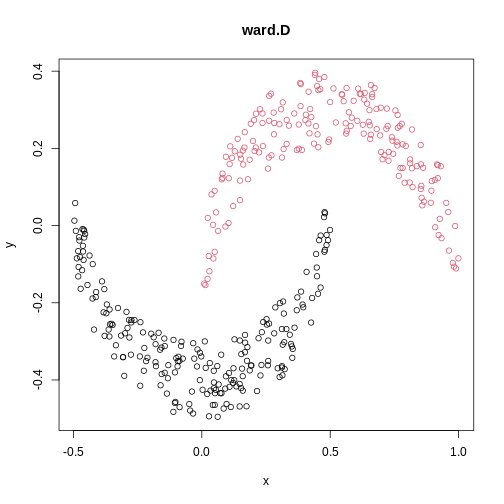
cresClassWard.D <- cutree(hclust(dist(cres), method="ward.D"), k=2)
plot(cres, col=cresClassWard.D, main="ward.D")

R

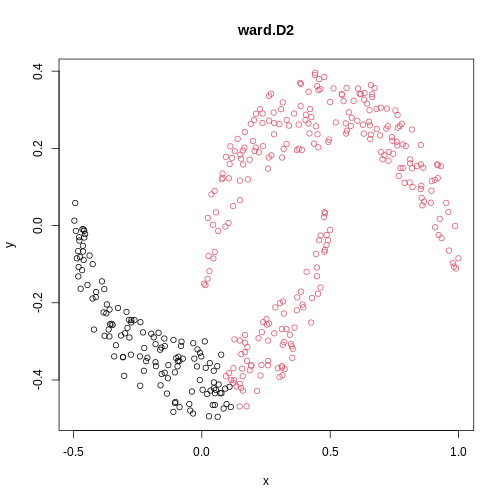
cresClassWard.D2 <- cutree(hclust(dist(cres), method="ward.D2"), k=2)
plot(cres, col=cresClassWard.D2, main="ward.D2")

R

cresClassAverage <- cutree(hclust(dist(cres), method="average"), k=2)
plot(cres, col=cresClassAverage, main="average")

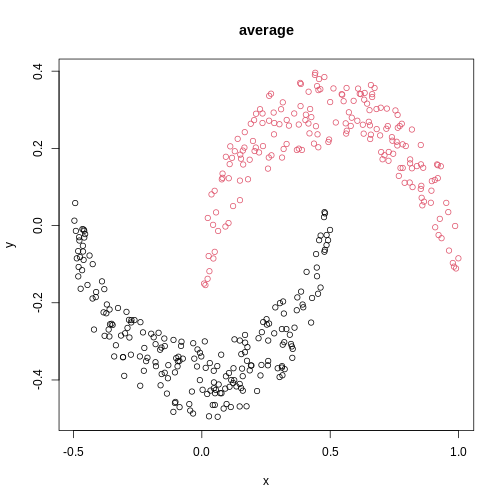
R

cresClassMcquitty <- cutree(hclust(dist(cres), method="mcquitty"), k=2)
plot(cres, col=cresClassMcquitty, main="mcquitty")

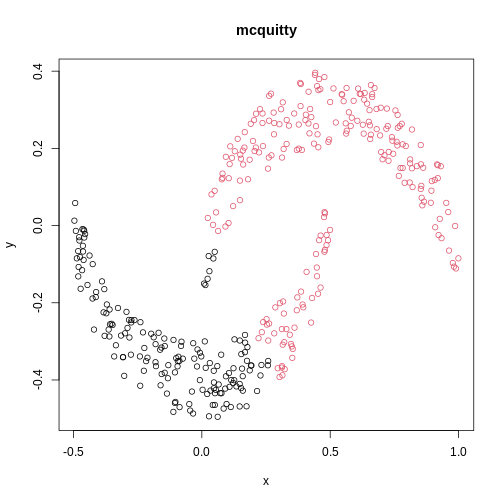
R

cresClassMedian<- cutree(hclust(dist(cres), method="median"), k=2) 
plot(cres, col=cresClassMedian, main="median")

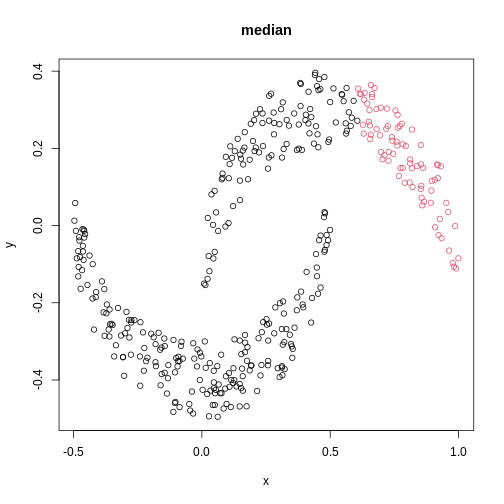
R

cresClassCentroid<- cutree(hclust(dist(cres), method="centroid"), k=2)
plot(cres, col=cresClassCentroid, main="centroid")

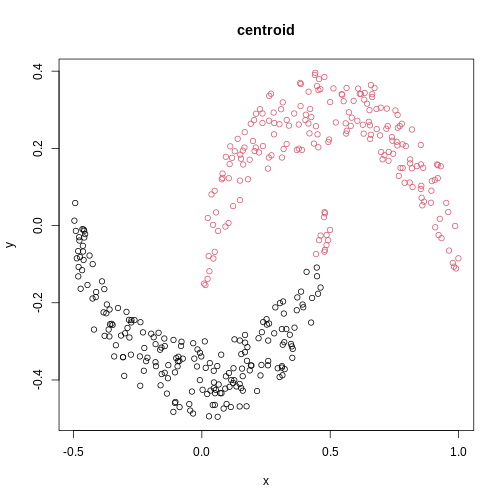
The linkage methods single, ward.D, and average resolve each crescent as a separate cluster.

The help page of hclust() gives some intuition on linkage methods. It describes complete (the default) and single as opposite ends of a spectrum with all other methods in between. When using complete linkage, the distance between two clusters is assumed to be the distance between both clusters’ most distant points. This opposite it true for single linkage, where the minimum distance between any two points, one from each of two clusters is used. Single linkage is described as friends-of-friends appporach - and really, it groups all close-together points into the same cluster (thus resolving one cluster per crescent). Complete linkage on the other hand recognises that some points a the tip of a crescent are much closer to points in the other crescent and so it splits both crescents.

Using different distance methods

So far, we’ve been using Euclidean distance to define the dissimilarity or distance between observations. However, this isn’t always the best metric for how dissimilar the observations are. Let’s make an example to demonstrate. Here, we’re creating two samples each with ten observations of random noise:

R

set.seed(20)
cor_example <- data.frame(
  sample_a = rnorm(10),
  sample_b = rnorm(10)
)
rownames(cor_example) <- paste(
  "Feature", 1:nrow(cor_example)
)

Now, let’s create a new sample that has exactly the same pattern across all our features as sample_a, just offset by 5:

R

cor_example$sample_c <- cor_example$sample_a + 5

You can see that this is a lot like the assay() of our methylation object from earlier, where columns are observations or samples, and rows are features:

R

head(cor_example)

OUTPUT

            sample_a    sample_b sample_c
Feature 1  1.1626853 -0.02013537 6.162685
Feature 2 -0.5859245 -0.15038222 4.414076
Feature 3  1.7854650 -0.62812676 6.785465
Feature 4 -1.3325937  1.32322085 3.667406
Feature 5 -0.4465668 -1.52135057 4.553433
Feature 6  0.5696061 -0.43742787 5.569606

If we plot a heatmap of this, we can see that sample_a and sample_b are grouped together because they have a small distance from each other, despite being quite different in their pattern across the different features. In contrast, sample_a and sample_c are very distant, despite having exactly the same pattern across the different features.

R

pheatmap(as.matrix(cor_example))

ERROR

Error in pheatmap(as.matrix(cor_example)): could not find function "pheatmap"

We can see that more clearly if we do a line plot:

R

## create a blank plot (type = "n" means don't draw anything)
## with an x range to hold the number of features we have.
## the range of y needs to be enough to show all the values for every feature
plot(
  1:nrow(cor_example),
  rep(range(cor_example), 5),
  type = "n", 
  xlab = "Feature number",
  ylab = "Value"
)
## draw a red line for sample_a
lines(cor_example$sample_a, col = "firebrick")
## draw a blue line for sample_b
lines(cor_example$sample_b, col = "dodgerblue")
## draw a green line for sample_c
lines(cor_example$sample_c, col = "forestgreen")

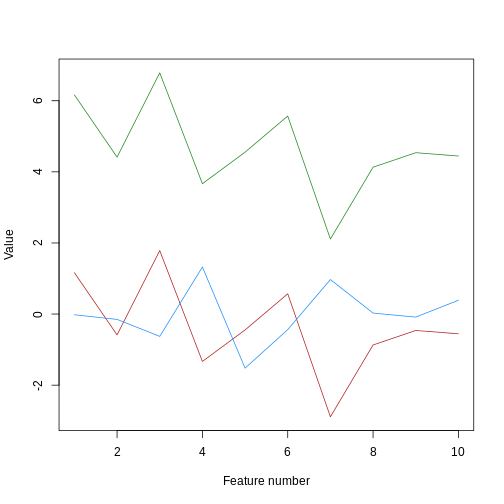
A line plot of simulated value versus observation number, coloured by sample. Samples a and b are concentrated at the bottom of the plot, while sample c is concentrated at the top of the plot. Samples a and c have exactly the same vertical pattern. — Line plot of simulated value versus observation number, coloured by sample.

We can see that sample_a and sample_c have exactly the same pattern across all of the different features. However, due to the overall difference between the values, they have a high distance to each other. We can see that if we cluster and plot the data ourselves using Euclidean distance:

R

clust_dist <- hclust(dist(t(cor_example)))
plot(clust_dist)

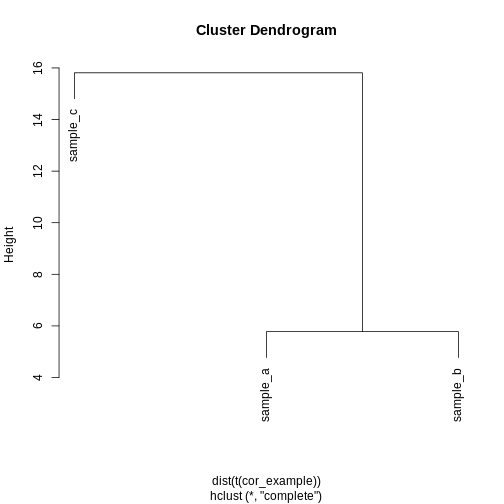
A dendrogram of the example simulated data clustered according to Euclidean distance. The dendrogram shows that sample c definitively forms its own cluster for any cut height and samples a and b merge into a cluster at a height of around 6. — Dendrogram of the example simulated data clustered according to Euclidean distance.

In some cases, we might want to ensure that samples that have similar patterns, whether that be of gene expression, or DNA methylation, have small distances to each other. Correlation is a measure of this kind of similarity in pattern. However, high correlations indicate similarity, while for a distance measure we know that high distances indicate dissimilarity. Therefore, if we wanted to cluster observations based on the correlation, or the similarity of patterns, we can use 1 - cor(x) as the distance metric. The input to hclust() must be a dist object, so we also need to call as.dist() on it before passing it in.

R

cor_as_dist <- as.dist(1 - cor(cor_example))
clust_cor <- hclust(cor_as_dist)
plot(clust_cor)

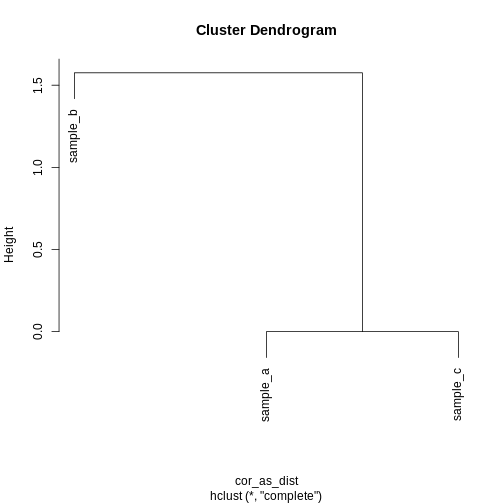
A dendrogram of the example simulated data clustered according to correlation. The dendrogram shows that sample b definitively forms its own cluster and samples a and c form definitively form their own cluster for any cut height. — Dendrogram of the example simulated data clustered according to correlation.

Now, sample_a and sample_c that have identical patterns across the features are grouped together, while sample_b is seen as distant because it has a different pattern, even though its values are closer to sample_a. Using your own distance function is often useful, especially if you have missing or unusual data. It’s often possible to use correlation and other custom dissimilarity measures in functions that perform hierarchical clustering, such as pheatmap() and stats::heatmap():

R

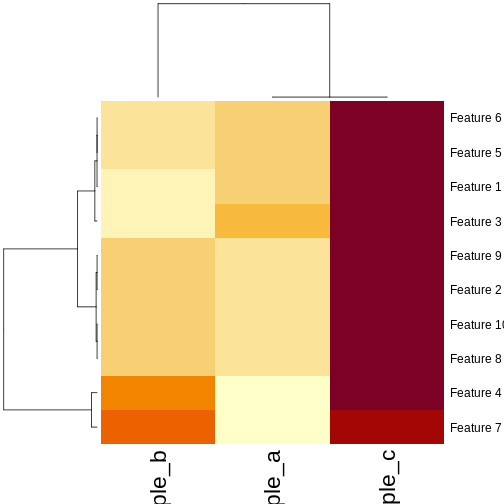
## pheatmap allows you to select correlation directly
pheatmap(as.matrix(cor_example), clustering_distance_cols = "correlation")

ERROR

Error in pheatmap(as.matrix(cor_example), clustering_distance_cols = "correlation"): could not find function "pheatmap"

R

## Using the built-in stats::heatmap 
heatmap(
  as.matrix(cor_example),
  distfun = function(x) as.dist(1 - cor(t(x)))
)

Heatmaps of features versus samples, coloured by simulated value. The columns (samples) are clustered according to the correlation. Samples a and b have mostly low values, delineated by blue in the first plot and yellow in the second plot. Sample c has mostly high values, delineated by red in the first plot and brown in the second plot. Samples A and C form a cluster separate from sample B in the column dendrogram. — Heatmaps of features versus samples clustered in the samples according to correlation.

Validating clusters

Now that we know how to carry out hierarchical clustering, how do we know how many clusters are optimal for the dataset?

Hierarchical clustering carried out on any dataset will produce clusters, even when there are no ‘real’ clusters in the data! We need to be able to determine whether identified clusters represent true groups in the data, or whether clusters have been identified just due to chance. In the last episode, we have introduced silhouette scores as a measure of cluster compactness and bootstrapping to assess cluster robustness. Such tests can be used to compare different clustering algorithms, for example, those fitted using different linkage methods.

Here, we introduce the Dunn index, which is a measure of cluster compactness. The Dunn index is the ratio of the smallest distance between any two clusters and to the largest intra-cluster distance found within any cluster. This can be seen as a family of indices which differ depending on the method used to compute distances. The Dunn index is a metric that penalises clusters that have larger intra-cluster variance and smaller inter-cluster variance. The higher the Dunn index, the better defined the clusters.

Let’s calculate the Dunn index for clustering carried out on the methyl_mat dataset using the clValid package.

R

## calculate dunn index
## (ratio of the smallest distance between obs not in the same cluster
## to the largest intra-cluster distance)
library("clValid")

OUTPUT

Loading required package: cluster

R

## calculate euclidean distance between points 
distmat <- dist(methyl_mat)

ERROR

Error: object 'methyl_mat' not found

R

clust <- hclust(distmat, method = "complete")

ERROR

Error: object 'distmat' not found

R

plot(clust)

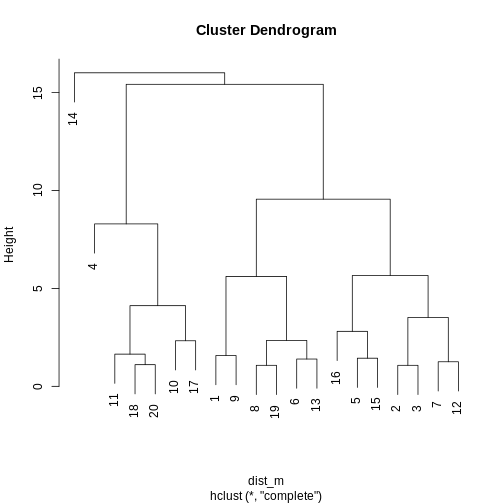
A dendrogram for clustering of methylation data. Identical to that in the section Highlighting dendrogram branches, without the colour overlay to show clusters. — Dendrogram for clustering of methylation data.

R

cut <- cutree(clust, h = 50)

## retrieve Dunn's index for given matrix and clusters
dunn(distance = distmat, cut)

ERROR

Error: object 'distmat' not found

The value of the Dunn index has no meaning in itself, but is used to compare between sets of clusters with larger values being preferred.

Challenge 4

Examine how changing the h or k arguments in cutree() affects the value of the Dunn index.

Solution:

R

library("clValid")

distmat <- dist(methyl_mat)

ERROR

Error: object 'methyl_mat' not found

R

clust <- hclust(distmat, method = "complete")

ERROR

Error: object 'distmat' not found

R

#Varying h
## Obtaining the clusters
cut_h_20 <- cutree(clust, h = 20)
cut_h_30 <- cutree(clust, h = 30)

## How many clusters?
length(table(cut_h_20))

OUTPUT

[1] 1

R

length(table(cut_h_30))

OUTPUT

[1] 1

R

dunn(distance = distmat, cut_h_20)

ERROR

Error: object 'distmat' not found

R

dunn(distance = distmat, cut_h_30)

ERROR

Error: object 'distmat' not found

R

#Varying k
## Obtaining the clusters
cut_k_10 <- cutree(clust, k = 10)
cut_k_5 <- cutree(clust, k = 5)

## How many clusters?
length(table(cut_k_5))

OUTPUT

[1] 5

R

length(table(cut_k_10))

OUTPUT

[1] 10

R

dunn(distance = distmat, cut_k_5)

ERROR

Error: object 'distmat' not found

R

dunn(distance = distmat, cut_k_10)

ERROR

Error: object 'distmat' not found

The figures below show in a more systematic way how changing the values of k and h using cutree() affect the Dunn index.

R

h_seq <- 70:10
h_dunn <- sapply(h_seq, function(x) dunn(distance = distmat, cutree(clust, h = x)))

ERROR

Error in FUN(X[[i]], ...): object 'distmat' not found

R

k_seq <- seq(2, 10)
k_dunn <- sapply(k_seq, function(x) dunn(distance = distmat, cutree(clust, k = x)))

ERROR

Error in FUN(X[[i]], ...): object 'distmat' not found

R

plot(h_seq, h_dunn, xlab = "Height (h)", ylab = "Dunn index")

ERROR

Error in h(simpleError(msg, call)): error in evaluating the argument 'y' in selecting a method for function 'plot': object 'h_dunn' not found

R

grid()

ERROR

Error in int_abline(a = a, b = b, h = h, v = v, untf = untf, ...): plot.new has not been called yet

You can see that at low values of h, the Dunn index can be high. But this is not very useful - cutting the given tree at a low h value like 15 leads to allmost all observations ending up each in its own cluster. More relevant is the second maximum in the plot, around h=55. Looking at the dendrogram, this corresponds to k=4.

R

plot(k_seq, k_dunn, xlab = "Number of clusters (k)", ylab = "Dunn index")

ERROR

Error in h(simpleError(msg, call)): error in evaluating the argument 'y' in selecting a method for function 'plot': object 'k_dunn' not found

R

grid()

ERROR

Error in int_abline(a = a, b = b, h = h, v = v, untf = untf, ...): plot.new has not been called yet

For the given range of k values explored, we obtain the highest Dunn index with k=4. This is in agreement with the previous plot.

There have been criticisms of the use of the Dunn index in validating clustering results, due to its high sensitivity to noise in the dataset. An alternative is to use silhouette scores (see the k-means clustering episode).

As we said before (see previous episode), clustering is a non-trivial task. It is important to think about the nature of your data and your expectations rather than blindly using a some algorithm for clustering or cluster validation.