Extra exploration of design matrices
Last updated on 2024-12-03 | Edit this page
Overview
Questions
- How can one translate biological questions and comparisons to statistical terms suitable for use with RNA-seq analysis packages?
Objectives
- Explain the formula notation and design matrices.
- Explore different designs and learn how to interpret coefficients.
Loading required packages and reading data
We start by loading a few packages that will be needed in this episode. In particular, the ExploreModelMatrix package provides resources for exploring design matrices in a graphical fashion, for easier interpretation.
R
suppressPackageStartupMessages({
library(SummarizedExperiment)
library(ExploreModelMatrix)
library(dplyr)
library(DESeq2)
})
Next, we read the metadata table for our data set. Because we want to explore many different design matrices, we will read in the 4th file we downloaded but haven’t used yet: that for both Cerebellum and Spinal Cord samples (45 samples total). As seen in previous episodes, the metadata contains information about the age, sex, infection status, time of measurement and tissue of the collected samples. Note that Day0 always corresponds to non-infected samples, and that infected samples are collected on days 4 and 8. Moreover, all mice have the same age (8 weeks). Hence, in the first part of this episode we consider only the sex, tissue and time variables further.
R
meta <- read.csv("data/GSE96870_coldata_all.csv", row.names = 1)
meta
OUTPUT
title geo_accession organism age sex
GSM2545336 CNS_RNA-seq_10C GSM2545336 Mus musculus 8 weeks Female
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545339 CNS_RNA-seq_13C GSM2545339 Mus musculus 8 weeks Female
GSM2545340 CNS_RNA-seq_14C GSM2545340 Mus musculus 8 weeks Male
GSM2545341 CNS_RNA-seq_17C GSM2545341 Mus musculus 8 weeks Male
GSM2545342 CNS_RNA-seq_1C GSM2545342 Mus musculus 8 weeks Female
GSM2545343 CNS_RNA-seq_20C GSM2545343 Mus musculus 8 weeks Male
GSM2545344 CNS_RNA-seq_21C GSM2545344 Mus musculus 8 weeks Female
GSM2545345 CNS_RNA-seq_22C GSM2545345 Mus musculus 8 weeks Male
GSM2545346 CNS_RNA-seq_25C GSM2545346 Mus musculus 8 weeks Male
GSM2545347 CNS_RNA-seq_26C GSM2545347 Mus musculus 8 weeks Male
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545349 CNS_RNA-seq_28C GSM2545349 Mus musculus 8 weeks Male
GSM2545350 CNS_RNA-seq_29C GSM2545350 Mus musculus 8 weeks Male
GSM2545351 CNS_RNA-seq_2C GSM2545351 Mus musculus 8 weeks Female
GSM2545352 CNS_RNA-seq_30C GSM2545352 Mus musculus 8 weeks Female
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545354 CNS_RNA-seq_4C GSM2545354 Mus musculus 8 weeks Male
GSM2545355 CNS_RNA-seq_571 GSM2545355 Mus musculus 8 weeks Male
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545359 CNS_RNA-seq_585 GSM2545359 Mus musculus 8 weeks Female
GSM2545360 CNS_RNA-seq_589 GSM2545360 Mus musculus 8 weeks Male
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545362 CNS_RNA-seq_5C GSM2545362 Mus musculus 8 weeks Female
GSM2545363 CNS_RNA-seq_6C GSM2545363 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
GSM2545368 CNS_RNA-seq_728 GSM2545368 Mus musculus 8 weeks Male
GSM2545369 CNS_RNA-seq_729 GSM2545369 Mus musculus 8 weeks Male
GSM2545370 CNS_RNA-seq_730 GSM2545370 Mus musculus 8 weeks Female
GSM2545371 CNS_RNA-seq_731 GSM2545371 Mus musculus 8 weeks Female
GSM2545372 CNS_RNA-seq_733 GSM2545372 Mus musculus 8 weeks Male
GSM2545373 CNS_RNA-seq_735 GSM2545373 Mus musculus 8 weeks Male
GSM2545374 CNS_RNA-seq_736 GSM2545374 Mus musculus 8 weeks Female
GSM2545375 CNS_RNA-seq_738 GSM2545375 Mus musculus 8 weeks Female
GSM2545376 CNS_RNA-seq_740 GSM2545376 Mus musculus 8 weeks Female
GSM2545377 CNS_RNA-seq_741 GSM2545377 Mus musculus 8 weeks Female
GSM2545378 CNS_RNA-seq_742 GSM2545378 Mus musculus 8 weeks Male
GSM2545379 CNS_RNA-seq_743 GSM2545379 Mus musculus 8 weeks Male
GSM2545380 CNS_RNA-seq_9C GSM2545380 Mus musculus 8 weeks Female
infection strain time tissue mouse
GSM2545336 InfluenzaA C57BL/6 Day8 Cerebellum 14
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10
GSM2545339 InfluenzaA C57BL/6 Day4 Cerebellum 15
GSM2545340 InfluenzaA C57BL/6 Day4 Cerebellum 18
GSM2545341 InfluenzaA C57BL/6 Day8 Cerebellum 6
GSM2545342 InfluenzaA C57BL/6 Day8 Cerebellum 5
GSM2545343 NonInfected C57BL/6 Day0 Cerebellum 11
GSM2545344 InfluenzaA C57BL/6 Day4 Cerebellum 22
GSM2545345 InfluenzaA C57BL/6 Day4 Cerebellum 13
GSM2545346 InfluenzaA C57BL/6 Day8 Cerebellum 23
GSM2545347 InfluenzaA C57BL/6 Day8 Cerebellum 24
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8
GSM2545349 NonInfected C57BL/6 Day0 Cerebellum 7
GSM2545350 InfluenzaA C57BL/6 Day4 Cerebellum 1
GSM2545351 InfluenzaA C57BL/6 Day8 Cerebellum 16
GSM2545352 InfluenzaA C57BL/6 Day4 Cerebellum 21
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4
GSM2545354 NonInfected C57BL/6 Day0 Cerebellum 2
GSM2545355 InfluenzaA C57BL/6 Day4 Spinalcord 1
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545359 InfluenzaA C57BL/6 Day8 Spinalcord 5
GSM2545360 InfluenzaA C57BL/6 Day8 Spinalcord 6
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7
GSM2545362 InfluenzaA C57BL/6 Day4 Cerebellum 20
GSM2545363 InfluenzaA C57BL/6 Day4 Cerebellum 12
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11
GSM2545368 InfluenzaA C57BL/6 Day4 Spinalcord 12
GSM2545369 InfluenzaA C57BL/6 Day4 Spinalcord 13
GSM2545370 InfluenzaA C57BL/6 Day8 Spinalcord 14
GSM2545371 InfluenzaA C57BL/6 Day4 Spinalcord 15
GSM2545372 InfluenzaA C57BL/6 Day8 Spinalcord 17
GSM2545373 InfluenzaA C57BL/6 Day4 Spinalcord 18
GSM2545374 InfluenzaA C57BL/6 Day8 Spinalcord 19
GSM2545375 InfluenzaA C57BL/6 Day4 Spinalcord 20
GSM2545376 InfluenzaA C57BL/6 Day4 Spinalcord 21
GSM2545377 InfluenzaA C57BL/6 Day4 Spinalcord 22
GSM2545378 InfluenzaA C57BL/6 Day8 Spinalcord 23
GSM2545379 InfluenzaA C57BL/6 Day8 Spinalcord 24
GSM2545380 InfluenzaA C57BL/6 Day8 Cerebellum 19R
table(meta$time, meta$infection)
OUTPUT
InfluenzaA NonInfected
Day0 0 15
Day4 16 0
Day8 14 0R
table(meta$age)
OUTPUT
8 weeks
45 We can start by visualizing the number of observations for each combination of the three predictor variables.
R
vd <- VisualizeDesign(sampleData = meta,
designFormula = ~ tissue + time + sex)
vd$cooccurrenceplots
OUTPUT
$`tissue = Cerebellum`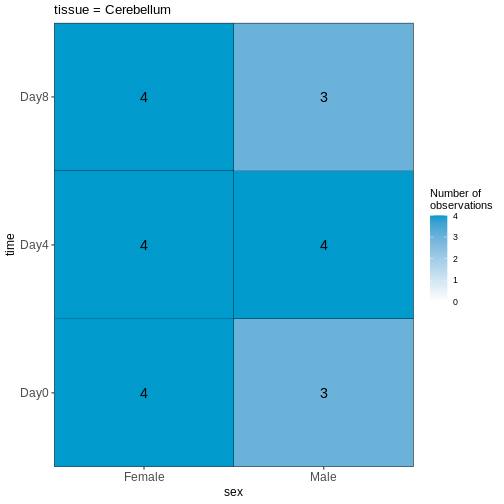
OUTPUT
$`tissue = Spinalcord`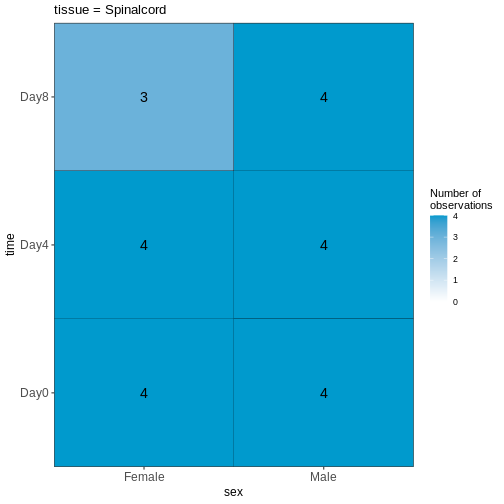
Challenge
Based on this visualization, would you say that the data set is balanced, or are there combinations of predictor variables that are severely over- or underrepresented?
Compare males and females, non-infected spinal cord
Next, we will set up our first design matrix. Here, we will focus on
the uninfected (Day0) spinal cord samples, and our aim is to compare the
male and female mice. Thus, we first subset the metadata to only the
samples of interest, and next set up and visualize the design matrix
with a single predictor variable (sex). By defining the design formula
as ~ sex, we tell R to include an intercept in the design.
This intercept will represent the ‘baseline’ level of the predictor
variable, which in this case is selected to be the Female mice. If not
explicitly specified, R will order the values of the predictor in
alphabetical order and select the first one as the reference or baseline
level.
R
## Subset metadata
meta_noninf_spc <- meta %>% filter(time == "Day0" &
tissue == "Spinalcord")
meta_noninf_spc
OUTPUT
title geo_accession organism age sex
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
infection strain time tissue mouse
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11R
## Use ExploreModelMatrix to create a design matrix and visualizations, given
## the desired design formula.
vd <- VisualizeDesign(sampleData = meta_noninf_spc,
designFormula = ~ sex)
vd$designmatrix
OUTPUT
(Intercept) sexMale
GSM2545356 1 1
GSM2545357 1 1
GSM2545358 1 0
GSM2545361 1 1
GSM2545364 1 0
GSM2545365 1 0
GSM2545366 1 0
GSM2545367 1 1R
vd$plotlist
OUTPUT
[[1]]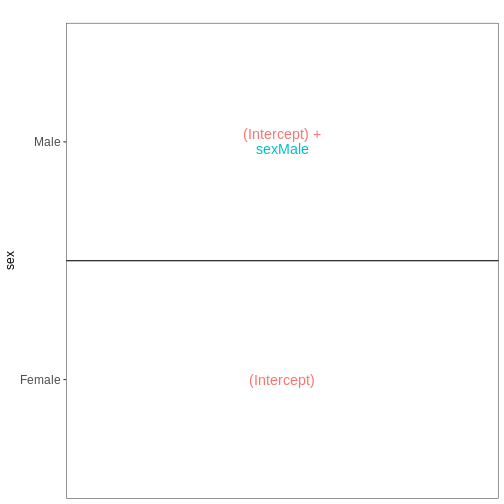
R
## Note that we can also generate the design matrix like this
model.matrix(~ sex, data = meta_noninf_spc)
OUTPUT
(Intercept) sexMale
GSM2545356 1 1
GSM2545357 1 1
GSM2545358 1 0
GSM2545361 1 1
GSM2545364 1 0
GSM2545365 1 0
GSM2545366 1 0
GSM2545367 1 1
attr(,"assign")
[1] 0 1
attr(,"contrasts")
attr(,"contrasts")$sex
[1] "contr.treatment"Challenge
With this design, what is the interpretation of the
sexMale coefficient?
Challenge
Set up the design formula to compare male and female spinal cord samples from Day0 as above, but instruct R to not include an intercept in the model. How does this change the interpretation of the coefficients? What contrast would have to be specified to compare the mean expression of a gene between male and female mice?
R
meta_noninf_spc <- meta %>% filter(time == "Day0" &
tissue == "Spinalcord")
meta_noninf_spc
OUTPUT
title geo_accession organism age sex
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
infection strain time tissue mouse
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11R
vd <- VisualizeDesign(sampleData = meta_noninf_spc,
designFormula = ~ 0 + sex)
vd$designmatrix
OUTPUT
sexFemale sexMale
GSM2545356 0 1
GSM2545357 0 1
GSM2545358 1 0
GSM2545361 0 1
GSM2545364 1 0
GSM2545365 1 0
GSM2545366 1 0
GSM2545367 0 1R
vd$plotlist
OUTPUT
[[1]]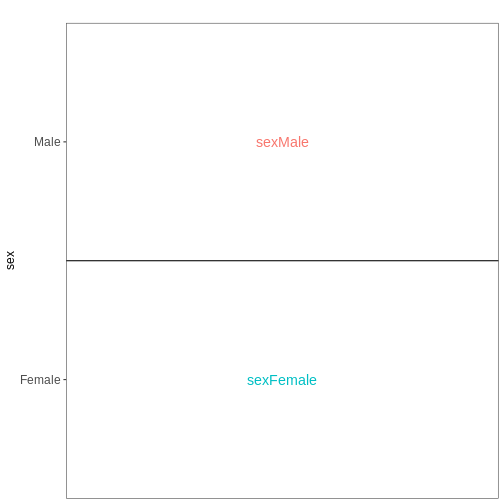
Challenge
Set up the design formula to compare the three time points (Day0,
Day4, Day8) in the male spinal cord samples, and visualize it using
ExploreModelMatrix.
R
meta_male_spc <- meta %>% filter(sex == "Male" & tissue == "Spinalcord")
meta_male_spc
OUTPUT
title geo_accession organism age sex infection
GSM2545355 CNS_RNA-seq_571 GSM2545355 Mus musculus 8 weeks Male InfluenzaA
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male NonInfected
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male NonInfected
GSM2545360 CNS_RNA-seq_589 GSM2545360 Mus musculus 8 weeks Male InfluenzaA
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male NonInfected
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male NonInfected
GSM2545368 CNS_RNA-seq_728 GSM2545368 Mus musculus 8 weeks Male InfluenzaA
GSM2545369 CNS_RNA-seq_729 GSM2545369 Mus musculus 8 weeks Male InfluenzaA
GSM2545372 CNS_RNA-seq_733 GSM2545372 Mus musculus 8 weeks Male InfluenzaA
GSM2545373 CNS_RNA-seq_735 GSM2545373 Mus musculus 8 weeks Male InfluenzaA
GSM2545378 CNS_RNA-seq_742 GSM2545378 Mus musculus 8 weeks Male InfluenzaA
GSM2545379 CNS_RNA-seq_743 GSM2545379 Mus musculus 8 weeks Male InfluenzaA
strain time tissue mouse
GSM2545355 C57BL/6 Day4 Spinalcord 1
GSM2545356 C57BL/6 Day0 Spinalcord 2
GSM2545357 C57BL/6 Day0 Spinalcord 3
GSM2545360 C57BL/6 Day8 Spinalcord 6
GSM2545361 C57BL/6 Day0 Spinalcord 7
GSM2545367 C57BL/6 Day0 Spinalcord 11
GSM2545368 C57BL/6 Day4 Spinalcord 12
GSM2545369 C57BL/6 Day4 Spinalcord 13
GSM2545372 C57BL/6 Day8 Spinalcord 17
GSM2545373 C57BL/6 Day4 Spinalcord 18
GSM2545378 C57BL/6 Day8 Spinalcord 23
GSM2545379 C57BL/6 Day8 Spinalcord 24R
vd <- VisualizeDesign(sampleData = meta_male_spc, designFormula = ~ time)
vd$designmatrix
OUTPUT
(Intercept) timeDay4 timeDay8
GSM2545355 1 1 0
GSM2545356 1 0 0
GSM2545357 1 0 0
GSM2545360 1 0 1
GSM2545361 1 0 0
GSM2545367 1 0 0
GSM2545368 1 1 0
GSM2545369 1 1 0
GSM2545372 1 0 1
GSM2545373 1 1 0
GSM2545378 1 0 1
GSM2545379 1 0 1R
vd$plotlist
OUTPUT
[[1]]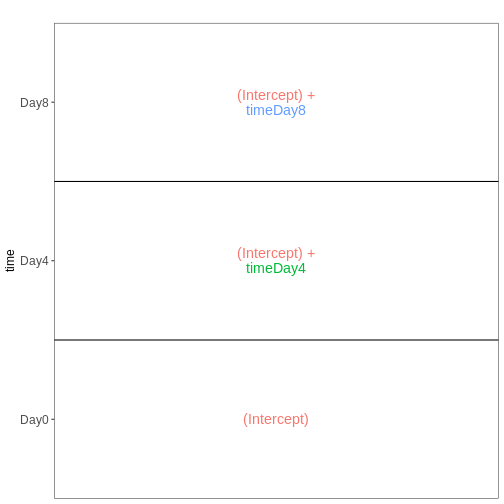
Factorial design without interactions
Next, we again consider only non-infected mice, but fit a model incorporating both sex and tissue as predictors. We assume that the tissue differences are the same for both male and female mice, and consequently fit an additive model, without interaction terms.
R
meta_noninf <- meta %>% filter(time == "Day0")
meta_noninf
OUTPUT
title geo_accession organism age sex
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545343 CNS_RNA-seq_20C GSM2545343 Mus musculus 8 weeks Male
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545349 CNS_RNA-seq_28C GSM2545349 Mus musculus 8 weeks Male
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545354 CNS_RNA-seq_4C GSM2545354 Mus musculus 8 weeks Male
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
infection strain time tissue mouse
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10
GSM2545343 NonInfected C57BL/6 Day0 Cerebellum 11
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8
GSM2545349 NonInfected C57BL/6 Day0 Cerebellum 7
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4
GSM2545354 NonInfected C57BL/6 Day0 Cerebellum 2
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11R
vd <- VisualizeDesign(sampleData = meta_noninf,
designFormula = ~ sex + tissue)
vd$designmatrix
OUTPUT
(Intercept) sexMale tissueSpinalcord
GSM2545337 1 0 0
GSM2545338 1 0 0
GSM2545343 1 1 0
GSM2545348 1 0 0
GSM2545349 1 1 0
GSM2545353 1 0 0
GSM2545354 1 1 0
GSM2545356 1 1 1
GSM2545357 1 1 1
GSM2545358 1 0 1
GSM2545361 1 1 1
GSM2545364 1 0 1
GSM2545365 1 0 1
GSM2545366 1 0 1
GSM2545367 1 1 1R
vd$plotlist
OUTPUT
[[1]]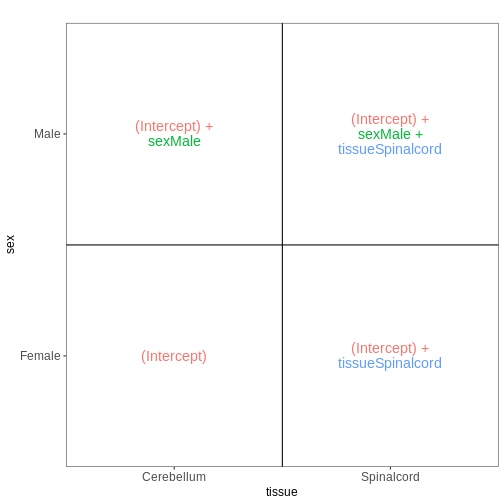
Factorial design with interactions
In the previous model, we assumed that the tissue differences were the same for both male and female mice. To allow for the estimation of sex-specific tissue differences (at the expense of having one additional coefficient to estimate from the data), we can include an interaction term in the model.
R
meta_noninf <- meta %>% filter(time == "Day0")
meta_noninf
OUTPUT
title geo_accession organism age sex
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545343 CNS_RNA-seq_20C GSM2545343 Mus musculus 8 weeks Male
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545349 CNS_RNA-seq_28C GSM2545349 Mus musculus 8 weeks Male
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545354 CNS_RNA-seq_4C GSM2545354 Mus musculus 8 weeks Male
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
infection strain time tissue mouse
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10
GSM2545343 NonInfected C57BL/6 Day0 Cerebellum 11
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8
GSM2545349 NonInfected C57BL/6 Day0 Cerebellum 7
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4
GSM2545354 NonInfected C57BL/6 Day0 Cerebellum 2
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11R
## Define a design including an interaction term
## Note that ~ sex * tissue is equivalent to
## ~ sex + tissue + sex:tissue
vd <- VisualizeDesign(sampleData = meta_noninf,
designFormula = ~ sex * tissue)
vd$designmatrix
OUTPUT
(Intercept) sexMale tissueSpinalcord sexMale:tissueSpinalcord
GSM2545337 1 0 0 0
GSM2545338 1 0 0 0
GSM2545343 1 1 0 0
GSM2545348 1 0 0 0
GSM2545349 1 1 0 0
GSM2545353 1 0 0 0
GSM2545354 1 1 0 0
GSM2545356 1 1 1 1
GSM2545357 1 1 1 1
GSM2545358 1 0 1 0
GSM2545361 1 1 1 1
GSM2545364 1 0 1 0
GSM2545365 1 0 1 0
GSM2545366 1 0 1 0
GSM2545367 1 1 1 1R
vd$plotlist
OUTPUT
[[1]]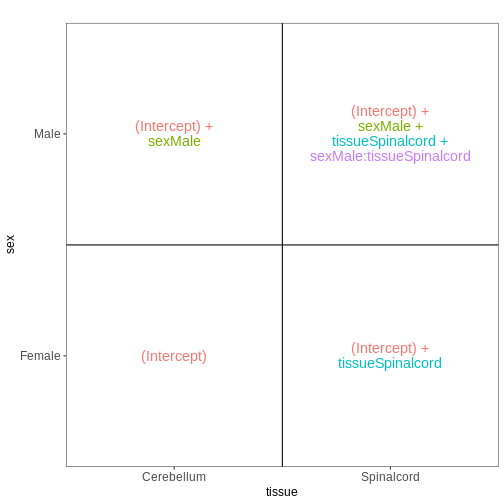
Combining multiple factors into one
Sometimes, for experiments with multiple factors, it is easier to interpret coefficients and set up contrasts of interest if the factors are combined into one. Let’s consider the previous example again, using this approach:
R
meta_noninf <- meta %>% filter(time == "Day0")
meta_noninf$sex_tissue <- paste0(meta_noninf$sex, "_", meta_noninf$tissue)
meta_noninf
OUTPUT
title geo_accession organism age sex
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545343 CNS_RNA-seq_20C GSM2545343 Mus musculus 8 weeks Male
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545349 CNS_RNA-seq_28C GSM2545349 Mus musculus 8 weeks Male
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545354 CNS_RNA-seq_4C GSM2545354 Mus musculus 8 weeks Male
GSM2545356 CNS_RNA-seq_574 GSM2545356 Mus musculus 8 weeks Male
GSM2545357 CNS_RNA-seq_575 GSM2545357 Mus musculus 8 weeks Male
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545361 CNS_RNA-seq_590 GSM2545361 Mus musculus 8 weeks Male
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545367 CNS_RNA-seq_713 GSM2545367 Mus musculus 8 weeks Male
infection strain time tissue mouse sex_tissue
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9 Female_Cerebellum
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10 Female_Cerebellum
GSM2545343 NonInfected C57BL/6 Day0 Cerebellum 11 Male_Cerebellum
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8 Female_Cerebellum
GSM2545349 NonInfected C57BL/6 Day0 Cerebellum 7 Male_Cerebellum
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4 Female_Cerebellum
GSM2545354 NonInfected C57BL/6 Day0 Cerebellum 2 Male_Cerebellum
GSM2545356 NonInfected C57BL/6 Day0 Spinalcord 2 Male_Spinalcord
GSM2545357 NonInfected C57BL/6 Day0 Spinalcord 3 Male_Spinalcord
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4 Female_Spinalcord
GSM2545361 NonInfected C57BL/6 Day0 Spinalcord 7 Male_Spinalcord
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8 Female_Spinalcord
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9 Female_Spinalcord
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10 Female_Spinalcord
GSM2545367 NonInfected C57BL/6 Day0 Spinalcord 11 Male_SpinalcordR
vd <- VisualizeDesign(sampleData = meta_noninf,
designFormula = ~ 0 + sex_tissue)
vd$designmatrix
OUTPUT
sex_tissueFemale_Cerebellum sex_tissueFemale_Spinalcord
GSM2545337 1 0
GSM2545338 1 0
GSM2545343 0 0
GSM2545348 1 0
GSM2545349 0 0
GSM2545353 1 0
GSM2545354 0 0
GSM2545356 0 0
GSM2545357 0 0
GSM2545358 0 1
GSM2545361 0 0
GSM2545364 0 1
GSM2545365 0 1
GSM2545366 0 1
GSM2545367 0 0
sex_tissueMale_Cerebellum sex_tissueMale_Spinalcord
GSM2545337 0 0
GSM2545338 0 0
GSM2545343 1 0
GSM2545348 0 0
GSM2545349 1 0
GSM2545353 0 0
GSM2545354 1 0
GSM2545356 0 1
GSM2545357 0 1
GSM2545358 0 0
GSM2545361 0 1
GSM2545364 0 0
GSM2545365 0 0
GSM2545366 0 0
GSM2545367 0 1R
vd$plotlist
OUTPUT
[[1]]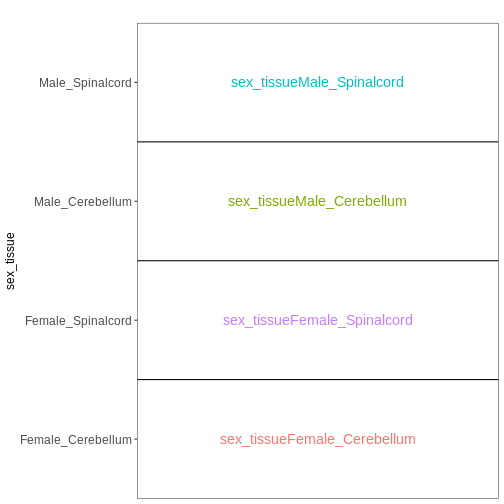
Paired design
In this particular data set the samples are paired - the same mice have contributed both the cerebellum and spinal cord samples. This information was not included in the previous models. However, accounting for it can increase power to detect tissue differences by eliminating variability in baseline expression levels between mice. Here, we define a paired design for the female non-infected mice, aimed at testing for differences between tissues after accounting for baseline differences between mice.
R
meta_fem_day0 <- meta %>% filter(sex == "Female" &
time == "Day0")
# ensure that mouse is treated as a categorical variable
meta_fem_day0$mouse <- factor(meta_fem_day0$mouse)
meta_fem_day0
OUTPUT
title geo_accession organism age sex
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
infection strain time tissue mouse
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10R
vd <- VisualizeDesign(sampleData = meta_fem_day0,
designFormula = ~ mouse + tissue)
vd$designmatrix
OUTPUT
(Intercept) mouse8 mouse9 mouse10 tissueSpinalcord
GSM2545337 1 0 1 0 0
GSM2545338 1 0 0 1 0
GSM2545348 1 1 0 0 0
GSM2545353 1 0 0 0 0
GSM2545358 1 0 0 0 1
GSM2545364 1 1 0 0 1
GSM2545365 1 0 1 0 1
GSM2545366 1 0 0 1 1R
vd$plotlist
OUTPUT
[[1]]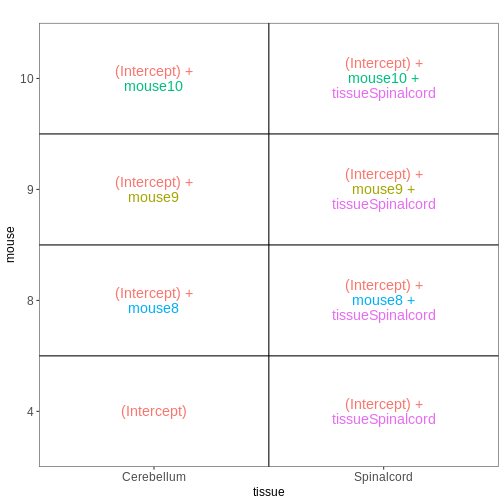
Within- and between-subject comparisons
In some situations, we need to combine the types of models considered above. For example, let’s say that we want to investigate if the tissue differences are different for infected and non-infected female mice. In this case, each mice only contributes to one of the infection groups (each mice is either infected or non-infected), but contributes both a cerebellum and a spinal cord sample. One way to view this type of design is as two paired experiments, one for each infection group (see the edgeR user guide section 3.5). We can then easily compare the two tissues in each infection group, and contrast the tissue differences between the infection groups.
R
meta_fem_day04 <- meta %>%
filter(sex == "Female" &
time %in% c("Day0", "Day4")) %>%
droplevels()
# ensure that mouse is treated as a categorical variable
meta_fem_day04$mouse <- factor(meta_fem_day04$mouse)
meta_fem_day04
OUTPUT
title geo_accession organism age sex
GSM2545337 CNS_RNA-seq_11C GSM2545337 Mus musculus 8 weeks Female
GSM2545338 CNS_RNA-seq_12C GSM2545338 Mus musculus 8 weeks Female
GSM2545339 CNS_RNA-seq_13C GSM2545339 Mus musculus 8 weeks Female
GSM2545344 CNS_RNA-seq_21C GSM2545344 Mus musculus 8 weeks Female
GSM2545348 CNS_RNA-seq_27C GSM2545348 Mus musculus 8 weeks Female
GSM2545352 CNS_RNA-seq_30C GSM2545352 Mus musculus 8 weeks Female
GSM2545353 CNS_RNA-seq_3C GSM2545353 Mus musculus 8 weeks Female
GSM2545358 CNS_RNA-seq_583 GSM2545358 Mus musculus 8 weeks Female
GSM2545362 CNS_RNA-seq_5C GSM2545362 Mus musculus 8 weeks Female
GSM2545364 CNS_RNA-seq_709 GSM2545364 Mus musculus 8 weeks Female
GSM2545365 CNS_RNA-seq_710 GSM2545365 Mus musculus 8 weeks Female
GSM2545366 CNS_RNA-seq_711 GSM2545366 Mus musculus 8 weeks Female
GSM2545371 CNS_RNA-seq_731 GSM2545371 Mus musculus 8 weeks Female
GSM2545375 CNS_RNA-seq_738 GSM2545375 Mus musculus 8 weeks Female
GSM2545376 CNS_RNA-seq_740 GSM2545376 Mus musculus 8 weeks Female
GSM2545377 CNS_RNA-seq_741 GSM2545377 Mus musculus 8 weeks Female
infection strain time tissue mouse
GSM2545337 NonInfected C57BL/6 Day0 Cerebellum 9
GSM2545338 NonInfected C57BL/6 Day0 Cerebellum 10
GSM2545339 InfluenzaA C57BL/6 Day4 Cerebellum 15
GSM2545344 InfluenzaA C57BL/6 Day4 Cerebellum 22
GSM2545348 NonInfected C57BL/6 Day0 Cerebellum 8
GSM2545352 InfluenzaA C57BL/6 Day4 Cerebellum 21
GSM2545353 NonInfected C57BL/6 Day0 Cerebellum 4
GSM2545358 NonInfected C57BL/6 Day0 Spinalcord 4
GSM2545362 InfluenzaA C57BL/6 Day4 Cerebellum 20
GSM2545364 NonInfected C57BL/6 Day0 Spinalcord 8
GSM2545365 NonInfected C57BL/6 Day0 Spinalcord 9
GSM2545366 NonInfected C57BL/6 Day0 Spinalcord 10
GSM2545371 InfluenzaA C57BL/6 Day4 Spinalcord 15
GSM2545375 InfluenzaA C57BL/6 Day4 Spinalcord 20
GSM2545376 InfluenzaA C57BL/6 Day4 Spinalcord 21
GSM2545377 InfluenzaA C57BL/6 Day4 Spinalcord 22R
design <- model.matrix(~ mouse, data = meta_fem_day04)
design <- cbind(design,
Spc.Day0 = meta_fem_day04$tissue == "Spinalcord" &
meta_fem_day04$time == "Day0",
Spc.Day4 = meta_fem_day04$tissue == "Spinalcord" &
meta_fem_day04$time == "Day4")
rownames(design) <- rownames(meta_fem_day04)
design
OUTPUT
(Intercept) mouse8 mouse9 mouse10 mouse15 mouse20 mouse21 mouse22
GSM2545337 1 0 1 0 0 0 0 0
GSM2545338 1 0 0 1 0 0 0 0
GSM2545339 1 0 0 0 1 0 0 0
GSM2545344 1 0 0 0 0 0 0 1
GSM2545348 1 1 0 0 0 0 0 0
GSM2545352 1 0 0 0 0 0 1 0
GSM2545353 1 0 0 0 0 0 0 0
GSM2545358 1 0 0 0 0 0 0 0
GSM2545362 1 0 0 0 0 1 0 0
GSM2545364 1 1 0 0 0 0 0 0
GSM2545365 1 0 1 0 0 0 0 0
GSM2545366 1 0 0 1 0 0 0 0
GSM2545371 1 0 0 0 1 0 0 0
GSM2545375 1 0 0 0 0 1 0 0
GSM2545376 1 0 0 0 0 0 1 0
GSM2545377 1 0 0 0 0 0 0 1
Spc.Day0 Spc.Day4
GSM2545337 0 0
GSM2545338 0 0
GSM2545339 0 0
GSM2545344 0 0
GSM2545348 0 0
GSM2545352 0 0
GSM2545353 0 0
GSM2545358 1 0
GSM2545362 0 0
GSM2545364 1 0
GSM2545365 1 0
GSM2545366 1 0
GSM2545371 0 1
GSM2545375 0 1
GSM2545376 0 1
GSM2545377 0 1R
vd <- VisualizeDesign(sampleData = meta_fem_day04 %>%
select(time, tissue, mouse),
designFormula = NULL,
designMatrix = design, flipCoordFitted = FALSE)
vd$designmatrix
OUTPUT
(Intercept) mouse8 mouse9 mouse10 mouse15 mouse20 mouse21 mouse22
GSM2545337 1 0 1 0 0 0 0 0
GSM2545338 1 0 0 1 0 0 0 0
GSM2545339 1 0 0 0 1 0 0 0
GSM2545344 1 0 0 0 0 0 0 1
GSM2545348 1 1 0 0 0 0 0 0
GSM2545352 1 0 0 0 0 0 1 0
GSM2545353 1 0 0 0 0 0 0 0
GSM2545358 1 0 0 0 0 0 0 0
GSM2545362 1 0 0 0 0 1 0 0
GSM2545364 1 1 0 0 0 0 0 0
GSM2545365 1 0 1 0 0 0 0 0
GSM2545366 1 0 0 1 0 0 0 0
GSM2545371 1 0 0 0 1 0 0 0
GSM2545375 1 0 0 0 0 1 0 0
GSM2545376 1 0 0 0 0 0 1 0
GSM2545377 1 0 0 0 0 0 0 1
Spc.Day0 Spc.Day4
GSM2545337 0 0
GSM2545338 0 0
GSM2545339 0 0
GSM2545344 0 0
GSM2545348 0 0
GSM2545352 0 0
GSM2545353 0 0
GSM2545358 1 0
GSM2545362 0 0
GSM2545364 1 0
GSM2545365 1 0
GSM2545366 1 0
GSM2545371 0 1
GSM2545375 0 1
GSM2545376 0 1
GSM2545377 0 1R
vd$plotlist
OUTPUT
$`time = Day0`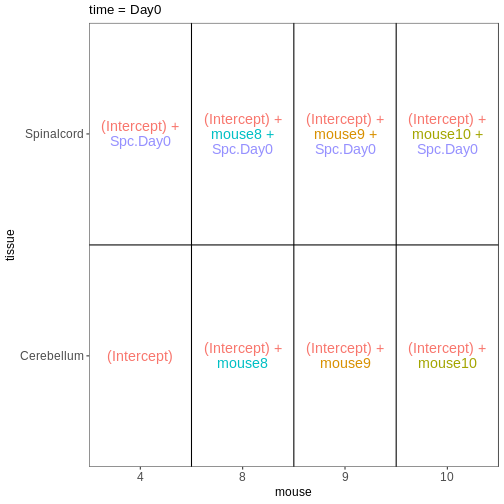
OUTPUT
$`time = Day4`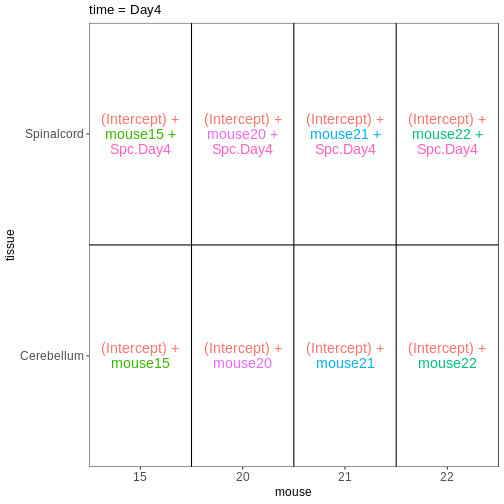
How does this relate to the DESeq2 analysis we did in the previous episode?
Now that we have learnt more about interpreting design matrices, let’s look back to the differential expression analysis we performed in the previous episode. We will repeat the main lines of code here.
R
se <- readRDS("data/GSE96870_se.rds")
se <- se[rowSums(assay(se, "counts")) > 5, ]
dds <- DESeq2::DESeqDataSet(se, design = ~ sex + time)
dds <- DESeq(dds)
OUTPUT
estimating size factorsOUTPUT
estimating dispersionsOUTPUT
gene-wise dispersion estimatesOUTPUT
mean-dispersion relationshipOUTPUT
final dispersion estimatesOUTPUT
fitting model and testingDESeq2 stores the design matrix in the object:
R
attr(dds, "modelMatrix")
OUTPUT
Intercept sex_Male_vs_Female time_Day4_vs_Day0 time_Day8_vs_Day0
Female_Day0_9 1 0 0 0
Female_Day0_10 1 0 0 0
Female_Day0_8 1 0 0 0
Female_Day0_4 1 0 0 0
Male_Day0_11 1 1 0 0
Male_Day0_7 1 1 0 0
Male_Day0_2 1 1 0 0
Female_Day4_15 1 0 1 0
Female_Day4_22 1 0 1 0
Female_Day4_21 1 0 1 0
Female_Day4_20 1 0 1 0
Male_Day4_18 1 1 1 0
Male_Day4_13 1 1 1 0
Male_Day4_1 1 1 1 0
Male_Day4_12 1 1 1 0
Female_Day8_14 1 0 0 1
Female_Day8_5 1 0 0 1
Female_Day8_16 1 0 0 1
Female_Day8_19 1 0 0 1
Male_Day8_6 1 1 0 1
Male_Day8_23 1 1 0 1
Male_Day8_24 1 1 0 1
attr(,"assign")
[1] 0 1 2 2
attr(,"contrasts")
attr(,"contrasts")$sex
[1] "contr.treatment"
attr(,"contrasts")$time
[1] "contr.treatment"The column names can be obtained via the resultsNames
function:
R
resultsNames(dds)
OUTPUT
[1] "Intercept" "sex_Male_vs_Female" "time_Day4_vs_Day0"
[4] "time_Day8_vs_Day0" Let’s visualize this design:
R
vd <- VisualizeDesign(sampleData = colData(dds)[, c("sex", "time")],
designMatrix = attr(dds, "modelMatrix"),
flipCoordFitted = TRUE)
vd$plotlist
OUTPUT
[[1]]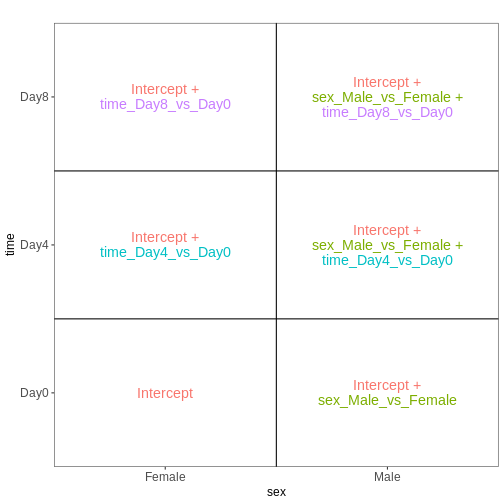
In the previous episode, we performed a test comparing Day8 samples to Day0 samples:
R
resTime <- results(dds, contrast = c("time", "Day8", "Day0"))
From the figure above, we see that this comparison is represented by
the time_Day8_vs_Day0 coefficient, which corresponds to the
fourth column in the design matrix. Thus, an alternative way of
specifying the contrast for the test would be:
R
resTimeNum <- results(dds, contrast = c(0, 0, 0, 1))
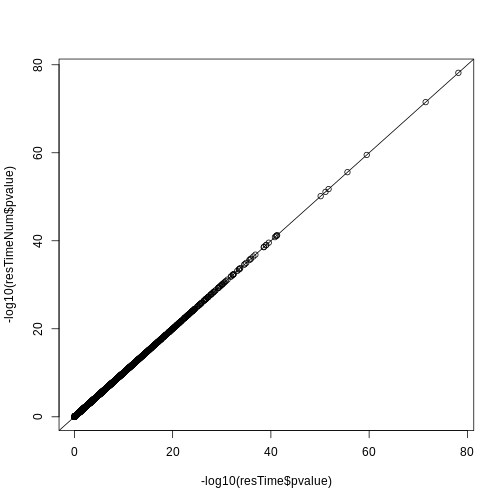
Let’s check if the results are comparable:
R
summary(resTime)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 4472, 16%
LFC < 0 (down) : 4282, 16%
outliers [1] : 10, 0.036%
low counts [2] : 3723, 14%
(mean count < 1)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
summary(resTimeNum)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 4472, 16%
LFC < 0 (down) : 4282, 16%
outliers [1] : 10, 0.036%
low counts [2] : 3723, 14%
(mean count < 1)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
## logFC
plot(resTime$log2FoldChange, resTimeNum$log2FoldChange)
abline(0, 1)
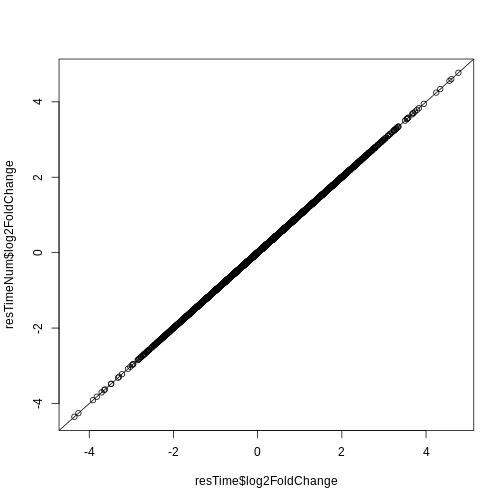
R
## -log10(p-value)
plot(-log10(resTime$pvalue), -log10(resTimeNum$pvalue))
abline(0, 1)
Redo DESeq2 analysis with interaction
Next, let’s look at a different setup. We still consider the sex and time predictors, but now we allow an interaction between them. In other words, we allow the time effect to be different for males and females.
R
se <- readRDS("data/GSE96870_se.rds")
se <- se[rowSums(assay(se, "counts")) > 5, ]
dds <- DESeq2::DESeqDataSet(se, design = ~ sex * time)
dds <- DESeq(dds)
OUTPUT
estimating size factorsOUTPUT
estimating dispersionsOUTPUT
gene-wise dispersion estimatesOUTPUT
mean-dispersion relationshipOUTPUT
final dispersion estimatesOUTPUT
fitting model and testingR
attr(dds, "modelMatrix")
OUTPUT
Intercept sex_Male_vs_Female time_Day4_vs_Day0 time_Day8_vs_Day0
Female_Day0_9 1 0 0 0
Female_Day0_10 1 0 0 0
Female_Day0_8 1 0 0 0
Female_Day0_4 1 0 0 0
Male_Day0_11 1 1 0 0
Male_Day0_7 1 1 0 0
Male_Day0_2 1 1 0 0
Female_Day4_15 1 0 1 0
Female_Day4_22 1 0 1 0
Female_Day4_21 1 0 1 0
Female_Day4_20 1 0 1 0
Male_Day4_18 1 1 1 0
Male_Day4_13 1 1 1 0
Male_Day4_1 1 1 1 0
Male_Day4_12 1 1 1 0
Female_Day8_14 1 0 0 1
Female_Day8_5 1 0 0 1
Female_Day8_16 1 0 0 1
Female_Day8_19 1 0 0 1
Male_Day8_6 1 1 0 1
Male_Day8_23 1 1 0 1
Male_Day8_24 1 1 0 1
sexMale.timeDay4 sexMale.timeDay8
Female_Day0_9 0 0
Female_Day0_10 0 0
Female_Day0_8 0 0
Female_Day0_4 0 0
Male_Day0_11 0 0
Male_Day0_7 0 0
Male_Day0_2 0 0
Female_Day4_15 0 0
Female_Day4_22 0 0
Female_Day4_21 0 0
Female_Day4_20 0 0
Male_Day4_18 1 0
Male_Day4_13 1 0
Male_Day4_1 1 0
Male_Day4_12 1 0
Female_Day8_14 0 0
Female_Day8_5 0 0
Female_Day8_16 0 0
Female_Day8_19 0 0
Male_Day8_6 0 1
Male_Day8_23 0 1
Male_Day8_24 0 1
attr(,"assign")
[1] 0 1 2 2 3 3
attr(,"contrasts")
attr(,"contrasts")$sex
[1] "contr.treatment"
attr(,"contrasts")$time
[1] "contr.treatment"Let’s visualize this design:
R
vd <- VisualizeDesign(sampleData = colData(dds)[, c("sex", "time")],
designMatrix = attr(dds, "modelMatrix"),
flipCoordFitted = TRUE)
vd$plotlist
OUTPUT
[[1]]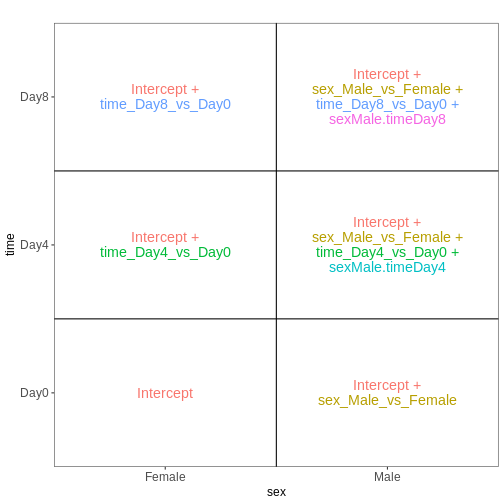
Note that now, the time_Day8_vs_Day0 coefficient
represents the difference between Day8 and Day0 for the Female
samples. To get the corresponding difference for the male
samples, we need to also add the interaction effect
(sexMale.timeDay8).
R
## Day8 vs Day0, female
resTimeFemale <- results(dds, contrast = c("time", "Day8", "Day0"))
## Interaction effect (difference in Day8-Day0 effect between Male and Female)
resTimeInt <- results(dds, name = "sexMale.timeDay8")
Let’s try to fit this model with the second approach mentioned above, namely to create a single factor.
R
se <- readRDS("data/GSE96870_se.rds")
se <- se[rowSums(assay(se, "counts")) > 5, ]
se$sex_time <- paste0(se$sex, "_", se$time)
dds <- DESeq2::DESeqDataSet(se, design = ~ 0 + sex_time)
dds <- DESeq(dds)
OUTPUT
estimating size factorsOUTPUT
estimating dispersionsOUTPUT
gene-wise dispersion estimatesOUTPUT
mean-dispersion relationshipOUTPUT
final dispersion estimatesOUTPUT
fitting model and testingR
attr(dds, "modelMatrix")
OUTPUT
sex_timeFemale_Day0 sex_timeFemale_Day4 sex_timeFemale_Day8
Female_Day0_9 1 0 0
Female_Day0_10 1 0 0
Female_Day0_8 1 0 0
Female_Day0_4 1 0 0
Male_Day0_11 0 0 0
Male_Day0_7 0 0 0
Male_Day0_2 0 0 0
Female_Day4_15 0 1 0
Female_Day4_22 0 1 0
Female_Day4_21 0 1 0
Female_Day4_20 0 1 0
Male_Day4_18 0 0 0
Male_Day4_13 0 0 0
Male_Day4_1 0 0 0
Male_Day4_12 0 0 0
Female_Day8_14 0 0 1
Female_Day8_5 0 0 1
Female_Day8_16 0 0 1
Female_Day8_19 0 0 1
Male_Day8_6 0 0 0
Male_Day8_23 0 0 0
Male_Day8_24 0 0 0
sex_timeMale_Day0 sex_timeMale_Day4 sex_timeMale_Day8
Female_Day0_9 0 0 0
Female_Day0_10 0 0 0
Female_Day0_8 0 0 0
Female_Day0_4 0 0 0
Male_Day0_11 1 0 0
Male_Day0_7 1 0 0
Male_Day0_2 1 0 0
Female_Day4_15 0 0 0
Female_Day4_22 0 0 0
Female_Day4_21 0 0 0
Female_Day4_20 0 0 0
Male_Day4_18 0 1 0
Male_Day4_13 0 1 0
Male_Day4_1 0 1 0
Male_Day4_12 0 1 0
Female_Day8_14 0 0 0
Female_Day8_5 0 0 0
Female_Day8_16 0 0 0
Female_Day8_19 0 0 0
Male_Day8_6 0 0 1
Male_Day8_23 0 0 1
Male_Day8_24 0 0 1
attr(,"assign")
[1] 1 1 1 1 1 1
attr(,"contrasts")
attr(,"contrasts")$sex_time
[1] "contr.treatment"We again visualize this design:
R
vd <- VisualizeDesign(sampleData = colData(dds)[, c("sex", "time")],
designMatrix = attr(dds, "modelMatrix"),
flipCoordFitted = TRUE)
vd$plotlist
OUTPUT
[[1]]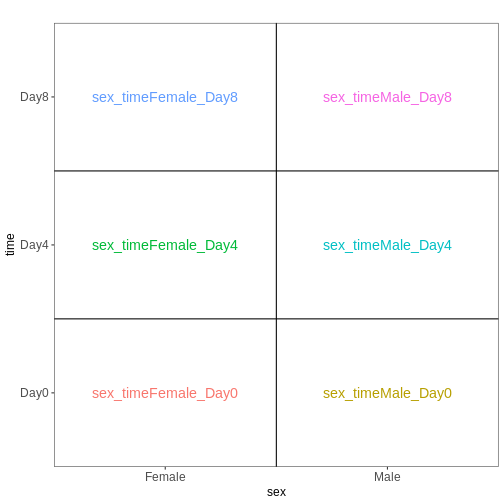
We then set up the same contrasts as above
R
## Day8 vs Day0, female
resTimeFemaleSingle <- results(dds, contrast = c("sex_time", "Female_Day8", "Female_Day0"))
## Interaction effect (difference in Day8-Day0 effect between Male and Female)
resultsNames(dds)
OUTPUT
[1] "sex_timeFemale_Day0" "sex_timeFemale_Day4" "sex_timeFemale_Day8"
[4] "sex_timeMale_Day0" "sex_timeMale_Day4" "sex_timeMale_Day8" R
resTimeIntSingle <- results(dds, contrast = c(1, 0, -1, -1, 0, 1))
Check that these results agree with the ones obtained by fitting the model with the two factors and the interaction term.
R
summary(resTimeFemale)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 2969, 11%
LFC < 0 (down) : 3218, 12%
outliers [1] : 6, 0.022%
low counts [2] : 6382, 23%
(mean count < 3)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
summary(resTimeFemaleSingle)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 2969, 11%
LFC < 0 (down) : 3218, 12%
outliers [1] : 6, 0.022%
low counts [2] : 6382, 23%
(mean count < 3)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
plot(-log10(resTimeFemale$pvalue), -log10(resTimeFemaleSingle$pvalue))
abline(0, 1)
R
summary(resTimeInt)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 0, 0%
LFC < 0 (down) : 0, 0%
outliers [1] : 6, 0.022%
low counts [2] : 0, 0%
(mean count < 0)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
summary(resTimeIntSingle)
OUTPUT
out of 27430 with nonzero total read count
adjusted p-value < 0.1
LFC > 0 (up) : 0, 0%
LFC < 0 (down) : 0, 0%
outliers [1] : 6, 0.022%
low counts [2] : 0, 0%
(mean count < 0)
[1] see 'cooksCutoff' argument of ?results
[2] see 'independentFiltering' argument of ?resultsR
plot(-log10(resTimeInt$pvalue), -log10(resTimeIntSingle$pvalue))
abline(0, 1)
Key Points
- The formula framework in R allows creation of design matrices, which details the variables expected to be associated with systematic differences in gene expression levels.
- Comparisons of interest can be defined using contrasts, which are linear combinations of the model coefficients.