Control flow

Last updated on 2023-08-17 | Edit this page

Overview

Questions

“What are for and while loops?”
“How to use conditionals?”
“What is an interface?”

Objectives

Conditionals

Before starting to work in a new document, Melissa has to:

Activate her environment

JULIA

using Pkg
Pkg.activate(joinpath(@__DIR__, "projects", "trebuchet"))
Pkg.instantiate()

OUTPUT

  Activating project at `~/projects/trebuchet`

Importing the package under its modified name

JULIA

import Trebuchet as Trebuchets

Defining the structures

JULIA

mutable struct Trebuchet <: AbstractVector{Float64}
  counterweight::Float64
  release_angle::Float64
end

struct Environment
  wind::Float64
  target_distance::Float64
end

Now that Melissa knows which method to add she thinks about the implementation.

If the index is 1 she wants to set counterweight while if the index is 2 she wants to set release_angle and since these are the only two fields she wants to return an error if anything else comes in. In Julia the keywords to specify conditions are if, elseif and else, closed with an end. Thus she writes

JULIA

function Base.setindex!(trebuchet::Trebuchet, v, i::Int)
    if i === 1
        trebuchet.counterweight = v
    elseif i === 2
        trebuchet.release_angle = v
    else
        error("Trebuchet only accepts indices 1 and 2, yours is $i")
    end
end

Interfaces

setindex! is actually one function of a widespread interface in the Julia language: AbstractArrays. An interface is a collection of methods that are all implemented by a certain type. For example, the Julia manual lists all methods that a subtype of AbstractArray need to implement to adhere to the AbstractArray interface:

size(A) returns a tuple containing the dimensions of A
getindex(A, i::Int) returns the value associated with index i
setindex!(A, v, i::Int) writes a new value v at the index i

If Melissa implements this interface for the Trebuchet type, it will work with every function in Base that accepts an AbstractArray.

She also needs to make Trebuchet a proper subtype of AbstractArray as she tried in the types episode. Therefore she restarts her REPL and redefines Trebuchet and Environment, as well as the slurp-and-splat shoot_distance function:

JULIA

using Pkg
Pkg.activate("projects/trebuchet")

import Trebuchet as Trebuchets

mutable struct Trebuchet <: AbstractVector{Float64}
  counterweight::Float64
  release_angle::Float64
end

struct Environment
    wind::Float64
    target_distance::Float64
end

function shoot_distance(args...)
    Trebuchets.shoot(args...)[2]
end

function shoot_distance(trebuchet::Trebuchet, env::Environment)
     shoot_distance(env.wind, trebuchet.release_angle, trebuchet.counterweight)
end

OUTPUT

shoot_distance (generic function with 2 methods)

Then she goes about implementing the AbstractArray interface.

Implement the `AbstractArray` interface for `Trebuchet`

Now we know enough to actually implement the AbstractArray interface. You don’t need to implement the optional methods.

Hint: Take a look at the docstrings of getfield and tuple.

Show me the solution

JULIA

Base.size(trebuchet::Trebuchet) = tuple(2)
Base.getindex(trebuchet::Trebuchet, i::Int) = getfield(trebuchet, i)
function Base.setindex!(trebuchet::Trebuchet, v, i::Int)
     if i === 1
         trebuchet.counterweight = v
    elseif i === 2
        trebuchet.release_angle = v
    else
        error("Trebuchet only accepts indices 1 and 2, yours is $i")
    end
end

With the new Trebuchet defined with a complete AbstractArray interface, Melissa tries again to modify a counterweight by index:

JULIA

trebuchet = Trebuchet(500, 0.25pi)

OUTPUT

2-element Trebuchet:
 500.0
   0.7853981633974483

JULIA

trebuchet[1] = 2

OUTPUT

JULIA

trebuchet

OUTPUT

2-element Trebuchet:
 2.0
 0.7853981633974483

Loops

Now Melissa knows how to shoot the virtual trebuchet and get the distance of the projectile, but in order to aim she needs to take a lot of trial shots in a row. She wants her trebuchet to only shoot a hundred meters.

She could execute the function several times on the REPL with different parameters, but that gets tiresome quickly. A better way to do this is to use loops.

But first Melissa needs a way to improve her parameters.

Digression: Gradients

The shoot_distance function takes three input parameters and returns one value (the distance). Whenever we change one of the input parameters, we will get a different distance.

The gradient of a function gives the direction in which the return value will change when each input value changes.

Since the shoot_distance function has three input parameters, the gradient of shoot_distance will return a 3-element Array: one direction for each input parameter.

Thanks to automatic differentiation and the Julia package ForwardDiff.jl gradients can be calculated easily.

Melissa uses the gradient function of ForwardDiff.jl to get the direction in which she needs to change the parameters to make the largest difference.

Do you remember?

What does Melissa need to write into the REPL to install the package ForwardDiff?

] install ForwardDiff
add ForwardDiff
] add ForwardDiff.jl
] add ForwardDiff

Show me the solution

The correct solution is 4: ] to enter pkg mode, then

JULIA

pkg> add ForwardDiff

JULIA

using ForwardDiff: gradient


imprecise_trebuchet = Trebuchet(500.0, 0.25pi);
environment = Environment(5.0, 100.0);

grad = gradient(x ->(shoot_distance([environment.wind, x[2], x[1]])
                      - environment.target_distance),
                imprecise_trebuchet)

OUTPUT

2-element Vector{Float64}:
  -0.12516519503998055
 -49.443442438172205

Melissa now changes her arguments a little bit in the direction of the gradient and checks the new distance.

JULIA

better_trebuchet = imprecise_trebuchet - 0.05 * grad;

shoot_distance([5, better_trebuchet[2], better_trebuchet[1]])

OUTPUT

-2.785549535224487

Great! That didn’t shoot past the target, but instead it landed a bit too short.

Experiment

How far can you change the parameters in the direction of the gradient, such that it still improves the distance?

Try a bunch of values!

JULIA

better_trebuchet = imprecise_trebuchet - 0.04 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
120.48753521261001

JULIA

better_trebuchet = imprecise_trebuchet - 0.03 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
107.80646596787481

JULIA

better_trebuchet = imprecise_trebuchet - 0.02 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
33.90699307740854

JULIA

better_trebuchet = imprecise_trebuchet - 0.025 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
75.87613276409223

Looks like the “best” trebuchet for a target 100 m away will be between 2.5% and 3% down the gradient from the imprecise trebuchet.

For loops

Now that Melissa knows it is going in the right direction she wants to automate the additional iterations. She writes a new function aim, that performs the application of the gradient N times.

JULIA

function aim(trebuchet, environment; N = 5, η = 0.05)
           better_trebuchet = copy(trebuchet)
           for _ in 1:N
               grad = gradient(x -> (shoot_distance([environment.wind, x[2], x[1]])
                                     - environment.target_distance),
                               better_trebuchet)
               better_trebuchet -= η * grad
           end
           return Trebuchet(better_trebuchet[1], better_trebuchet[2])
       end

better_trebuchet  = aim(imprecise_trebuchet, environment);

shoot_distance(environment.wind, better_trebuchet[2], better_trebuchet[1])

OUTPUT

-2.2195176928658915

Explore

Play around with different inputs of N and η. How close can you come?

Show me the solution

This is a highly non-linear system and thus very sensitive. The distances across different values for the counterweight and the release angle α look like this: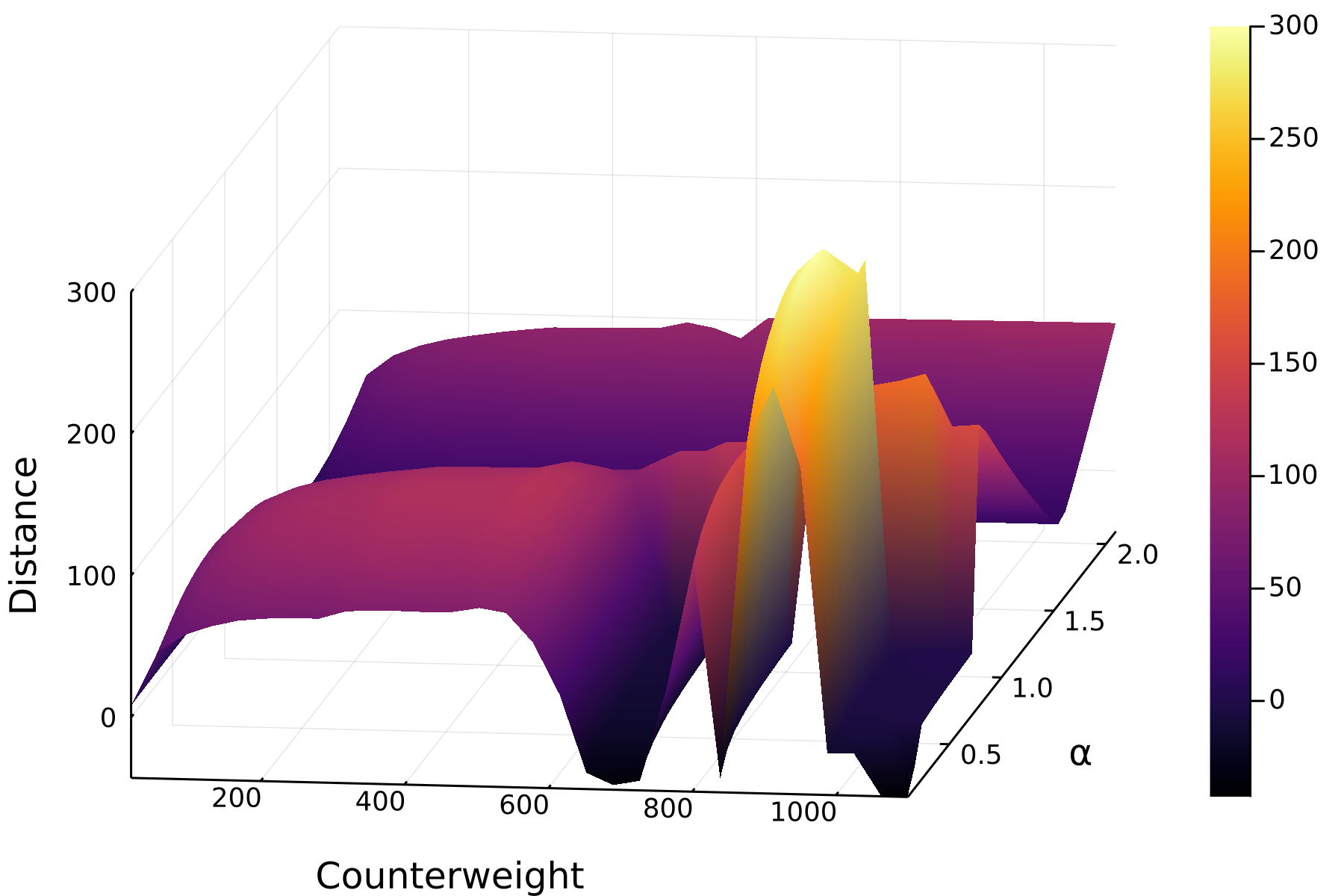

Aborting programs

If a call takes too long, you can abort it with Ctrl-c

While loops

Melissa finds the output of the above aim function too unpredictable to be useful. That’s why she decides to change it a bit. This time she uses a while-loop to run the iterations until she is sufficiently near her target.

(Hint: ε is \epsilontab, and η is \etatab.)

JULIA

function aim(trebuchet, environment; ε = 0.1, η = 0.05)
    better_trebuchet = copy(trebuchet)
    hit = x -> (shoot_distance([environment.wind, x[2], x[1]])
                          - environment.target_distance)
            while abs(hit(better_trebuchet)) > ε
                grad = gradient(hit, better_trebuchet)
                better_trebuchet -= η * grad
            end
            return Trebuchet(better_trebuchet[1], better_trebuchet[2])
        end

better_trebuchet = aim(imprecise_trebuchet, environment);

shoot_distance(better_trebuchet, environment)

OUTPUT

100.05601729579894

That is more what she had in mind. Your trebuchet may be tuned differently, but it should hit just as close as hers.

Keypoints

“Interfaces are informal”
“Use for loops for a known number of iterations and while loops for an unknown number of iterations.”
“Julia packages compose nicely.”

Control flow

Overview

Questions

Objectives

Conditionals

JULIA

OUTPUT

JULIA

JULIA

JULIA

Interfaces

JULIA

OUTPUT

Implement the AbstractArray interface for Trebuchet

Show me the solution

JULIA

JULIA

OUTPUT

JULIA

OUTPUT

JULIA

OUTPUT

Loops

Digression: Gradients

Do you remember?

Show me the solution

JULIA

JULIA

OUTPUT

JULIA

OUTPUT

Experiment

Try a bunch of values!

JULIA

JULIA

JULIA

JULIA

For loops

JULIA

OUTPUT

Explore

Show me the solution

Aborting programs

While loops

JULIA

OUTPUT

Keypoints

Implement the `AbstractArray` interface for `Trebuchet`