Loops

Last updated on 2024-11-15 | Edit this page

Overview

Questions

“What are for and while loops?”
“What is a comprehension?”

Objectives

Before starting to work in a new document, Melissa has to:

Activate her environment

JULIA

using Pkg
Pkg.activate(joinpath(@__DIR__, "projects", "trebuchet"))
Pkg.instantiate()

  Activating project at `~/projects/trebuchet`

Importing the package under its modified name

JULIA

import Trebuchet as Trebuchets

Defining the structures

JULIA

mutable struct Trebuchet <: AbstractVector{Float64}
  counterweight::Float64
  release_angle::Float64
end

struct Environment
  wind::Float64
  target_distance::Float64
end

Base.size(::Trebuchet) = tuple(2)
function Base.getindex(trebuchet::Trebuchet, i::Int)
    if i === 1
        return trebuchet.counterweight
    elseif i === 2
        return trebuchet.release_angle
    else
        error("Trebuchet only accepts indices 1 and 2, yours is $i")
    end
end
function Base.setindex!(trebuchet::Trebuchet, v, i::Int)
     if i === 1
         trebuchet.counterweight = v
    elseif i === 2
        trebuchet.release_angle = v
    else
        error("Trebuchet only accepts indices 1 and 2, yours is $i")
    end
end
function shoot_distance(trebuchet::Trebuchet, env::Environment)
     shoot_distance(env.wind, trebuchet.release_angle, trebuchet.counterweight)
end
function shoot_distance(args...) # slurping
     Trebuchets.shoot(args...)[2] # splatting
end

OUTPUT

shoot_distance (generic function with 2 methods)

Now Melissa knows how to shoot the virtual trebuchet and get the distance of the projectile, but in order to aim she needs to take a lot of trial shots in a row. She wants her trebuchet to only shoot a hundred meters.

She could execute the function several times on the REPL with different parameters, but that gets tiresome quickly. A better way to do this is to use loops.

Random search

The first thing that comes to her mind is to randomly sample points of the parameter space of the trebuchet. The function rand() will give her a random number between 0 and 1 that is uniformly distributed. So

JULIA

Trebuchet( rand() * 500, rand() * pi/2 )

OUTPUT

2-element Trebuchet:
 228.38576259167743
   1.0428133782844782

will give her a Trebuchet with a weight between 0 and 500 and a release angle between 0 and pi/2 radians at random.

Now she can store the results of 3 random trebuchets in an array like this

JULIA

env = Environment(5, 100)
distances = [shoot_distance(Trebuchet(rand() * 500, rand() * pi / 2), env) for _ in 1:3]

OUTPUT

3-element Vector{Float64}:
 75.81435701587722
 83.01842049268829
 67.14411448705451

This is called an array comprehension. To get the information of the parameters and the results in one place she writes that again a bit differently

JULIA

N = 10
weights = [rand() * 500 for _ in 1:N]
angles = [rand() * pi/2 for _ in 1:N]
distances = [(w,a) => shoot_distance(Trebuchet(w, a), env) for (w, a) in zip(weights, angles)]

OUTPUT

10-element Vector{Pair{Tuple{Float64, Float64}, Float64}}:
  (3.3334597480246253, 0.7838682352298685) => 0.6815707596179541
   (210.78228935379622, 1.381946534840864) => 35.85286633327975
   (401.5993709331619, 0.2185755446723246) => 96.9029165112703
   (174.8500444474639, 1.3802675063026215) => 34.83498096430634
   (459.5195474131575, 0.6388081196321991) => 117.62925382680423
   (325.9792258612826, 1.4742042308383514) => 23.118879918525415
 (424.04535348026496, 0.13367159006587603) => 84.32898973441384
    (367.203106692998, 0.6088354356429886) => 117.46105246416498
  (12.984772128024124, 1.5235451260228559) => 0.6815707596179541
  (10.485349585032166, 0.6353974863672037) => 0.6815707596179541

Gradient descent

That is working out so far, but Melissa wonders if she can improve her parameters more systematically.

Digression: Gradients

The shoot_distance function takes three input parameters and returns one value (the distance). Whenever we change one of the input parameters, we will get a different distance.

The gradient of a function gives the direction in which the return value will change when each input value changes.

Since the shoot_distance function has three input parameters, the gradient of shoot_distance will return a 3-element Array: one direction for each input parameter.

Thanks to automatic differentiation and the Julia package ForwardDiff.jl gradients can be calculated easily.

Melissa uses the gradient function of ForwardDiff.jl to get the direction in which she needs to change the parameters to make the largest difference.

Do you remember?

What does Melissa need to write into the REPL to install the package ForwardDiff?

] install ForwardDiff
add ForwardDiff
] add ForwardDiff.jl
] add ForwardDiff

Show me the solution

The correct solution is 4: ] to enter pkg mode, then

JULIA

pkg> add ForwardDiff

JULIA

using ForwardDiff: gradient


imprecise_trebuchet = Trebuchet(500.0, 0.25pi);
environment = Environment(5.0, 100.0);

grad = gradient(x ->(shoot_distance([environment.wind, x[2], x[1]])
                      - environment.target_distance),
                imprecise_trebuchet)

OUTPUT

2-element Vector{Float64}:
  -0.12516519503998055
 -49.443442438172205

Melissa now changes her arguments a little bit in the direction of the gradient and checks the new distance.

JULIA

better_trebuchet = imprecise_trebuchet - 0.05 * grad;

shoot_distance([5, better_trebuchet[2], better_trebuchet[1]])

OUTPUT

-2.785549535224487

Great! That didn’t shoot past the target, but instead it landed a bit too short.

Experiment

How far can you change the parameters in the direction of the gradient, such that it still improves the distance?

Try a bunch of values!

JULIA

better_trebuchet = imprecise_trebuchet - 0.04 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
120.48753521261001

JULIA

better_trebuchet = imprecise_trebuchet - 0.03 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
107.80646596787481

JULIA

better_trebuchet = imprecise_trebuchet - 0.02 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
33.90699307740854

JULIA

better_trebuchet = imprecise_trebuchet - 0.025 * grad
shoot_distance([environment.wind, better_trebuchet[2], better_trebuchet[1]])
75.87613276409223

Looks like the “best” trebuchet for a target 100 m away will be between 2.5% and 3% down the gradient from the imprecise trebuchet.

For loops

Now that Melissa knows it is going in the right direction she wants to automate the additional iterations. She writes a new function aim, that performs the application of the gradient N times.

JULIA

function aim(trebuchet, environment; N = 5, η = 0.05)
           better_trebuchet = copy(trebuchet)
           for _ in 1:N
               grad = gradient(x -> (shoot_distance([environment.wind, x[2], x[1]])
                                     - environment.target_distance),
                               better_trebuchet)
               better_trebuchet -= η * grad
           end
           return Trebuchet(better_trebuchet[1], better_trebuchet[2])
       end

better_trebuchet  = aim(imprecise_trebuchet, environment);

shoot_distance(environment.wind, better_trebuchet[2], better_trebuchet[1])

OUTPUT

-2.2195176928658915

Explore

Play around with different inputs of N and η. How close can you come?

Show me the solution

This is a highly non-linear system and thus very sensitive. The distances across different values for the counterweight and the release angle α look like this: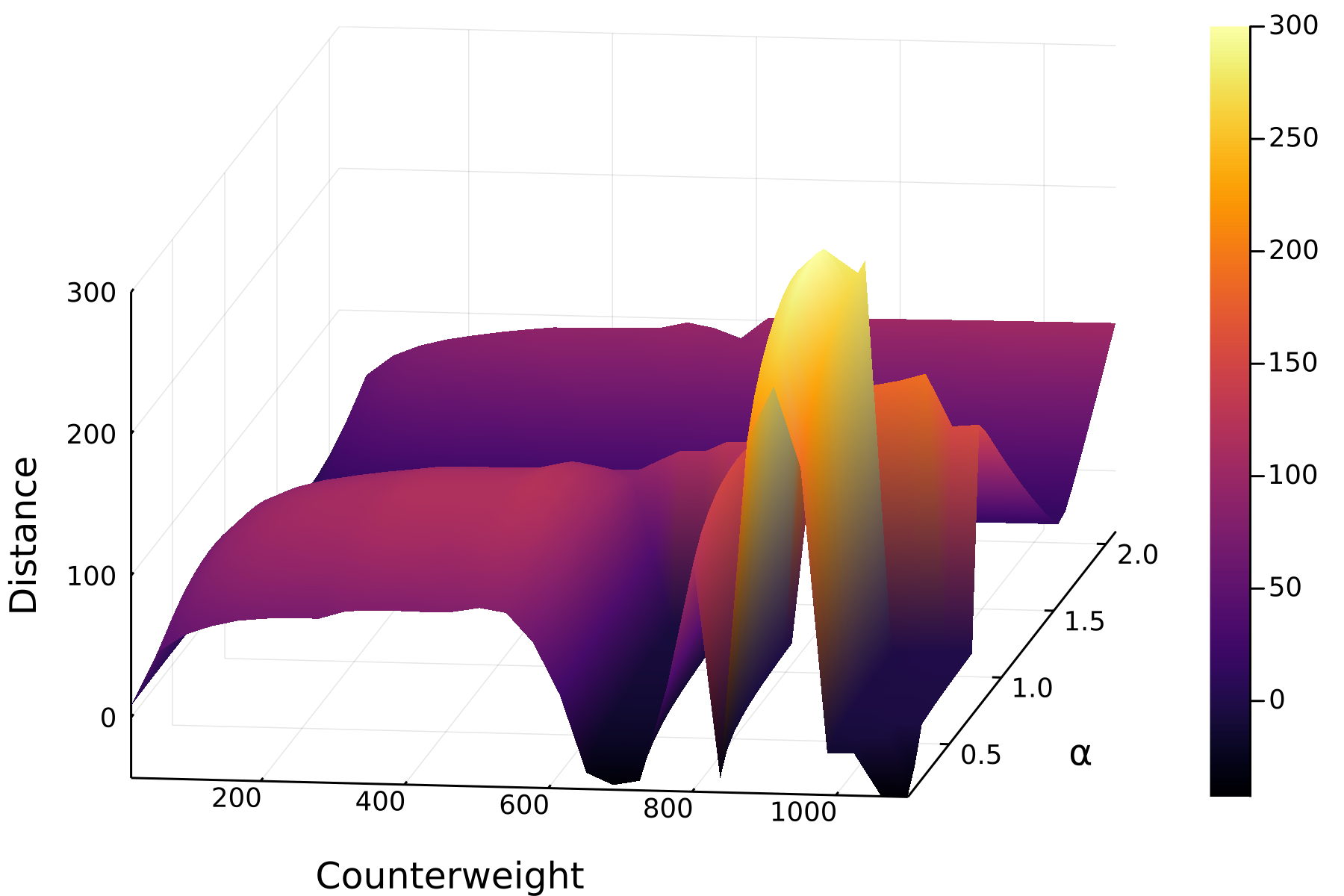

Aborting programs

If a call takes too long, you can abort it with Ctrl-c

While loops

Melissa finds the output of the above aim function too unpredictable to be useful. That’s why she decides to change it a bit. This time she uses a while-loop to run the iterations until she is sufficiently near her target.

(Hint: ε is \epsilontab, and η is \etatab.)

JULIA

function aim(trebuchet, environment; ε = 0.1, η = 0.05)
    better_trebuchet = copy(trebuchet)
    hit = x -> (shoot_distance([environment.wind, x[2], x[1]])
                          - environment.target_distance)
            while abs(hit(better_trebuchet)) > ε
                grad = gradient(hit, better_trebuchet)
                better_trebuchet -= η * grad
            end
            return Trebuchet(better_trebuchet[1], better_trebuchet[2])
        end

better_trebuchet = aim(imprecise_trebuchet, environment);

shoot_distance(better_trebuchet, environment)

OUTPUT

100.05601729579894

That is more what she had in mind. Your trebuchet may be tuned differently, but it should hit just as close as hers.

Key Points

“Use for loops for a known number of iterations and while loops for an unknown number of iterations.”