Content from Introduction
Last updated on 2025-03-31 | Edit this page
Estimated time: 25 minutes
Overview
Questions
- What problems are we solving, and what are we not discussing?
- Why do we use Python?
- What is parallel programming?
- Why can writing a parallel program be challenging?
Objectives
- Recognize serial and parallel patterns.
- Identify problems that can be parallelized.
- Understand a dependency diagram.
Common problems
What problems are we solving?
Ask around what problems participants encountered: “Why did you sign up?” Specifically: “Which task in your field of expertise do you want to parallelize?”
Most problems will fit in either category: - I wrote this code in Python and it is not fast enough. - I run this code on my laptop, but the target size of the problem is bigger than its RAM.
In this course we show several ways of speeding up your program and making it run in parallel. We introduce the following modules:
-
threadingallows different parts of your program to run concurrently on a single computer (with shared memory). -
daskmakes scalable parallel computing easy. -
numbaspeeds up your Python functions by translating them to optimized machine code. -
memory_profilemonitors memory performance. -
asynciois Python’s native asynchronous programming.
FIXME: Actually explain functional programming and distributed programming. More importantly, we show how to change the design of a program to fit parallel paradigms. This often involves techniques from functional programming.
What we won’t talk about
In this course we will not talk about distributed programming. This is a huge can of worms. It is easy to show simple examples, but solutions for particular problems will be wildly different. Dask has a lot of functionalities to help you set up runs on a network. The important bit is that, once you have made your code suitable for parallel computing, you will have the right mindset to get it to work in a distributed environment.
Overview and rationale
FIXME: update this to newer lesson content organisation.
This is an advanced course. Why is it advanced? We (hopefully) saw in the discussion that, although many of your problems share similar characteristics, the details will determine the solution. We all need our algorithms, models, analysis to run so that many hands make light work. When such a situation arises in a group of people, we start with a meeting discussing who does what, when do we meet again and sync up, and so on. After a while you can get the feeling that all you do is to be in meetings. We will see that several abstractions can make our life easier. This course illustrates these abstractions making ample use of Dask.
- Vectorized instructions: tell many workers to do the same work on a
different piece of data. This is where
dask.arrayanddask.dataframecome in. We illustrate this model of working by computing the number \(\pi\) later on. - Map/filter/reduce: this methodology combines different functionals
to create a larger program. We implement this formalism when using
dask.bagto count the number of unique words in a novel. - Task-based parallelization: this may be the most generic
abstraction, as all the others can be expressed in terms of tasks or
workflows. This is
dask.delayed.
Why Python?
Python is one of most widely used languages for scientific data analysis, visualization, and even modelling and simulation. The popularity of Python is mainly due to the two pillars of the friendly syntax and the availability of many high-quality libraries.
It’s not all good news
The flexibility of Python comes with a few downsides, though: - Python code typically does not perform as fast as lower-level implementations in C/C++ or Fortran. - Parallelizing Python code to work efficiently on many-core architectures is not trivial.
This workshop addresses both issues, with an emphasis on running parallel Python code efficiently on multiple cores.
What is parallel computing?
Dependency diagrams
Suppose we have a computation where each step depends on a previous one. We can represent this situation in the schematic below, known as a dependency diagram:

In these diagrams rectangles represent the inputs and outputs of each function. The inward and outward arrows indicate their flow. Note that the output of one function can become the input of another one. The diagram above is the typical diagram of a serial computation. If you ever used a loop to update a value, you used serial computation.
If our computation involves independent work (that is, the results of each function are independent of the results of applying the rest), we can structure our computation as follows:
This scheme represents a parallel computation.
How can parallel computing improve our code execution speed?
Nowadays, most personal computers have 4 or 8 processors (also known as cores). In the diagram above, we can assign each of the three functions to one core, so they can be performed simultaneously.
Do eight processors work eight as fast as one?
It may be tempting to think that using eight cores instead of one would increase the execution speed eightfold. For now, it is OK to use this as a first approximation to reality. Later in the course we see that things are actually more complicated.
Parallelizable and non-parallelizable tasks
Some tasks are easily parallelizable while others are not so inherently. However, it might not always be immediately apparent that a task is parallelizable.
Let us consider the following piece of code:
PYTHON
x = [1, 2, 3, 4] # Write input
y = 0 # Initialize output
for i in range(len(x)):
y += x[i] # Add each element to the output variable
print(y) # Print outputOUTPUT
10Note that each successive loop uses the result of the previous loop. In that way, it depends on the previous loop. The following dependency diagram makes that clear:
Although we are performing the loops in a serial way in the snippet above, nothing prevents us from performing this calculation in parallel. The following example shows that parts of the computations can be done independently:
PYTHON
x = [1, 2, 3, 4]
chunk1 = x[:2]
chunk2 = x[2:]
sum_1 = sum(chunk1)
sum_2 = sum(chunk2)
result = sum_1 + sum_2
print(result)OUTPUT
10Chunking is the technique for parallelizing operations like these sums.
There is a subclass of algorithms where the subtasks are completely independent. These kinds of algorithms are known as embarrassingly parallel or, more friendly, naturally or delightfully parallel.
An example of this kind of problem is squaring each element in a list, which can be done as follows:
Each task of squaring a number is independent of all other elements in the list.
It is important to know that some tasks are fundamentally
non-parallelizable. An example of such an inherently
serial algorithm is the computation of the Fibonacci sequence
using the formula Fn=Fn-1 + Fn-2. Each output depends on
the outputs of the two previous loops.
Challenge: Parallellizable and non-parallellizable tasks
Can you think of a task in your domain that is parallelizable? Can you also think of one that is fundamentally non-parallelizable?
Please write your answers in the collaborative document.
Answers may vary. An ubiquitous example of a naturally parallel problem is a parameter scan, where you need to evaluate some model for N different configurations of input parameters.
Time-dependent models are a category of problems very hard to parallelize, since every state depends on the previous one(s). The attempts to parallelize those cases require fundamentally different algorithms.
In many cases fully paralellizable algorithms may be a bit less efficient per CPU cycle than their single threaded brethren.
Problems versus Algorithms
Often, the parallelizability of a problem depends on its specific implementation. For instance, in our first example of a non-parallelizable task, we mentioned the calculation of the Fibonacci sequence. Conveniently, a closed form expression to compute the n-th Fibonacci number exists.
Last but not least, do not let the name discourage you: if your algorithm happens to be embarrassingly parallel, that’s good news! The adverb “embarrassingly” evokes the feeling of “this is great!, how did I not notice before?!”
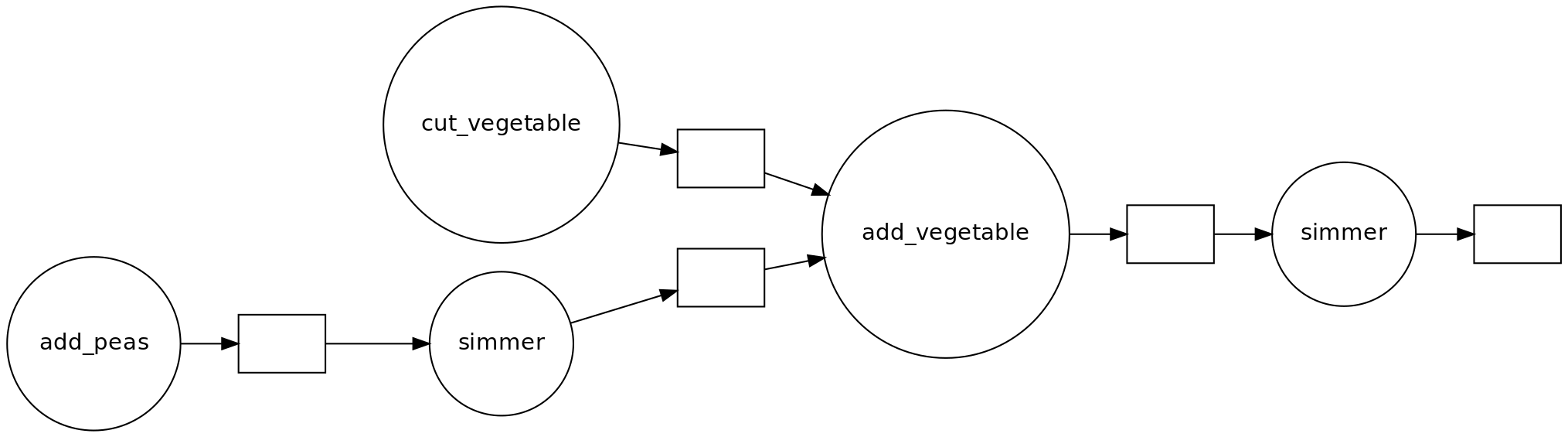
Challenge: Parallelized Pea Soup
We have the following recipe:
- (1 min) Pour water into a soup pan, add the split peas and bay leaf, and bring it to boil.
- (60 min) Remove any foam using a skimmer, and let it simmer under a lid for about 60 minutes.
- (15 min) Clean and chop the leek, celeriac, onion, carrot and potato.
- (20 min) Remove the bay leaf, add the vegetables, and simmer for 20 more minutes. Stir the soup occasionally.
- (1 day) Leave the soup for one day. Re-heat before serving and add a sliced smoked sausage (vegetarian options are also welcome). Season with pepper and salt.
Imagine you are cooking alone.
- Can you identify potential for parallelisation in this recipe?
- And what if you are cooking with a friend’s help? Is the soup done any faster?
- Draw a dependency diagram.
- You can cut vegetables while simmering the split peas.
- If you have help, you can parallelize cutting vegetables further.
- There are two ‘workers’: the cook and the stove.
Shared vs. distributed memory
FIXME: add text
- Programs are parallelizable if you can identify independent tasks.
- To make programs scalable, you need to chunk the work.
- Parallel programming often triggers a redesign; we use different patterns.
- Doing work in parallel does not always give a speed-up.
Content from Benchmarking
Last updated on 2025-03-31 | Edit this page
Estimated time: 60 minutes
Overview
Questions
- How do we know whether our program ran faster in parallel?
- How do we appraise efficiency?
Objectives
- View performance on system monitor.
- Find out how many cores your machine has.
- Use
%timeand%timeitline-magic. - Use a memory profiler.
- Plot performance against number of work units.
- Understand the influence of hyper-threading on timings.
A first example with Dask
We will create parallel programs in Python later. First let’s see a small example. Open your System Monitor (the application will vary between specific operating systems), and run the following code examples:
PYTHON
# The same summation, but using dask to parallelize the code.
# NB: the API for dask arrays mimics that of numpy
import dask.array as da
work = da.arange(10**7).sum()
result = work.compute()Try a heavy enough task
Your system monitor may not detect so small a task. In your computer
you may have to gradually raise the problem size to 10**8
or 10**9 to observe the effect in long enough a run. But be
careful and increase slowly! Asking for too much memory can make your
computer slow to a crawl.
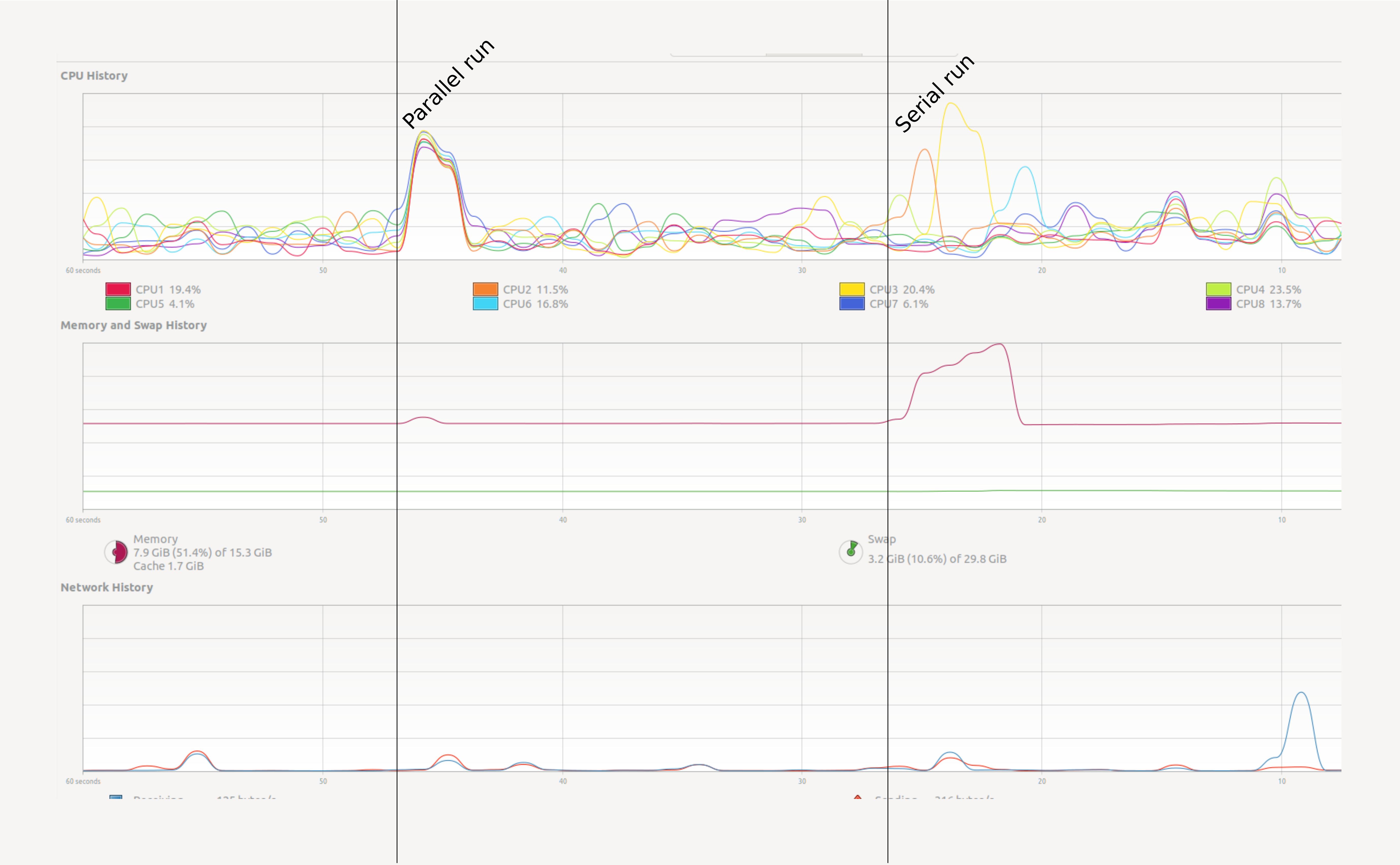
How can we monitor this more conveniently? In Jupyter we can use some
line magics, small “magic words” preceded by the symbol %%
that modify the behaviour of the cell.
The %%time line magic checks how long it took for a
computation to finish. It does not affect how the computation is
performed. In this regard it is very similar to the time
shell command.
If we run the chunk several times, we will notice variability in the
reported times. How can we trust this timer, then? A possible solution
will be to time the chunk several times, and take the average time as
our valid measure. The %%timeit line magic does exactly
this in a concise and convenient manner! %%timeit first
measures how long it takes to run a command once, then repeats it enough
times to get an average run-time. Also, %%timeit can
measure run times discounting the overhead of setting up a problem and
measuring only the performance of the code in the cell. So this outcome
is more trustworthy.
You can store the output of %%timeit in a Python
variable using the -o flag:
Note that this metric does not tell you anything about memory consumption or efficiency.
Python’s map function is lazy. It won’t compute anything
until you iterate it. Try list(map(...)). The third example
doesn’t allocate any memory, which makes it faster.
Memory profiling
- Benchmarking is the action of systematically testing performance under different conditions.
- Profiling is the analysis of which parts of a program contribute to the total performance, and the identification of possible bottlenecks.
We will use the package memory_profiler
to track memory usage. It can be installed executing the code below in
the console:
The memory usage of the serial and parallel versions of a code will
vary. In Jupyter, type the following lines to see the effect in the code
presented above (again, increase the baseline value 10**7
if needed):
PYTHON
import numpy as np
import dask.array as da
from memory_profiler import memory_usage
import matplotlib.pyplot as plt
def sum_with_numpy():
# Serial implementation
np.arange(10**7).sum()
def sum_with_dask():
# Parallel implementation
work = da.arange(10**7).sum()
work.compute()
memory_numpy = memory_usage(sum_with_numpy, interval=0.01)
memory_dask = memory_usage(sum_with_dask, interval=0.01)
# Plot results
plt.plot(memory_numpy, label='numpy')
plt.plot(memory_dask, label='dask')
plt.xlabel('Interval counter [-]')
plt.ylabel('Memory usage [MiB]')
plt.legend()
plt.show()The plot should be similar to the one below:
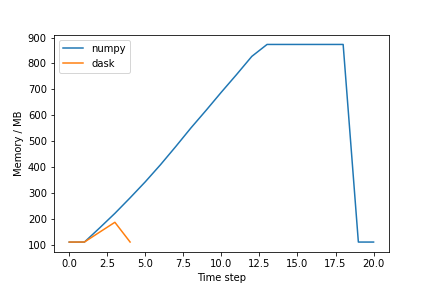
Exercise (plenary)
Why is the Dask solution more memory-efficient?
Chunking! Dask chunks the large array so that the data is never entirely in memory.
Profiling from Dask
Dask has several built-in option for profiling. See the dask documentation for more information.
Using many cores
Using more cores for a computation can decrease the run time. The first question is of course: how many cores do I have? See the snippet below to find this out:
Find out the number of cores in your machine
Usually the number of logical cores is higher than the number of physical cores. This is due to hyper-threading, which enables each physical CPU core to execute several threads at the same time. Even with simple examples, performance may scale unexpectedly. There are many reasons for this, hyper-threading being one of them. See the ensuing example.
On a machine with 4 physical and 8 logical cores, this admittedly over-simplistic benchmark:
PYTHON
x = []
for n in range(1, 9):
time_taken = %timeit -r 1 -o da.arange(5*10**7).sum().compute(num_workers=n)
x.append(time_taken.average)gives the result:
PYTHON
import pandas as pd
data = pd.DataFrame({"n": range(1, 9), "t": x})
data.set_index("n").plot()Discussion
Why does the runtime increase if we add more than 4 cores? This has to do with hyper-threading. On most architectures it does not make much sense to use more workers than the physical cores you have.
- Understanding performance is often non-trivial.
- Memory is just as important as speed.
- To measure is to know.
Content from Computing $\pi$
Last updated on 2025-03-31 | Edit this page
Estimated time: 90 minutes
Overview
Questions
- How do I parallelize a Python application?
- What is data parallelism?
- What is task parallelism?
Objectives
- Rewrite a program in a vectorized form.
- Understand the difference between data-based and task-based parallel programming.
- Apply
numba.jitto accelerate Python.
Parallelizing a Python application
In order to recognize the advantages of parallelism we need an algorithm that is easy to parallelize, complex enough to take a few seconds of CPU time, understandable, and also interesting not to scare away the interested learner. Estimating the value of number \(\pi\) is a classical problem to demonstrate parallel programming.
The algorithm we present is a classical demonstration of the power of Monte Carlo methods. This is a category of algorithms using random numbers to approximate exact results. This approach is simple and has a straightforward geometrical interpretation.
We can compute the value of \(\pi\) using a random number generator. We count the points falling inside the blue circle M compared to the green square N. The ratio 4M/N then approximates \(\pi\).
Challenge: Implement the algorithm
PYTHON
import random
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / N
%timeit calc_pi(10**6)OUTPUT
676 ms ± 6.39 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)Before we parallelize this program, the inner function must be as
efficient as we can make it. We show two techniques for doing this:
vectorization using numpy, and native code
generation using numba.
We first demonstrate a Numpy version of this algorithm:
PYTHON
import numpy as np
def calc_pi_numpy(N):
# Simulate impact coordinates
pts = np.random.uniform(-1, 1, (2, N))
# Count number of impacts inside the circle
M = np.count_nonzero((pts**2).sum(axis=0) < 1)
return 4 * M / NThis is a vectorized version of the original algorithm. A problem written in a vectorized form becomes amenable to data parallelization, where each single operation is replicated over a large collection of data. Data parallelism contrasts with task parallelism, where different independent procedures are performed in parallel. An example of task parallelism is the pea-soup recipe in the introduction.
This implementation is much faster than the ‘naive’ implementation above:
OUTPUT
25.2 ms ± 1.54 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)Discussion: is this all better?
What is the downside of the vectorized implementation? - It uses more memory. - It is less intuitive. - It is a more monolithic approach, i.e., you cannot break it up in several parts.
Challenge: Daskify
Write calc_pi_dask to make the Numpy version parallel.
Compare its speed and memory performance with the Numpy version. NB:
Remember that the API of dask.array mimics that of the
Numpy.
PYTHON
import dask.array as da
def calc_pi_dask(N):
# Simulate impact coordinates
pts = da.random.uniform(-1, 1, (2, N))
# Count number of impacts inside the circle
M = da.count_nonzero((pts**2).sum(axis=0) < 1)
return 4 * M / N
%timeit calc_pi_dask(10**6).compute()OUTPUT
4.68 ms ± 135 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Using Numba to accelerate Python code
Numba makes it easier to create accelerated functions. You can
activate it with the decorator numba.jit.
PYTHON
import numba
@numba.jit
def sum_range_numba(a):
"""Compute the sum of the numbers in the range [0, a)."""
x = 0
for i in range(a):
x += i
return xLet’s time three versions of the same test. First, native Python iterators:
OUTPUT
190 ms ± 3.26 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)Second, with Numpy:
OUTPUT
17.5 ms ± 138 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Third, with Numba:
OUTPUT
162 ns ± 0.885 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)Numba is hundredfold faster in this case! It gets this speedup with
“just-in-time” compilation (JIT) — that is, compiling the Python
function into machine code just before it is called, as the
@numba.jit decorator indicates. Numba does not support
every Python and Numpy feature, but functions written with a for-loop
with a large number of iterates, like in our
sum_range_numba(), are good candidates.
Just-in-time compilation speedup
The first time you call a function decorated with
@numba.jit, you may see no or little speedup. The function
can then be much faster in subsequent calls. Also, timeit
may throw this warning:
The slowest run took 14.83 times longer than the fastest. This could mean that an intermediate result is being cached.
Why does this happen? On the first call, the JIT compiler needs to compile the function. On subsequent calls, it reuses the function previously compiled. The compiled function can only be reused if the types of its arguments (int, float, and the like) are the same as at the point of compilation.
See this example, where sum_range_numba is timed once
again with a float argument instead of an int:
OUTPUT
CPU times: user 58.3 ms, sys: 3.27 ms, total: 61.6 ms
Wall time: 60.9 ms
CPU times: user 5 µs, sys: 0 ns, total: 5 µs
Wall time: 7.87 µsChallenge: Numbify calc_pi
Create a Numba version of calc_pi. Time it.
Add the @numba.jit decorator to the first ‘naive’
implementation.
PYTHON
@numba.jit
def calc_pi_numba(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / N
%timeit calc_pi_numba(10**6)OUTPUT
13.5 ms ± 634 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)Measuring = knowing
Always profile your code to see which parallelization method works best.
numba.jit is not a magical
command to solve your problems
Accelerating your code with Numba often outperforms other methods, but rewriting code to reap the benefits of Numba is not always trivial.
- Always profile your code to see which parallelization method works best.
- Vectorized algorithms are both a blessing and a curse.
- Numba can help you speed up code.
Content from Threads And Processes
Last updated on 2025-03-31 | Edit this page
Estimated time: 90 minutes
Overview
Questions
- What is the Global Interpreter Lock (GIL)?
- How do I use multiple threads in Python?
Objectives
- Understand the GIL.
- Understand the difference between the
threadingandmultiprocessinglibraries in Python.
Threading
Another possibility of parallelizing code is to use the
threading module. This module is built into Python. We will
use it to estimate \(\pi\) once again
in this section.
An example of using threading to speed up your code is:
PYTHON
%%time
n = 10**7
t1 = Thread(target=calc_pi, args=(n,))
t2 = Thread(target=calc_pi, args=(n,))
t1.start()
t2.start()
t1.join()
t2.join()Discussion: where’s the speed-up?
While mileage may vary, parallelizing calc_pi,
calc_pi_numpy and calc_pi_numba in this way
will not give the theoretical speed-up. calc_pi_numba
should give some speed-up, but nowhere near the ideal scaling
for the number of cores. This is because, at any given time, Python only
allows a single thread to access the interpreter, a feature also known
as the Global Interpreter Lock.
A few words about the Global Interpreter Lock
The Global Interpreter Lock (GIL) is an infamous feature of the Python interpreter. It both guarantees inner thread sanity, making programming in Python safer, and prevents us from using multiple cores from a single Python instance. This becomes an obvious problem when we want to perform parallel computations. Roughly speaking, there are two classes of solutions to circumvent/lift the GIL:
- Run multiple Python instances using
multiprocessing. - Keep important code outside Python using OS operations, C++ extensions, Cython, Numba.
The downside of running multiple Python instances is that we need to
share the program state between different processes. To this end, you
need to serialize objects. Serialization entails converting a Python
object into a stream of bytes that can then be sent to the other process
or, for example, stored to disk. This is typically done using
pickle, json, or similar, and creates a large
overhead. The alternative is to bring parts of our code outside Python.
Numpy has many routines that are largely situated outside of the GIL.
Trying out and profiling your application is the only way to know for
sure.
There are several options to make your own routines not subjected to
the GIL: fortunately, numba makes this very easy.
We can unlock the GIL in Numba code by setting
nogil=True inside the numba.jit decorator:
PYTHON
import random
@numba.jit(nopython=True, nogil=True)
def calc_pi_nogil(N):
M = 0
for i in range(N):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x**2 + y**2 < 1:
M += 1
return 4 * M / NThe nopython argument forces Numba to compile the code
without referencing any Python objects, while the nogil
argument disables the GIL during the execution of the function.
Use nopython=True or
@numba.njit
It is generally good practice to use nopython=True with
@numba.jit to make sure the entire function is running
without referencing Python objects, because that will dramatically slow
down most Numba code. The decorator @numba.njit even has
nopython=True by default.
Now we can run the benchmark again, using calc_pi_nogil
instead of calc_pi.
Exercise: try threading on a Numpy function
Many Numpy functions unlock the GIL. Try and sort two randomly
generated arrays using numpy.sort in parallel.
Multiprocessing
Python also enables parallelisation with multiple processes via the
multiprocessing module. It implements an API that is
superficially similar to threading:
PYTHON
import random
from multiprocessing import Process
# function in plain Python
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return (4 * M / N, N) # result, iterations
if __name__ == '__main__':
n = 10**7
p1 = Process(target=calc_pi, args=(n,))
p2 = Process(target=calc_pi, args=(n,))
p1.start()
p2.start()
p1.join()
p2.join()However, under the hood, processes are very different from threads. A new process is created by generating a fresh “copy” of the Python interpreter that includes all the resources associated to the parent. There are three different ways of doing this (spawn, fork, and forkserver), whose availability depends on the platform. We will use spawn as it is available on all platforms. You can read more about the others in the Python documentation. Since creating a process is resource-intensive, multiprocessing is beneficial under limited circumstances — namely, when the resource utilisation (or runtime) of a function is measureably larger than the overhead of creating a new process.
The non-intrusive and safe way of starting a new process is to
acquire a context and work within that context. This
ensures that your application does not interfere with any other
processes that might be in use:
PYTHON
import multiprocessing as mp
def calc_pi(N):
...
if __name__ == '__main__':
# mp.set_start_method("spawn") # if not using a context
ctx = mp.get_context("spawn")
...Passing objects and sharing state
We can pass objects between processes by using Queues
and Pipes. Multiprocessing queues behave similarly to
regular queues: - FIFO: first in, first out. -
queue_instance.put(<obj>) to add. -
queue_instance.get() to retrieve.
Exercise: reimplement calc_pi to
use a queue to return the result
PYTHON
import multiprocessing as mp
import random
def calc_pi(N, que):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
que.put((4 * M / N, N)) # result, iterations
if __name__ == "__main__":
ctx = mp.get_context("spawn")
que = ctx.Queue()
n = 10**7
p1 = ctx.Process(target=calc_pi, args=(n, que))
p2 = ctx.Process(target=calc_pi, args=(n, que))
p1.start()
p2.start()
for i in range(2):
print(que.get())
p1.join()
p2.join()Process pool
The Pool API provides a pool of worker processes that
can execute tasks. Methods of the Pool object offer various
convenient ways to implement data parallelism in your program. The most
convenient way to create a pool object is with a context manager, either
using the toplevel function multiprocessing.Pool, or by
calling the .Pool() method on the context. With the
Pool object, tasks can be submitted by calling methods like
.apply(), .map(), .starmap(), or
their .*_async() versions.
Exercise: adapt the original exercise to submit tasks to a pool
- Use the original
calc_pifunction (without the queue). - Submit batches of different sample size (different values of
N). - As mentioned earlier, creating a new process entails overheads. Try a wide range of sample sizes and check if the runtime scales in keeping with that claim.
PYTHON
from itertools import repeat
import multiprocessing as mp
import random
from timeit import timeit
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return (4 * M / N, N) # result, iterations
def submit(ctx, N):
with ctx.Pool() as pool:
pool.starmap(calc_pi, repeat((N,), 4))
if __name__ == "__main__":
ctx = mp.get_context("spawn")
for i in (1_000, 100_000, 10_000_000):
res = timeit(lambda: submit(ctx, i), number=5)
print(i, res)- If we want the most efficient parallelism on a single machine, we need to work around the GIL.
- If your code disables the GIL, threading will be more efficient than multiprocessing.
- If your code keeps the GIL, some of your code is still in Python and you are wasting precious compute time!
Content from Delayed Evaluation
Last updated on 2025-03-31 | Edit this page
Estimated time: 12 minutes
Overview
Questions
- What abstractions does Dask offer?
- How can I paralellize existing Python code?
Objectives
- Understand the abstraction of delayed evaluation.
- Use the
visualizemethod to create dependency graphs.
Dask is one of many convenient tools
available for parallelizing Python code. We have seen a basic example of
dask.array in a previous episode. Now, we will focus on the
delayed and bag sub-modules. Dask has other
useful components that we do not cover in this lesson, such as
dataframe and futures.
See an overview below:
| Dask module | Abstraction | Keywords | Covered |
|---|---|---|---|
dask.array |
numpy |
Numerical analysis | ✔️ |
dask.bag |
itertools |
Map-reduce, workflows | ✔️ |
dask.delayed |
functions | Anything that doesn’t fit the above | ✔️ |
dask.dataframe |
pandas |
Generic data analysis | ❌ |
dask.futures |
concurrent.futures |
Control execution, low-level | ❌ |
Dask Delayed
A lot of the functionalities in Dask are based on an important
concept known as delayed evaluation. Hence we go a bit deeper
into dask.delayed.
dask.delayed changes the strategy by which our
computation is evaluated. Normally, you expect that a computer runs
commands when you ask for them, and that you can give the next command
when the current job is complete. With delayed evaluation we do not wait
before formulating the next command. Instead, we create the dependency
graph of our complete computation without actually doing any work. Once
we build the full dependency graph, we can see which jobs can be done in
parallel and have those scheduled to different workers.
To express a computation in this world, we need to handle future objects as if they’re already there. These objects may be referred to as either futures or promises.
Several Python libraries provide slightly different support for working with futures. The main difference between Python futures and Dask-delayed objects is that futures are added to a queue at the point of definition, while delayed objects are silent until you ask to compute. We will refer to such ‘live’ futures as futures proper, and to ‘dead’ futures (including the delayed) as promises.
The delayed decorator builds a dependency graph from
function calls:
A delayed function stores the requested function call
inside a promise. The function is not actually executed
yet, and we get a value promised, which can be computed
later.
We can check that x_p is now a Delayed
value:
OUTPUT
[out]: dask.delayed.DelayedNote on notation
It is good practice to suffix with
_pvariables that are promises. That way you keep track of promises versus immediate values. {: .callout}
Only when we ask to evaluate the computation do we get an output:
OUTPUT
1 + 2 = 3
[out]: 3From Delayed values we can create larger workflows and
visualize them:
Challenge: run the workflow
Given this workflow:
Visualize and compute y_p and z_p
separately. How many times is x_p evaluated?
Now change the workflow:
We pass the not-yet-computed promise x_p to both
y_p and z_p. If you only compute
z_p, how many times do you expect x_p to be
evaluated? Run the workflow to check your answer.
We can also make a promise by directly calling
delayed:
It is now possible to call visualize or
compute methods on x_p.
Decorators
In Python the decorator syntax is equivalent to passing a function through a function adapter, also known as a higher order function or a functional. This adapter can change the behaviour of the function in many ways. The statement
is functionally equivalent to:
We can build new primitives from the ground up. An important function
that is found frequently where non-standard evaluation strategies are
involved is gather. We can implement gather as
follows:
Challenge: understand gather
Can you describe what the gather function does in terms
of lists and promises? Hint: Suppose I have a list of promises, what
does gather enable me to do?
It turns a list of promises into a promise of a list.
This small example shows what gather does:
PYTHON
x_p = gather(*(delayed(add)(n, n) for n in range(10))) # Shorthand for gather(add(1, 1), add(2, 2), ...)
x_p.visualize()
{.output alt=“boxes and arrows”}
Computing the result
gives
OUTPUT
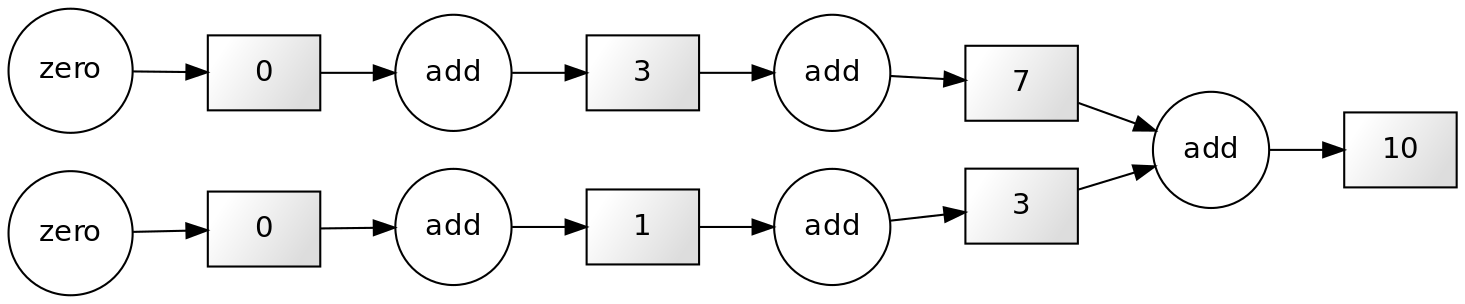
[out]: [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]Challenge: design a mean function
and calculate \(\pi\)
PYTHON
from dask import delayed
import random
@delayed
def mean(*args):
return sum(args) / len(args)
def calc_pi(N):
"""Computes the value of pi using N random samples."""
M = 0
for i in range(N):
# take a sample
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x*x + y*y < 1.: M+=1
return 4 * M / N
N = 10**6
pi_p = mean(*(delayed(calc_pi)(N) for i in range(10)))
pi_p.compute()You may not see a significant speed-up. This is because
dask delayed uses threads by default, and our native Python
implementation of calc_pi does not circumvent the GIL. You
should see a more significant speed-up with the Numba version of
calc_pi, for example.
In practice, you may not need to use @delayed functions
frequently, but they do offer ultimate flexibility. You can build
complex computational workflows in this manner, sometimes replacing
shell scripting, make files, and suchlike.
- We can change the strategy by which a computation is evaluated.
- Nothing is computed until we run
compute(). - With delayed evaluation Dask knows which jobs can be run in parallel.
- Call
computeonly once at the end of your program to get the best results.
Content from Map and Reduce
Last updated on 2025-03-31 | Edit this page
Estimated time: 90 minutes
Overview
Questions
- Which abstractions does Dask offer?
- Which programming patterns exist in the parallel universe?
Objectives
- Recognize
map,filterandreductionpatterns. - Create programs using these building blocks.
- Use the
visualizemethod to create dependency graphs.
In computer science bags are unordered collections of data.
In Dask, a bag is a collection that gets chunked
internally. Operations on a bag are automatically parallelized over the
chunks inside the bag.
Dask bags let you compose functionality using several primitive
patterns: the most important of these are map,
filter, groupby, flatten, and
reduction.
Discussion
Open the Dask
documentation on bags. Discuss the map,
filter, flatten and reduction
methods.
In this set of operations reduction is rather special,
because all operations on bags could be written in terms of a
reduction.
Operations on this level can be distinguished in several categories:
- map (N to N) applies a function one-to-one on a list of arguments. This operation is embarrassingly parallel.
- filter (N to <N) selects a subset from the data.
- reduction (N to 1) computes an aggregate from a sequence of data; if the operation permits it (summing, maximizing, etc), this can be done in parallel by reducing chunks of data and then further processing the results of those chunks.
- groupby (1 bag to N bags) groups data in subcategories.
- flatten (N bags to 1 bag) combine many bags into one.
Let’s see examples of them in action.
First, let’s create the bag containing the elements we
want to work with. In this case, the numbers from 0 to 5.
{: .source}
Map
A function squaring its argument is a mapping function that
illustrates the concept of map:
PYTHON
# Create a function for mapping
def f(x):
return x.upper()
# Create the map and compute it
bag.map(f).compute()OUTPUT
out: ['MARY', 'HAD', 'A', 'LITTLE', 'LAMB']We can also visualize the mapping:
Filter
We need a predicate, that is a function returning either true or
false, to illustrate the concept of filter. In this case,
we use a function returning True if the argument contains
the letter ‘a’, and False if it does not.
PYTHON
# Return True if x contains the letter 'a', else False
def pred(x):
return 'a' in x
bag.filter(pred).compute()OUTPUT
[out]: ['mary', 'had', 'a', 'lamb']Difference between filter and
map
Forecast the output of bag.map(pred).compute() without
executing it.
The output will be [True, True, True, False, True].
Reduction
PYTHON
def count_chars(x):
per_word = [len(w) for w in x]
return sum(per_word)
bag.reduction(count_chars, sum).visualize()Challenge: consider pluck
We previously discussed some generic operations on bags. In the
documentation, lookup the pluck method. How would you
implement pluck if it was not there?
Hint: Try pluck on some example data.
FIXME: find replacement for word counting example.
Challenge: Dask version of Pi estimation
Use map and mean functions on Dask bags to
compute \(\pi\).
PYTHON
import dask.bag
from numpy import repeat
import random
def calc_pi(N):
"""Computes the value of pi using N random samples."""
M = 0
for i in range(N):
# take a sample
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x*x + y*y < 1.:
M += 1
return 4 * M / N
bag = dask.bag.from_sequence(repeat(10**7, 24))
shots = bag.map(calc_pi)
estimate = shots.mean()
estimate.compute()Note
By default Dask runs a bag using multiprocessing. This alleviates problems with the GIL, but also entails a larger overhead.
- Use abstractions to keep programs manageable.
Content from Exercise with Fractals
Last updated on 2025-03-31 | Edit this page
Estimated time: 60 minutes
Overview
Questions
- Can we tackle a real problem now?
Objectives
- Create a strategy to parallelize existing code.
- Apply previous lessons.
The Mandelbrot and Julia fractals
This exercise uses Numpy and Matplotlib.
We will be computing the famous Mandelbrot fractal.
Complex numbers
Complex numbers are a special representation of rotations and scalings in the two-dimensional plane. Multiplying two complex numbers is the same as taking a point, rotate it by an angle \(\phi\) and scale it by the absolute value. Multiplying with a number \(z \in \mathbb{C}\) by 1 preserves \(z\). Multiplying a point at \(i = (0, 1)\) (having a positive angle of 90 degrees and absolute value 1), rotates it anti-clockwise by 90 degrees. Then you might see that \(i^2 = (-1, 0)\). The funny thing is that we can treat \(i\) as any ordinary number, and all our algebra still works out. This is actually nothing short of a miracle! We can write a complex number
\[z = x + iy,\]
remember that \(i^2 = -1\), and act as if everything is normal!
The Mandelbrot set is the set of complex numbers \[c \in \mathbb{C}\] for which the iteration
\[z_{n+1} = z_n^2 + c,\]
converges, starting from iteration at \(z_0 = 0\). We can visualize the Mandelbrot set by plotting the number of iterations needed for the absolute value \(|z_n|\) to exceed 2 (for which it can be shown that the iteration always diverges).
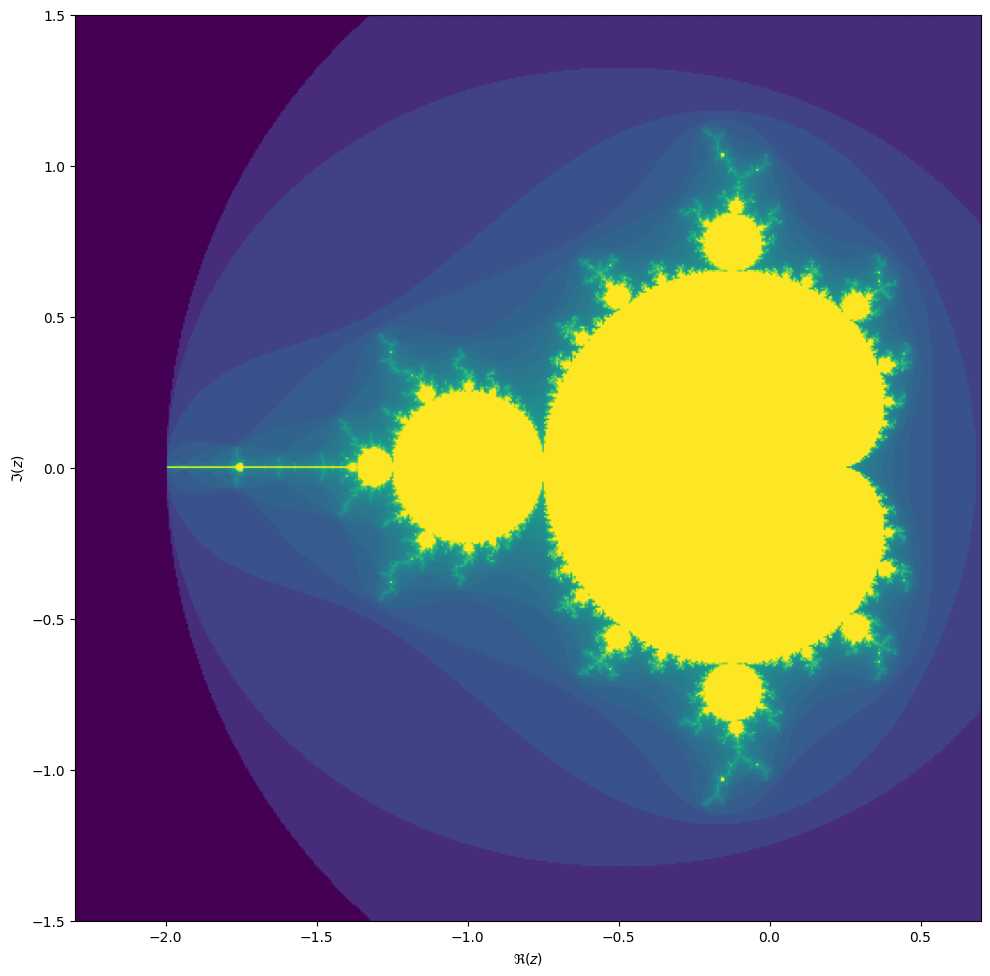
We may compute the Mandelbrot as follows:
PYTHON
max_iter = 256
width = 256
height = 256
center = -0.8 + 0.0j
extent = 3.0 + 3.0j
scale = max((extent / width).real, (extent / height).imag)
result = np.zeros((height, width), int)
for j in range(height):
for i in range(width):
c = center + (i - width // 2 + 1j * (j - height // 2)) * scale
z = 0
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real > 4.0:
break
result[j, i] = kThen we can plot with the following code:
PYTHON
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
plot_extent = (width + 1j * height) * scale
z1 = center - plot_extent / 2
z2 = z1 + plot_extent
ax.imshow(result**(1 / 3), origin='lower', extent=(z1.real, z2.real, z1.imag, z2.imag))
ax.set_xlabel("$\Re(c)$")
ax.set_ylabel("$\Im(c)$")Things become really loads of fun when we zoom in. We can play around
with the center and extent values, and
necessarily max_iter, to control our window:
When we zoom in on the Mandelbrot fractal, we get smaller copies of the larger set!
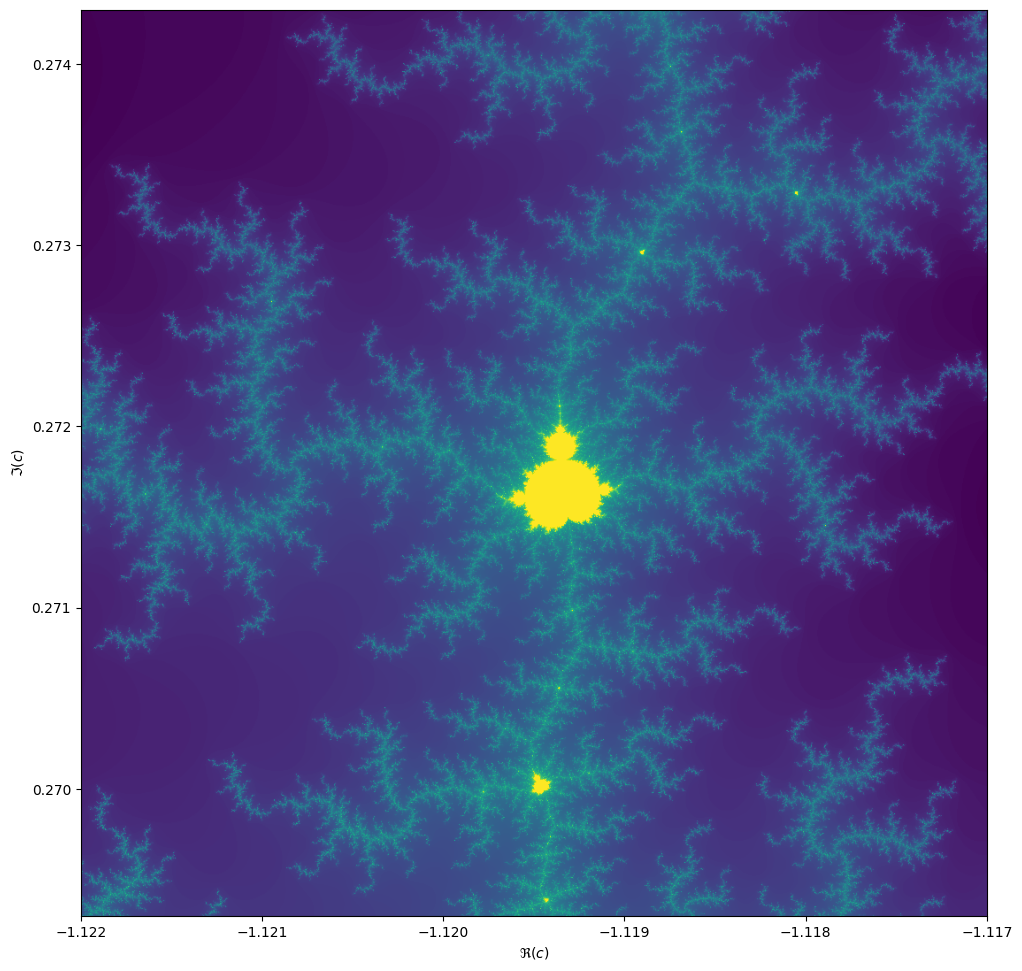
Exercise
Turn this into an efficient parallel program. What kind of speed-ups do you get?
We start with a naive implementation. It may be convenient to define
a BoundingBox class in a separate module
bounding_box.py. We add methods to this class later on.
PYTHON
from dataclasses import dataclass
from typing import Optional
import numpy as np
import dask.array as da
@dataclass
class BoundingBox:
width: int
height: int
center: complex
extent: complex
_scale: Optional[float] = None
@property
def scale(self):
if self._scale is None:
self._scale = max(self.extent.real / self.width,
self.extent.imag / self.height)
return self._scale
<<bounding-box-methods>>
test_case = BoundingBox(1024, 1024, -1.1195+0.2718j, 0.005+0.005j)PYTHON
import matplotlib # type:ignore
matplotlib.use(backend="Agg")
from matplotlib import pyplot as plt
import numpy as np
from bounding_box import BoundingBox
def plot_fractal(box: BoundingBox, values: np.ndarray, ax=None):
if ax is None:
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
else:
fig = None
plot_extent = (box.width + 1j * box.height) * box.scale
z1 = box.center - plot_extent / 2
z2 = z1 + plot_extent
ax.imshow(values, origin='lower', extent=(z1.real, z2.real, z1.imag, z2.imag),
cmap=matplotlib.colormaps["viridis"])
ax.set_xlabel("$\Re(c)$")
ax.set_ylabel("$\Im(c)$")
return fig, axThe natural approach with Python is to speed this up with Numba.
Then, there are three ways to parallelize: first, letting Numba
parallelize the function; second, doing a manual domain decomposition
and using one of the many Python ways to run multi-threaded things;
third, creating a vectorized function and parallelizing it using
dask.array. This last option is almost always slower than
@njit(parallel=True) and domain decomposition.
PYTHON
When we port the core Mandelbrot function to Numba, we need to keep some best practices in mind:
- Don’t pass composite objects other than Numpy arrays.
- Avoid acquiring memory inside a Numba function; rather, create an array in Python and then pass it to the Numba function.
- Write a Pythonic wrapper around the Numba function for easy use.
PYTHON
from typing import Any, Optional
import numba # type:ignore
import numpy as np
from bounding_box import BoundingBox
@numba.njit(nogil=True)
def compute_mandelbrot_numba(
result, width: int, height: int, center: complex,
scale: complex, max_iter: int):
for j in range(height):
for i in range(width):
c = center + (i - width // 2 + 1j * (j - height // 2)) * scale
z = 0.0 + 0.0j
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real >= 4.0:
break
result[j, i] = k
return result
def compute_mandelbrot(
box: BoundingBox, max_iter: int,
result: Optional[np.ndarray[np.int64]] = None,
throttle: Any = None):
result = result if result is not None \
else np.zeros((box.height, box.width), np.int64)
return compute_mandelbrot_numba(
result, box.width, box.height, box.center, box.scale,
max_iter=max_iter)Numba parallel=True
We can parallelize loops directly with Numba. Pass the flag
parallel=True and use prange to create the
loop. Here, it is even more important to obtain the result array outside
the context of Numba, otherwise the result will be slower than the
serial version.
PYTHON
from typing import Optional
import numba # type:ignore
from numba import prange # type:ignore
import numpy as np
from .bounding_box import BoundingBox
@numba.njit(nogil=True, parallel=True)
def compute_mandelbrot_numba(
result, width: int, height: int, center: complex, scale: complex,
max_iter: int):
for j in prange(height):
for i in prange(width):
c = center + (i - width // 2 + (j - height // 2) * 1j) * scale
z = 0.0+0.0j
for k in range(max_iter):
z = z**2 + c
if (z*z.conjugate()).real >= 4.0:
break
result[j, i] = k
return result
def compute_mandelbrot(box: BoundingBox, max_iter: int,
throttle: Optional[int] = None):
if throttle is not None:
numba.set_num_threads(throttle)
result = np.zeros((box.height, box.width), np.int64)
return compute_mandelbrot_numba(
result, box.width, box.height, box.center, box.scale,
max_iter=max_iter)We split the computation into a set of sub-domains. The
BoundingBox.split() method is designed so that, if we
deep-map the resulting list-of-lists, we can recombine the results using
numpy.block().
PYTHON
def split(self, n):
"""Split the domain in nxn subdomains, and return a grid of BoundingBoxes."""
w = self.width // n
h = self.height // n
e = self.scale * w + self.scale * h * 1j
x0 = self.center - e * (n / 2 - 0.5)
return [[BoundingBox(w, h, x0 + i * e.real + j * e.imag * 1j, e)
for i in range(n)]
for j in range(n)]To perform the computation in parallel, let’s go ahead and choose the
most difficult path: asyncio. There are other ways to do
this, like setting up a number of threads or using Dask. However,
asyncio is available in Python natively. In the end, the
result is very similar to what we would get using
dask.delayed.
This may seem as a lot of code, but remember: we only use Numba to compile the core part and then Asyncio to parallelize. The progress bar is a bit of flutter and the semaphore is only there to throttle the computation to fewer cores. Even then, this solution is the most extensive by far but also the fastest.
PYTHON
from typing import Optional
import numpy as np
import asyncio
from psutil import cpu_count # type:ignore
from contextlib import nullcontext
from .bounding_box import BoundingBox
from .numba_serial import compute_mandelbrot as mandelbrot_serial
async def a_compute_mandelbrot(
box: BoundingBox,
max_iter: int,
semaphore: Optional[asyncio.Semaphore]):
async with semaphore or nullcontext():
result = np.zeros((box.height, box.width), np.int64)
await asyncio.to_thread(
mandelbrot_serial, box, max_iter, result=result)
return result
async def a_domain_split(box: BoundingBox, max_iter: int,
sem: Optional[asyncio.Semaphore]):
n_cpus = cpu_count(logical=True)
split = box.split(n_cpus)
split_result = await asyncio.gather(
*(asyncio.gather(
*(a_compute_mandelbrot(b, max_iter, sem)
for b in row))
for row in split))
return np.block(split_result)
def compute_mandelbrot(box: BoundingBox, max_iter: int,
throttle: Optional[int] = None):
sem = asyncio.Semaphore(throttle) if throttle is not None else None
return asyncio.run(a_domain_split(box, max_iter, sem))Another solution is to use Numba’s @guvectorize
decorator. The speed-up (on my machine) is not as dramatic as with the
domain decomposition, though.
PYTHON
def grid(self):
"""Return the complex values on the grid in a 2d array."""
x0 = self.center - self.extent / 2
x1 = self.center + self.extent / 2
g = np.mgrid[x0.imag:x1.imag:self.height*1j,
x0.real:x1.real:self.width*1j]
return g[1] + g[0]*1j
def da_grid(self):
"""Return the complex values on the grid in a 2d array."""
x0 = self.center - self.extent / 2
x1 = self.center + self.extent / 2
x = np.linspace(x0.real, x1.real, self.width, endpoint=False)
y = np.linspace(x0.imag, x1.imag, self.height, endpoint=False)
g = da.meshgrid(x, y)
return g[1] + g[0]*1jPYTHON
from typing import Any
from numba import guvectorize, int64, complex128 # type:ignore
import numpy as np
from .bounding_box import BoundingBox
@guvectorize([(complex128[:, :], int64, int64[:, :])],
"(n,m),()->(n,m)",
nopython=True)
def compute_mandelbrot_numba(inp, max_iter: int, result):
for j in range(inp.shape[0]):
for i in range(inp.shape[1]):
c = inp[j, i]
z = 0.0+0.0j
for k in range(max_iter):
z = z**2 + c
if (z*z.conjugate()).real >= 4.0:
break
result[j, i] = k
def compute_mandelbrot(box: BoundingBox, max_iter: int, throttle: Any = None):
result = np.zeros((box.height, box.width), np.int64)
c = box.grid()
compute_mandelbrot_numba(c, max_iter, result)
return resultPYTHON
from typing import Optional
import timeit
from . import numba_serial, numba_parallel, vectorized, domain_splitting
from .bounding_box import BoundingBox, test_case
compile_box = BoundingBox(16, 16, 0.0+0.0j, 1.0+1.0j)
timing_box = test_case
def compile_run(m):
m.compute_mandelbrot(compile_box, 1)
def timing_run(m, throttle: Optional[int] = None):
m.compute_mandelbrot(timing_box, 1024, throttle=throttle)
modules = ["numba_serial:1", "vectorized:1"] \
+ [f"domain_splitting:{n}" for n in range(1, 9)] \
+ [f"numba_parallel:{n}" for n in range(1, 9)]
if __name__ == "__main__":
with open("timings.txt", "w") as out:
headings = ["name", "n", "min", "mean", "max"]
print(f"{headings[0]:<20}" \
f"{headings[1]:>10}" \
f"{headings[2]:>10}" \
f"{headings[3]:>10}" \
f"{headings[4]:>10}",
file=out)
for mn in modules:
m, n = mn.split(":")
n_cpus = int(n)
setup = f"from mandelbrot.bench_all import timing_run, compile_run\n" \
f"from mandelbrot import {m}\n" \
f"compile_run({m})"
times = timeit.repeat(
stmt=f"timing_run({m}, {n_cpus})",
setup=setup,
number=1,
repeat=50)
print(f"{m:20}" \
f"{n_cpus:>10}" \
f"{min(times):10.5g}" \
f"{sum(times)/len(times):10.5g}" \
f"{max(times):10.5g}",
file=out)
import pandas as pd
from plotnine import ggplot, geom_point, geom_ribbon, geom_line, aes
timings = pd.read_table("timings.txt", delimiter=" +", engine="python")
plot = ggplot(timings, aes(x="n", y="mean", ymin="min", ymax="max",
color="name", fill="name")) \
+ geom_ribbon(alpha=0.3, color="none") \
+ geom_point() + geom_line()
plot.save("mandelbrot-timings.svg")Extra: Julia sets
For each value \[c\] we can compute the Julia set, namely the set of starting values \[z_1\] for which the iteration over \[z_{n+1}=z_n^2 + c\] converges. Every location on the Mandelbrot image corresponds to its own unique Julia set.
PYTHON
max_iter = 256
center = 0.0+0.0j
extent = 4.0+3.0j
scale = max((extent / width).real, (extent / height).imag)
result = np.zeros((height, width), int)
c = -1.1193+0.2718j
for j in range(height):
for i in range(width):
z = center + (i - width // 2 + (j - height // 2)*1j) * scale
for k in range(max_iter):
z = z**2 + c
if (z * z.conjugate()).real > 4.0:
break
result[j, i] = kIf we take the centre of the last image, we get the following rendering of the Julia set:
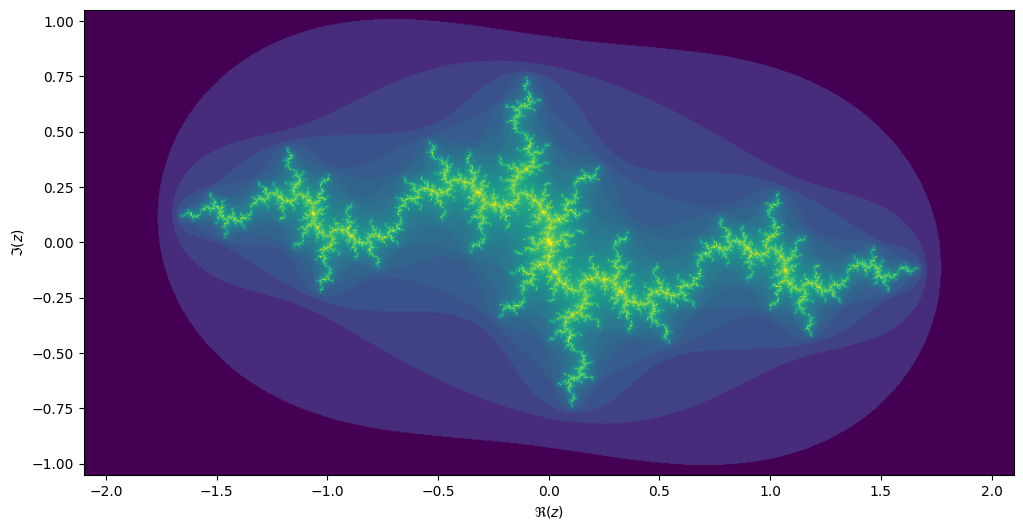
Generalize
Can you generalize your Mandelbrot code to compute both the Mandelbrot and the Julia sets efficiently, while reusing as much code as possible?
- Actually making code faster is not always straightforward.
- Easy one-liners can get you 80% of the way.
- Writing clean and modular code often makes parallelization easier later on.
Content from Asyncio
Last updated on 2025-03-31 | Edit this page
Estimated time: 40 minutes
Overview
Questions
- What is Asyncio?
- When is Asyncio useful?
Objectives
- Understand the difference between a function and a coroutine.
- Know the rudimentary basics of
asyncio. - Perform parallel computations in
asyncio.
Introduction to Asyncio
Asyncio stands for “asynchronous IO” and, as you might have guessed,
has little to do with either asynchronous work or doing IO. In general,
the adjective asynchronous describes objects or events not coordinated
in time. In fact, the asyncio system is more like a set of
gears carefully tuned to run a multitude of tasks as if a lot
of OS threads were running. In the end, they are all powered by the same
crank. The gears in asyncio are called
coroutines and its teeth move other coroutines wherever
you find the await keyword.
The main application for asyncio is hosting back-ends
for web services, where a lot of tasks may be waiting for each other
while the server remains responsive to new events. In that regard,
asyncio is a little bit outside the domain of computational
science. Nevertheless, you may encounter Asyncio code in the wild, and
you can do parallelism with Asyncio if you want higher-level
abstraction without dask or similar alternatives.
Many modern programming languages do have features very similar to
asyncio.
Run-time
The distinctive point of asyncio is a formalism for
carrying out work that is different from usual functions. We need to
look deeper into functions to appreciate the distinction.
Call stacks
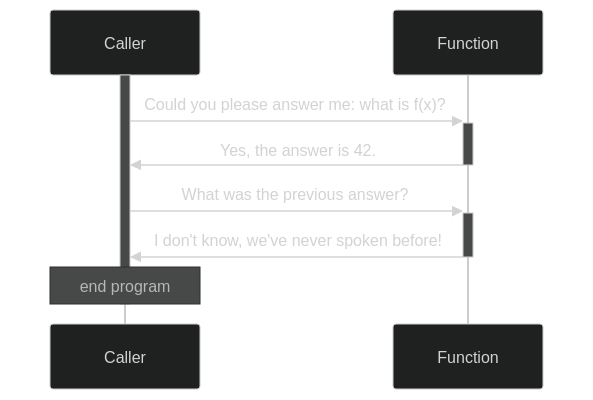
A function call is best understood in terms of a stack-based system. When calling a function, you give it its arguments and temporarily forget what you were doing. Or, rather, you push on a stack and forget whatever you were doing. Then, you start working with the given arguments on a clean sheet (called a stack frame) until you obtain the function result. When you return to the stack, you remember only this result and recall what you originally needed it for. In this manner, every function call pushes a frame onto the stack and every return statement has us popping back to the previous frame.
Mermaid code for above diagram
sequenceDiagram
Caller->>+Function: Could you please answer me: what is f(x)?
Function->>-Caller: Yes, the answer is 42.
Caller->>+Function: What was the previous answer?
Function->>-Caller: I don't know, we've never spoken before!Crucially, when we pop back, we also forget the stack frame inside the function. This way of doing always keeps a single conscious stream of thought. Function calls can be evaluated by a single active agent.
Coroutines
This section goes rather in depth into coroutines. This is meant to
nurture the correct mental model about what goes on with
asyncio.
Working with coroutines changes things a bit. The coroutine keeps on existing and its context is not forgotten when a coroutine returns a result. Python has several forms of coroutines and the simplest is a generator. For example, the following generator produces all integers (if you wait long enough):
Then:
or:
OUTPUT
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]Mermaid code for above diagram
sequenceDiagram
Caller->>+Integers: Please start counting
Caller-->>Integers: What is the next number?
Integers-->>Caller: 1
Caller-->>Integers: What is the next number?
Integers-->>Caller: 2
GC-->>Integers: I'm sorry, you were forgotten about!
Integers->>-GC: Ok, I'll stop existingChallenge: generate all even numbers
Can you write a generator for all even numbers? Reuse
integers(). Extra: Can you generate the Fibonacci
sequence?
The generator gives away control, passing back a value and expecting
to receive control one more time, if faith has it. All meanings of the
keyword yield apply here: the coroutine yields control and
produces a yield, as if we were harvesting a crop.
Conceptually, a generator entails one-way traffic only: we get
output. However, we can use yield also to send information
to a coroutine. For example, this coroutine prints whatever you send to
it:
PYTHON
def printer():
while True:
x = yield
print(x)
p = printer()
next(p) # we need to advance the coroutine to the first yield
p.send("Mercury")
p.send("Venus")
p.send("Earth")Challenge: line numbers
Change printer to add line numbers to the output.
In practice, the send-form of coroutines is hardly ever used. Cases for needing it are infrequent, and chances are that nobody will understand your code. Asyncio has largely superseded this usage.
The working of asyncio is only a small step farther than
that of coroutines. The intuition is to use coroutines to build a
collaborative multi-threading environment. Most modern operating systems
assign some time to execution threads and take back control
pre-emptively to do something else. In collaborative
multi-tasking, every worker knows to be part of a collaborative
environment and yields control to the scheduler voluntarily. Creating
such a system with coroutines and yield is possible in
principle, but is not straightforward especially owing to the
propagation of exceptions.
Syntax
asyncio itself is a library in standard Python and is a
core component for actually using the associated async syntax. Two
keywords are especially relevant here: async and
await.
async is a modifier keyword that makes any subsequent
syntax behave consistently with the asynchronous run-time.
await is used inside a coroutine to wait until another
coroutine yields a result. Effectively, the scheduler takes control
again and may decide to return it when a result is present.
A first program
Jupyter understands asynchronous code, so you can await
futures in any cell:
PYTHON
import asyncio
async def counter(name):
for i in range(5):
print(f"{name:<10} {i:03}")
await asyncio.sleep(0.2)
await counter("Venus")OUTPUT
Venus 000
Venus 001
Venus 002
Venus 003
Venus 004We can have coroutines work concurrently when we gather
them:
OUTPUT
Earth 000
Moon 000
Earth 001
Moon 001
Earth 002
Moon 002
Earth 003
Moon 003
Earth 004
Moon 004
```§
Note that, although the Earth counter and Moon counter seem to operate at the same time, the scheduler is actually alternating them in a single thread! If you work outside of Jupyter, you need an asynchronous main function and must run it using `asyncio.run`. A typical program will look like this:
```python
import asyncio
...
async def main():
...
if __name__ == "__main__":
asyncio.run(main())Asyncio is as contagious as Dask. Any higher-level code must be async
once you have some async low-level code: it’s
turtles all the way down! You may be tempted to implement
asyncio.run in the middle of your code and interact with
the asynchronous parts. Multiple active Asyncio run-times will get you
into troubles, though. Mixing Asyncio and classic code is possible in
principle, but is considered bad practice.
Timing asynchronous code
Jupyter works very well with asyncio except for line
magics and cell magics. We must then write our own timer.
It may be best to have participants copy and paste this snippet from the collaborative document. You may want to explain what a context manager is, but don’t overdo it. This is advanced code and may scare off novices.
PYTHON
from dataclasses import dataclass
from typing import Optional
from time import perf_counter
from contextlib import asynccontextmanager
@dataclass
class Elapsed:
time: Optional[float] = None
@asynccontextmanager
async def timer():
e = Elapsed()
t = perf_counter()
yield e
e.time = perf_counter() - tNow we can write:
OUTPUT
that took 0.20058414503000677 secondsUnderstanding these few snippets of code requires advanced knowledge
of Python. Rest assured that both classic coroutines and
asyncio are complex topics that we cannot cover completely.
However, we can time the execution of our code now!
Compute \(\pi\) again
As a reminder, here is our Numba code for computing \(\pi\):
PYTHON
import random
import numba
@numba.njit(nogil=True)
def calc_pi(N):
M = 0
for i in range(N):
# Simulate impact coordinates
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# True if impact happens inside the circle
if x**2 + y**2 < 1.0:
M += 1
return 4 * M / NWe can send this work to another thread with
asyncio.to_thread:
Gather multiple outcomes
We have already seen that asyncio.gather gathers
multiple coroutines. Here, gather several calc_pi
computations and time them.
We can put this into a new function calc_pi_split:
PYTHON
async def calc_pi_split(N, M):
lst = await asyncio.gather(*(asyncio.to_thread(calc_pi, N) for _ in range(M)))
return sum(lst) / Mand then verify the speed-up that we get:
PYTHON
async with timer() as t:
pi = await asyncio.to_thread(calc_pi, 10**8)
print(f"Value of π: {pi}")
print(f"that took {t.time} seconds")OUTPUT
Value of π: 3.1418552
that took 2.3300534340087324 secondsPYTHON
async with timer() as t:
pi = await calc_pi_split(10**7, 10)
print(f"Value of π: {pi}")
print(f"that took {t.time} seconds")OUTPUT
Value of π: 3.1416366400000006
that took 0.5876454019453377 secondsWorking with asyncio outside Jupyter
Jupyter already has an asynchronous loop running for us. In order to
run scripts outside Jupyter you should write an asynchronous main
function and call it using asyncio.run.
Compute \(\pi\) in a script
Collect in a script what we have done so far to compute \(\pi\) in parallel, and run it.
Ensure that you create an async main function, and run
it using asyncio.run. Create a small module called
calc_pi.
Put the Numba code in a separate file
calc_pi/numba.py.
Put the async_timer function in a separate file
async_timer.py.
PYTHON
# file: calc_pi/async_pi.py
import asyncio
from async_timer import timer
from .numba import calc_pi
<<async-calc-pi>>
async def main():
calc_pi(1)
<<async-calc-pi-main>>
if __name__ == "__main__":
asyncio.run(main())You may run this script using
python -m calc_pi.async_pi.
Efficiency
Play with different subdivisions in calc_pi_split
keeping M*N constant. How much overhead do you see?
PYTHON
import asyncio
import pandas as pd
from plotnine import ggplot, geom_line, geom_point, aes, scale_y_log10, scale_x_log10
from .numba import calc_pi
from .async_pi import calc_pi_split
from async_timer import timer
calc_pi(1) # compile the numba function
async def main():
timings = []
for njobs in [2**i for i in range(13)]:
jobsize = 2**25 // njobs
print(f"{jobsize} - {njobs}")
async with timer() as t:
await calc_pi_split(jobsize, njobs)
timings.append((jobsize, njobs, t.time))
timings = pd.DataFrame(timings, columns=("jobsize", "njobs", "time"))
plot = ggplot(timings, aes(x="njobs", y="time")) \
+ geom_line() + geom_point() + scale_y_log10() + scale_x_log10()
plot.save("asyncio-timings.svg")
if __name__ == "__main__":
asyncio.run(main())The work takes about 0.1 s more when using 1000 tasks. So, assuming that the total overhead is distributed uniformly among the tasks, we observe that the overhead is around 0.1 ms per task.
- Use the
asynckeyword to write asynchronous code. - Use
awaitto call coroutines. - Use
asyncio.gatherto collect work. - Use
asyncio.to_threadto perform CPU intensive tasks. - Inside a script: always create an asynchronous
mainfunction, and run it withasyncio.run.
Content from Calling External C and C++ Libraries from Python
Last updated on 2025-03-31 | Edit this page
Estimated time: 90 minutes
Overview
Questions
- Which options are available to call from Python C and C++ libraries?
- How does this work together with Numpy arrays?
- How do I use this in multiple threads while lifting the GIL?
Objectives
- Compile and link simple C programs into shared libraries.
- Call these libraries from Python and time their executions.
- Compare the performance with Numba-decorated Python code.
- Bypass the GIL when calling these libraries from multiple threads simultaneously.
Calling C and C++ libraries
Simple example using either pybind11 or ctypes
External C and C++ libraries can be called from Python code using a
number of options, e.g., Cython, CFFI, pybind11 and ctypes. We will
discuss the last two because simple cases require the least amount of
boilerplate. This may not be the case with more complex examples.
Consider this simple C program, test.c, which adds up
consecutive numbers:
C
#include <pybind11/pybind11.h>
namespace py = pybind11;
long long sum_range(long long high)
{
long long i;
long long s = 0LL;
for (i = 0LL; i < high; i++)
s += (long long)i;
return s;
}
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "Export the sum_range function as sum_range";
m.def("sum_range", &sum_range, "Adds upp consecutive integer numbers from 0 up to and including high-1");
}You can easily compile and link it into a shared object
(*.so) file with pybind11. You can install
that in several ways, like pip; I prefer creating virtual
environments using pipenv:
BASH
pip install pipenv
pipenv install pybind11
pipenv shell
c++ -O3 -Wall -shared -std=c++11 -fPIC `python3 -m pybind11 --includes` test.c -o test_pybind.sowhich generates a shared object test_pybind.so, which
can be called from a iPython shell as follows:
PYTHON
%import test_pybind
%sum_range=test_pybind.sum_range
%high=1000000000
%brute_force_sum=sum_range(high)Now you might want to check and compare the output with the well-known formula for the sum of consecutive integers:
PYTHON
%sum_from_formula=high*(high-1)//2
%sum_from_formula
%difference=sum_from_formula-brute_force_sum
%differenceGive this script a suitable name, such as
call_C_libraries.py. The same thing can be done using
ctypes instead of pybind11, but the coding
requires slightly more boilerplate on the Python side and slightly less
on the C side. The program test.c will just contain the
algorithm:
C
long long sum_range(long long high)
{
long long i;
long long s = 0LL;
for (i = 0LL; i < high; i++)
s += (long long)i;
return s;
}Compile and link with:
which generates a libtest.so file.
You then need some extra boilerplate:
PYTHON
%import ctypes
%testlib = ctypes.cdll.LoadLibrary("./libtest.so")
%sum_range = testlib.sum_range
%sum_range.argtypes = [ctypes.c_longlong]
%sum_range.restype = ctypes.c_longlong
%high=1000000000
%brute_force_sum=sum_range(high)Again, you can compare the result with the formula for the sum of consecutive integers:
Performance
Now we can time our compiled sum_range C library,
e.g. from the iPython interface:
OUTPUT
2.69 ms ± 6.01 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)If you contrast with the Numba timing in Episode 3, you will see that the C library
for sum_range is faster than the Numpy computation but
significantly slower than the numba.jit-decorated
function.
C versus Numba
Check if the Numba version of this conditional sum range
function outperforms its C counterpart.
Inspired by a blog by Christopher Swenson.
Insert a line if i%3==0: in the code for
sum_range_numba and rename it to
conditional_sum_range_numba:
PYTHON
@numba.jit
def conditional_sum_range_numba(a: int):
x = 0
for i in range(a):
if i%3==0:
x += i
return xLet’s check how fast it runs:
%timeit conditional_sum_range_numba(10**7)OUTPUT
8.11 ms ± 15.6 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)Compare this with the run time of the C code for
conditional_sum_range. Compile and link in the usual way, assuming the
file name is still test.c:
Again, we can time our compiled conditional_sum_range C
library, e.g. from the iPython interface:
PYTHON
import ctypes
testlib = ctypes.cdll.LoadLibrary("./libtest.so")
conditional_sum_range = testlib.conditional_sum_range
conditional_sum_range.argtypes = [ctypes.c_longlong]
conditional_sum_range.restype = ctypes.c_longlong
%timeit conditional_sum_range(10**7)OUTPUT
7.62 ms ± 49.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)The C code is somewhat faster than the Numba-decorated Python code for this slightly more complicated example.
Passing Numpy arrays to C libraries
Now let us consider a more complex example. Instead of computing the
sum of numbers up to an upper limit, let us compute that for an array of
upper limits. This operation will return an array of sums. How difficult
is it to modify our C and Python code to get this done? You just need to
replace &sum_range with
py::vectorize(sum_range):
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", py::vectorize(sum_range), "Adds upp consecutive integer numbers from 0 up to and including high-1");
}Now let’s see what happens if we pass to test_pybind.so
an array instead of an integer.
The code:
gives
OUTPUT
array([ 0, 0, 1, 3, 6, 10, 15, 21, 28, 36])It does not crash! You can check that the array is correct upon subtracting the previous sum from each sum (except the first):
which gives
OUTPUT
array([0, 1, 2, 3, 4, 5, 6, 7, 8])which are the elements of ys except the last, as
expected.
Call the C library from multiple threads simultaneously.
We can show that a C library compiled using pybind11 can
be run as multithreaded. Try the following from an iPython shell:
OUTPUT
274 ms ± 1.03 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)Now try a straightforward parallelization of 20 calls of
sum_range over two threads, hence at 10 calls per thread.
This should take about 10 * 274 ms = 2.74 s for a
parallelization free of overheads. Running:
PYTHON
import threading as T
import time
def timer():
start_time = time.time()
for x in range(10):
t1 = T.Thread(target=sum_range, args=(high,))
t2 = T.Thread(target=sum_range, args=(high,))
t1.start()
t2.start()
t1.join()
t2.join()
end_time = time.time()
print(f"Time elapsed = {end_time-start_time:.2f}s")
timer()gives
Time elapsed = 5.59si.e., more than twice the time we expected. In fact, the
sum_range was run sequentially instead of parallelly. We
then need to add a single declaration to test.c:
py::call_guard<py::gil_scoped_release>():
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", py::vectorize(sum_range), "Adds upp consecutive integer numbers from 0 up to and including high-1");
}as follows:
C
PYBIND11_MODULE(test_pybind, m) {
m.doc() = "pybind11 example plugin"; // optional module docstring
m.def("sum_range", &sum_range, "A function which adds upp numbers from 0 up to and including high-1", py::call_guard<py::gil_scoped_release>());
}Now compile again:
BASH
c++ -O3 -Wall -shared -std=c++11 -fPIC `python3 -m pybind11 --includes` test.c -o test_pybind.soImport again the rebuilt shared object (only possible after quitting and relaunching the iPython interpreter), and time again.
This code:
PYTHON
import test_pybind
import time
import threading as T
sum_range=test_pybind.sum_range
high=int(1e9)
def timer():
start_time = time.time()
for x in range(10):
t1 = T.Thread(target=sum_range, args=(high,))
t2 = T.Thread(target=sum_range, args=(high,))
t1.start()
t2.start()
t1.join()
t2.join()
end_time = time.time()
print(f"Time elapsed = {end_time-start_time:.2f}s")
timer()gives:
OUTPUT
Time elapsed = 2.81sas you would expect for two sum_range modules running in
parallel.
- Multiple options are available to call external C and C++ libraries, and the best choice depends on the complexity of your problem.
- Obviously, there is an extra compile-and-link step, but the execution will be much faster than pure Python.
- Also, the GIL will be circumvented in calling these libraries.
- Numba might also offer you the speed-up you want with even less effort.