Introduction to Diffusion MRI data
Figure 1
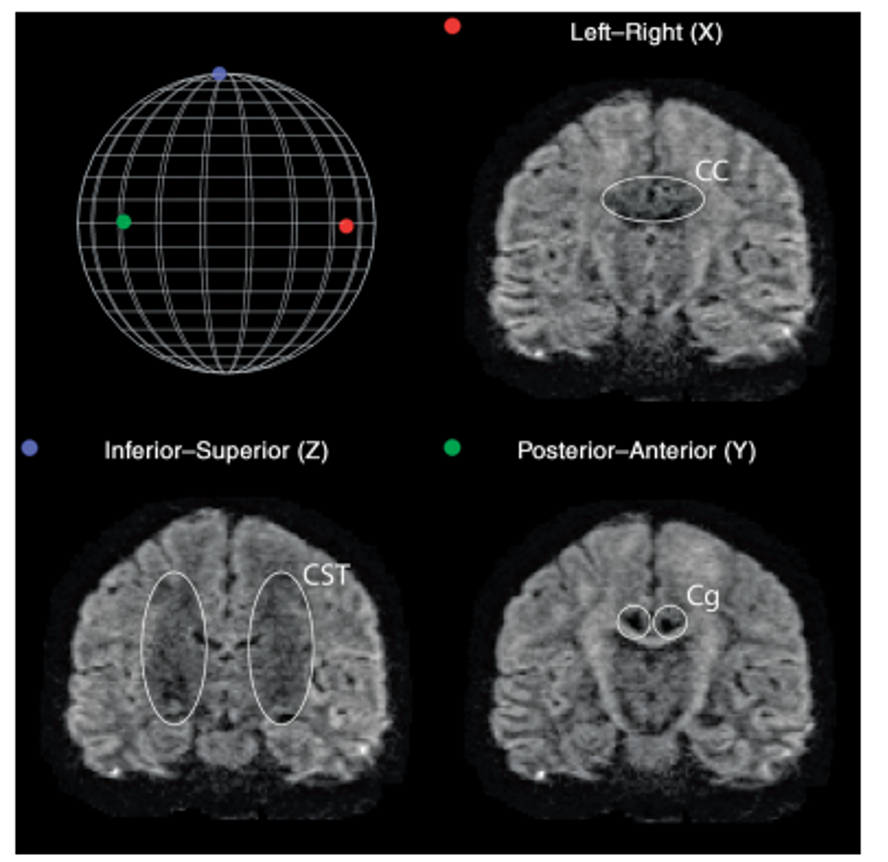
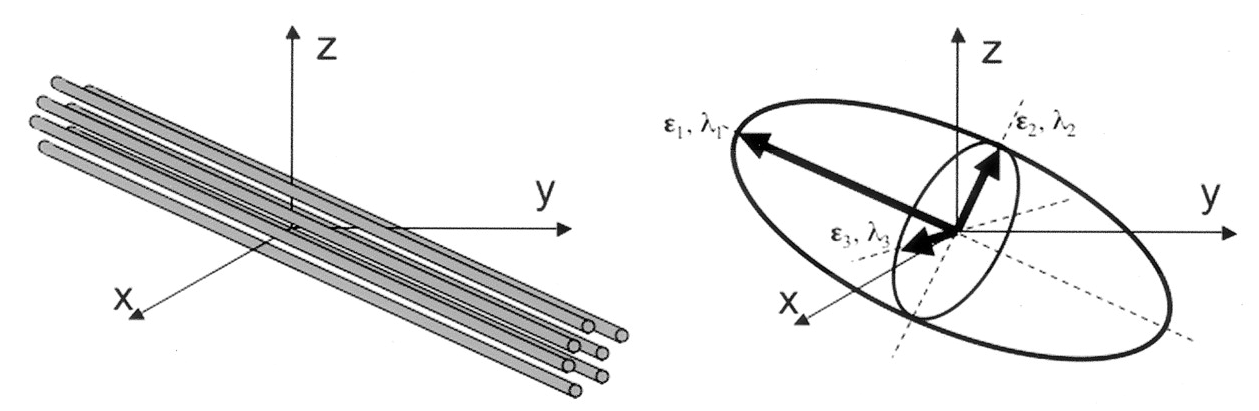
Diffusion along X, Y, and Z directions. The signal in the left/right
oriented corpus callosum is lowest when measured along X, while the
signal in the inferior/superior oriented corticospinal tract is lowest
when measured along Z.
Figure 2
Figure 3
Preprocessing dMRI data
Figure 1
To illustrate what the preprocessing step may look like, here is an
example preprocessing workflow from QSIPrep (Cieslak et al,
2020): 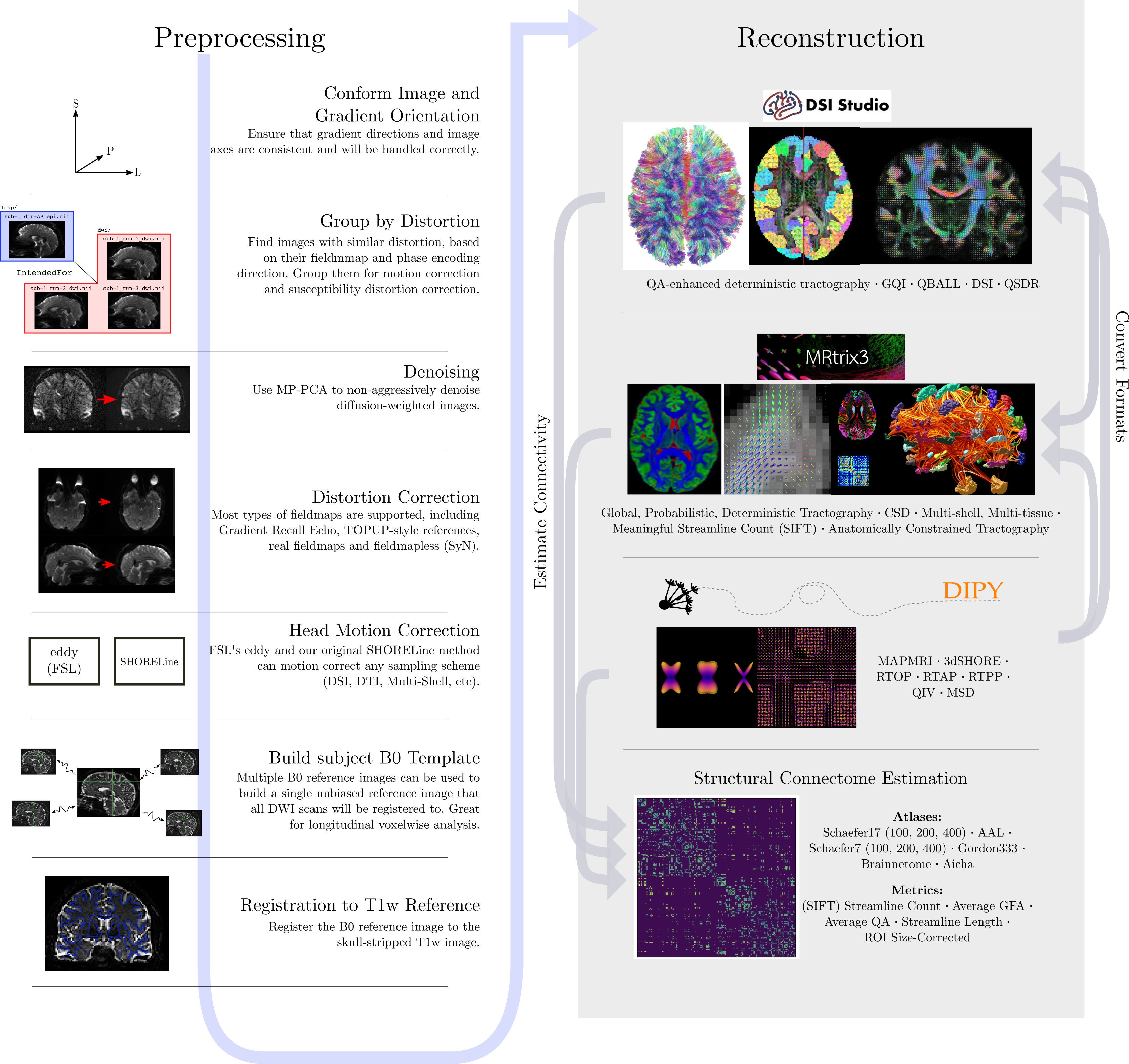
Figure 2
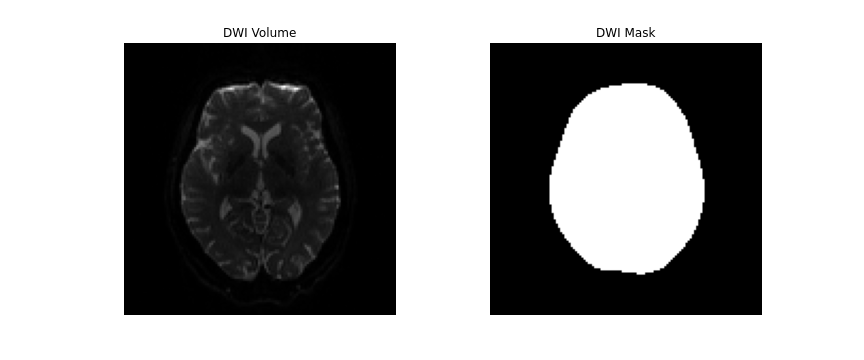
Figure 3
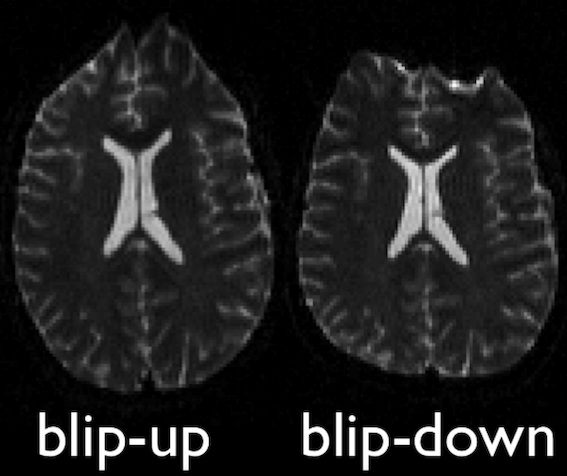
Opposite phase-encodings from two DWI
Figure 4
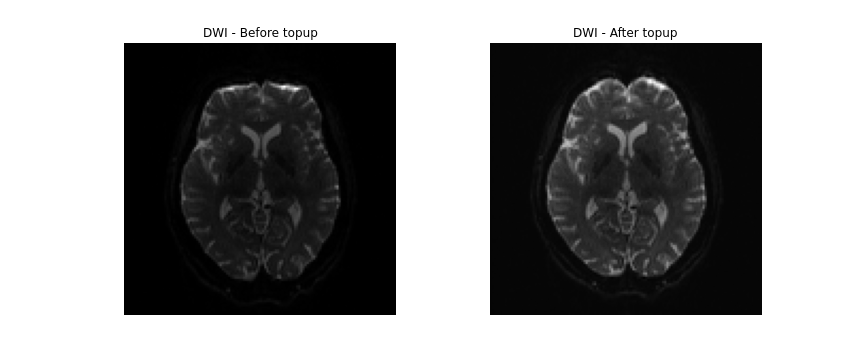
Figure 5
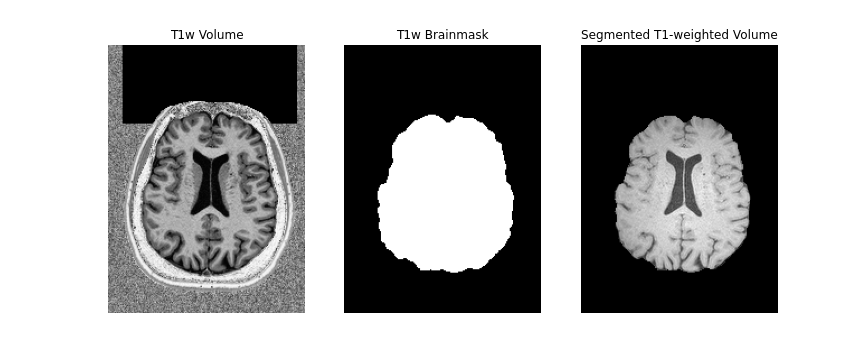
Figure 6
Local fiber orientation reconstruction
Diffusion Tensor Imaging (DTI)
Figure 1
Figure 2
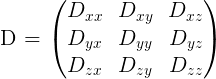
Figure 3
 Adapted from Jelison et al., 2004
Adapted from Jelison et al., 2004
Figure 4
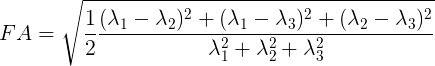
Figure 5
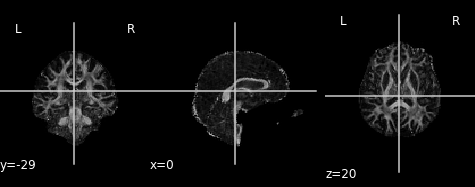
Figure 6
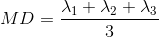
Figure 7
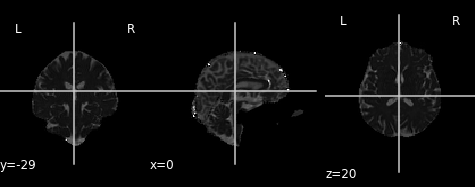
Figure 8
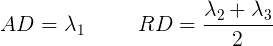
Figure 9
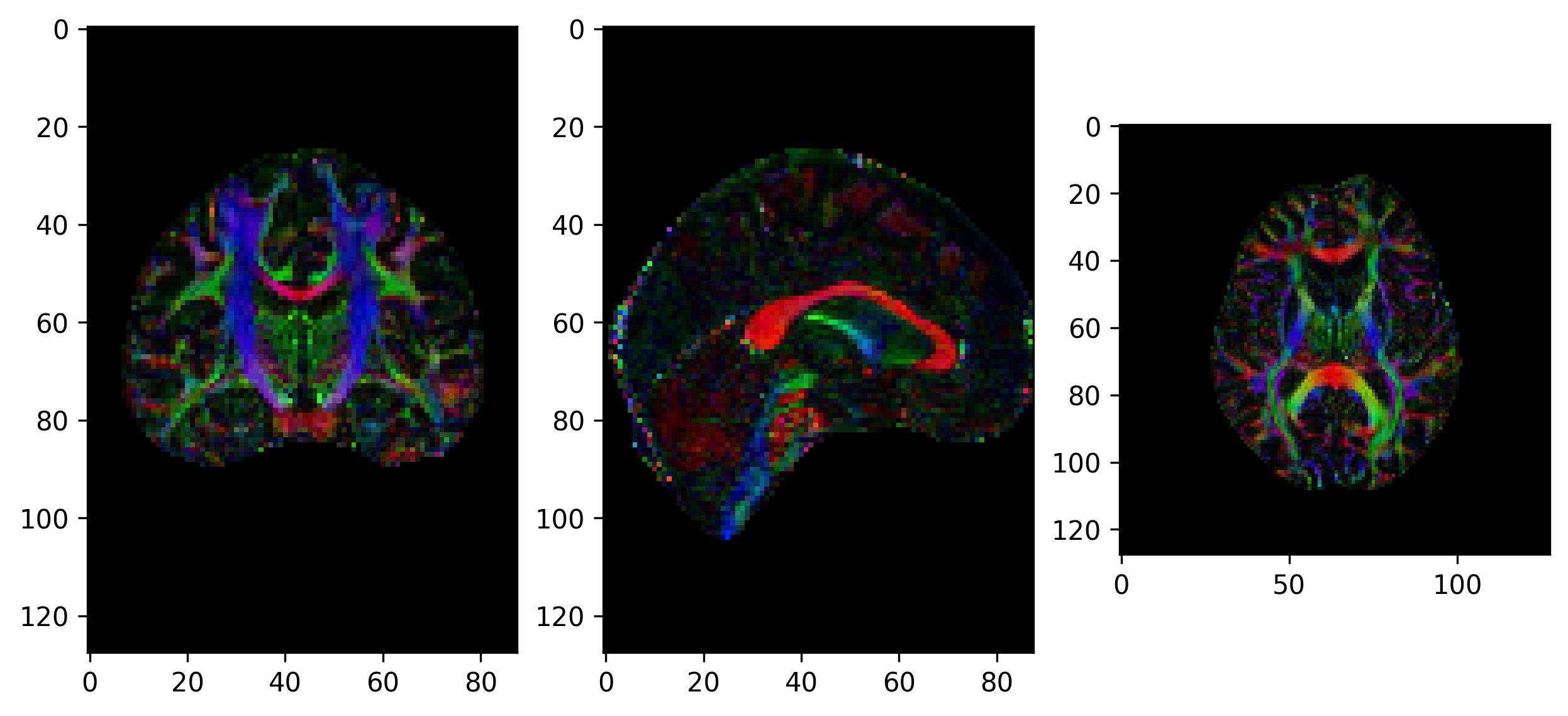
Figure 10
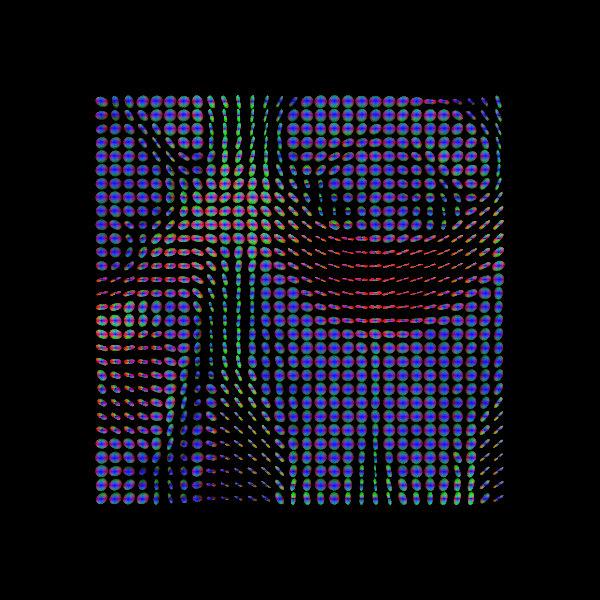
Figure 11
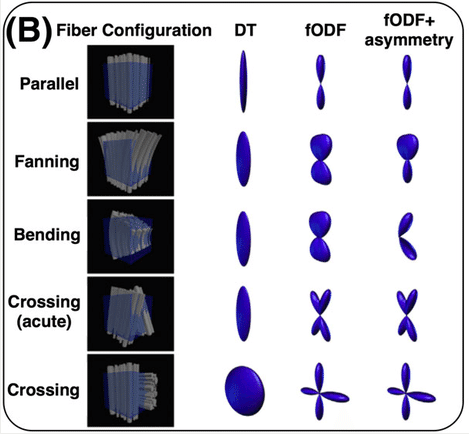
Figure 12
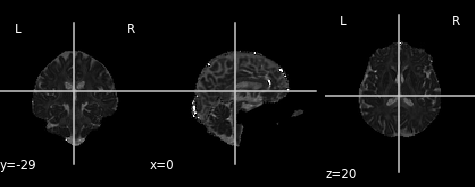
Axial diffusivity map.
Figure 13
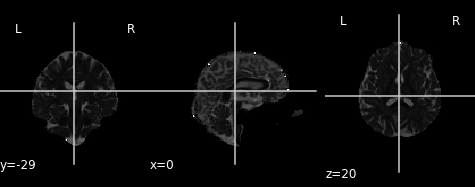
Radial diffusivity map.
Constrained Spherical Deconvolution (CSD)
Figure 1
The basic equations of an SD method can be summarized as 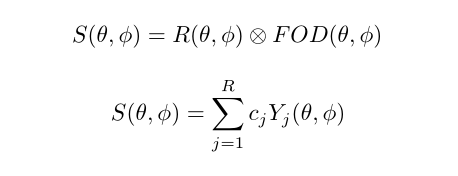
Spherical deconvolution
Figure 2
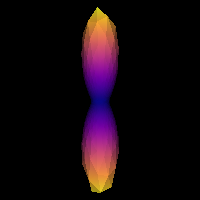
Estimated response function
Figure 3
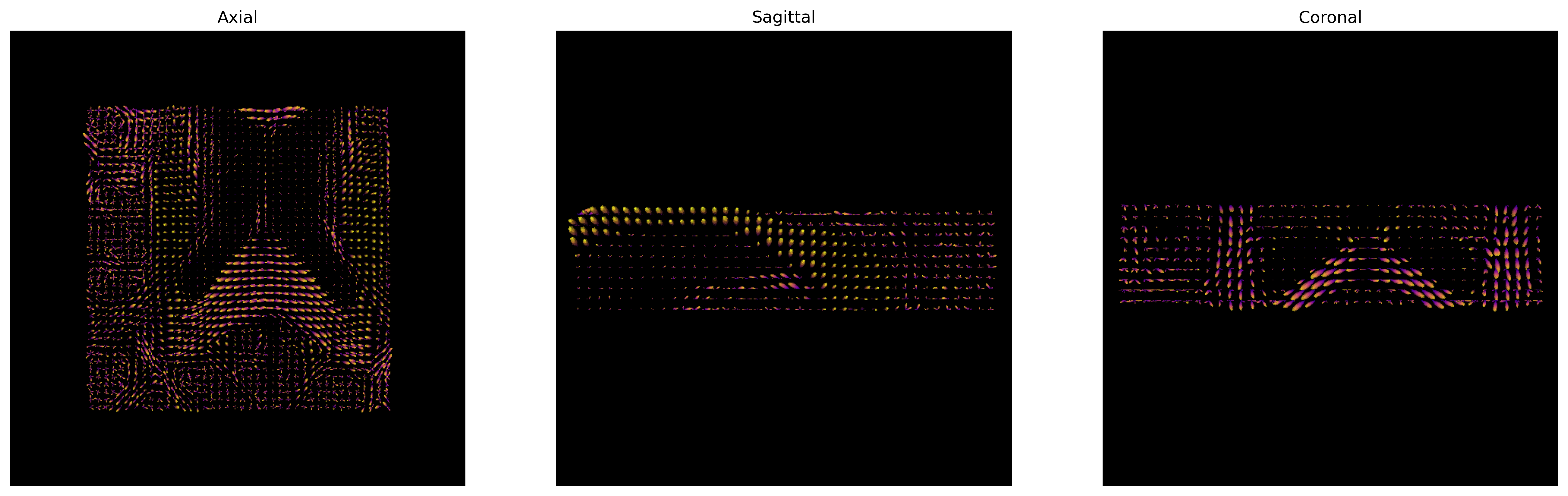
CSD ODFs.
Figure 4

CSD Peaks.
Figure 5

CSD Peaks and ODFs.
Figure 6
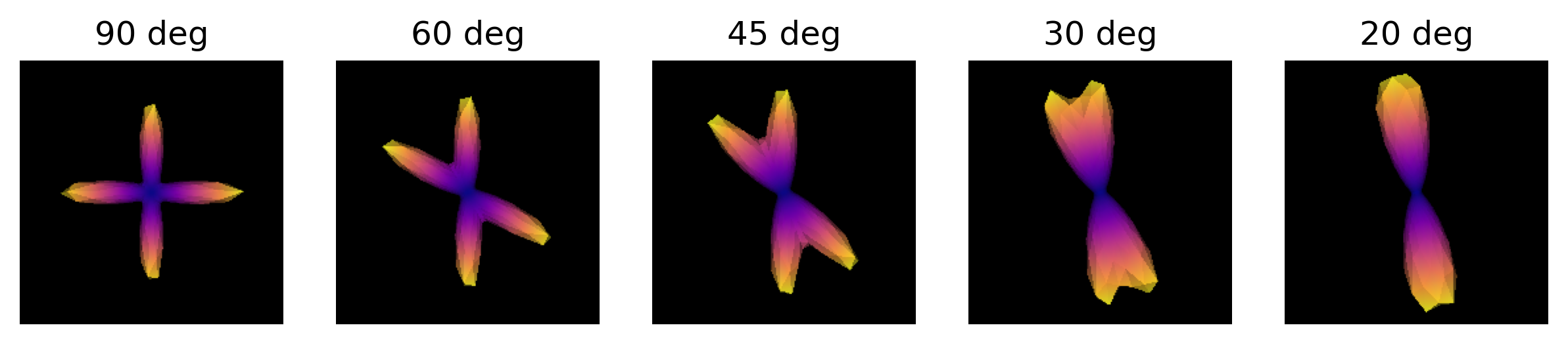
ODFs of different crossing angles.
Tractography
Local tractography
Figure 1
Streamline propagation is, in essence, a numerical analysis
integration problem. The problem lies in finding a curve that joins a
set of discrete local directions. As such, it takes the form of a
differential equation problem of the form: 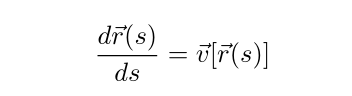
Streamline propagation differential equation
Deterministic tractography
Figure 1
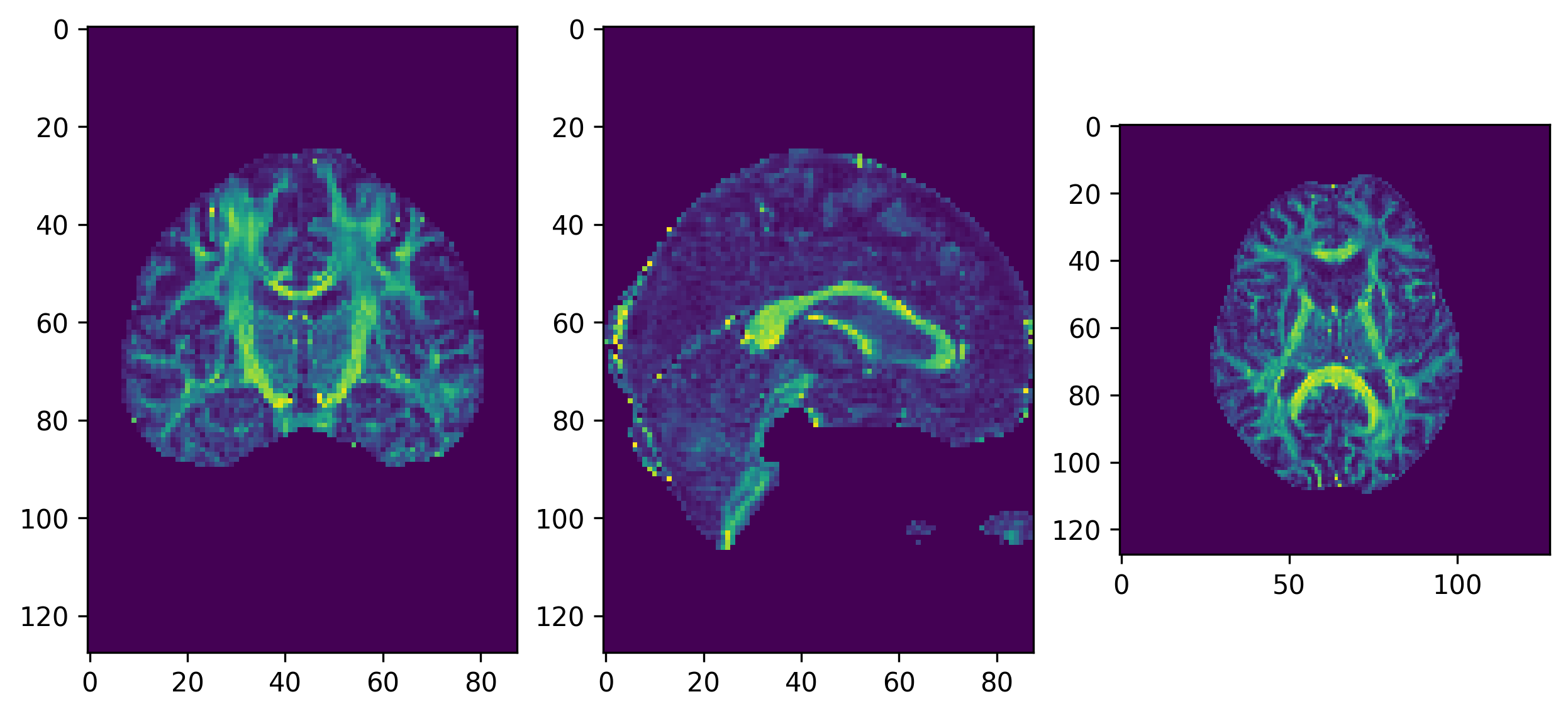
Figure 2
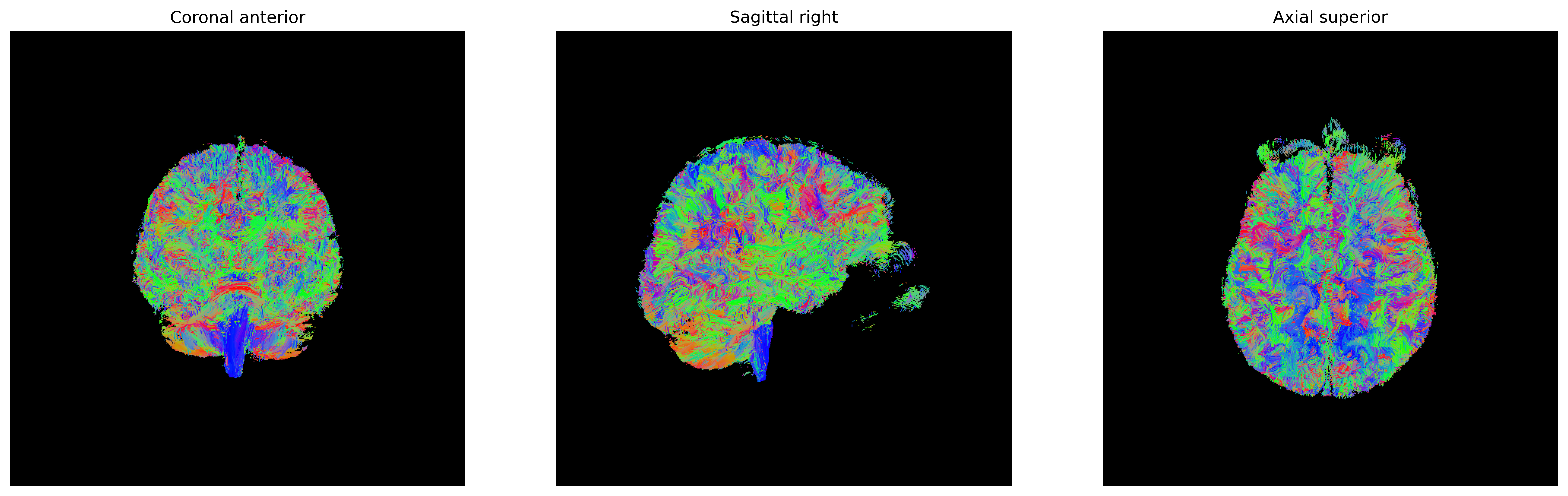
Figure 3
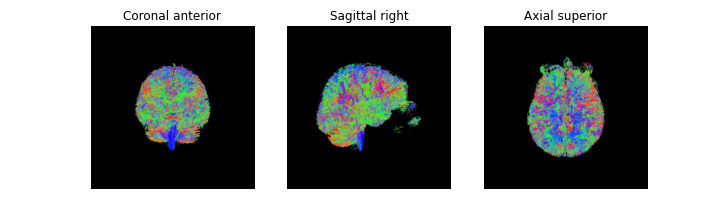
Figure 4
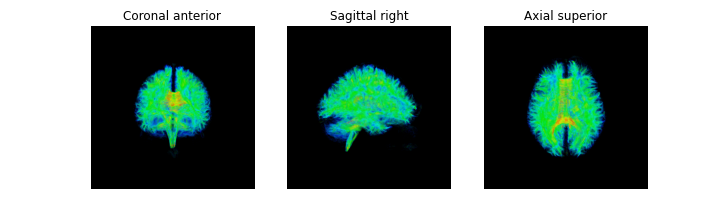
Probabilistic tractography
Figure 1
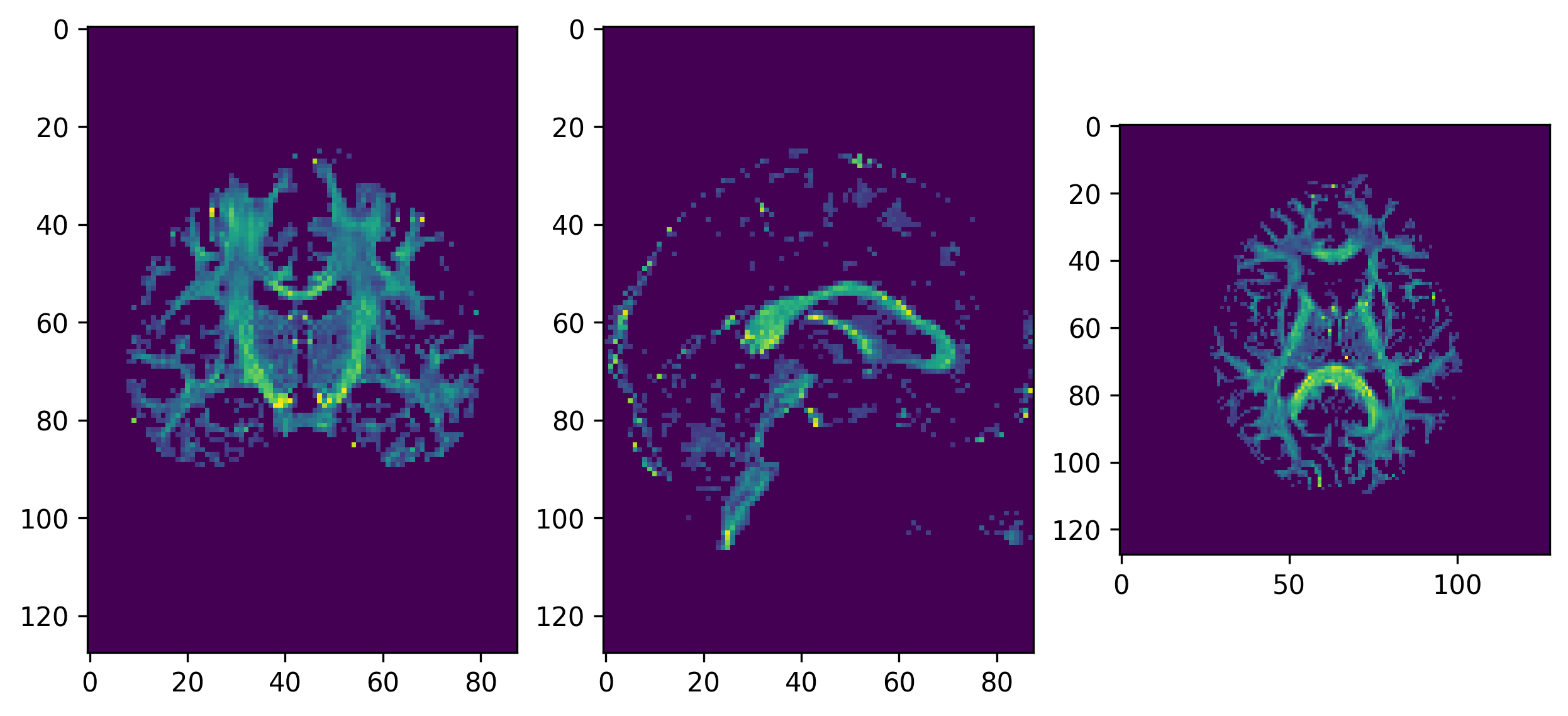
GFA
Figure 2
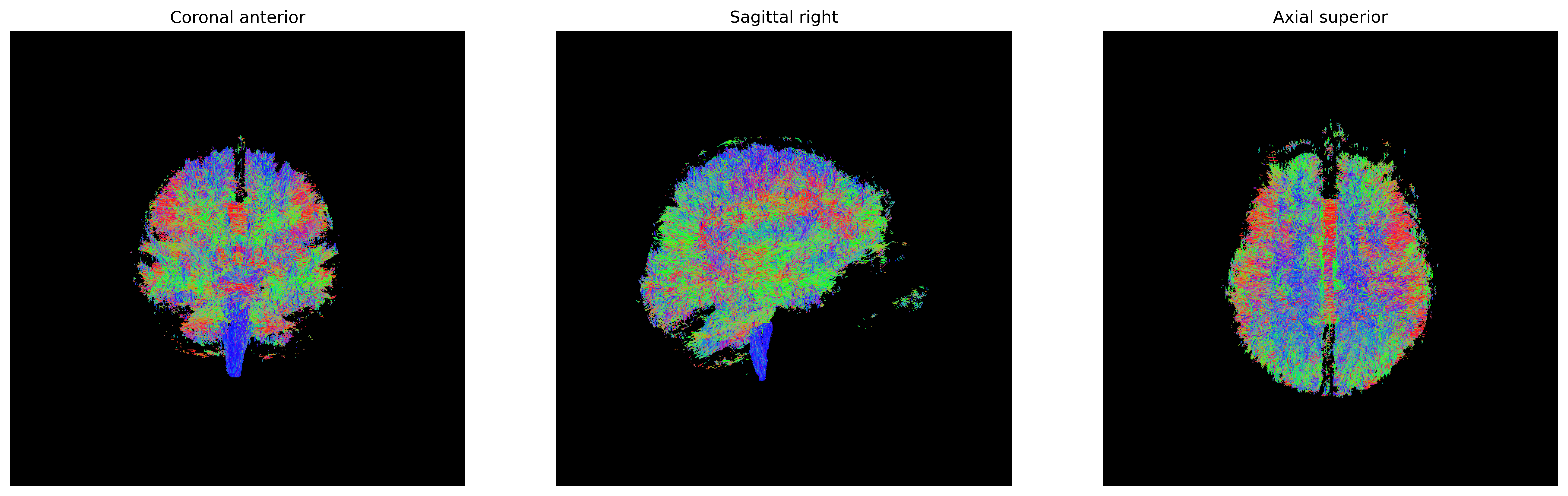
Streamlines representing white matter using probabilistic direction
getter from PMF
Figure 3
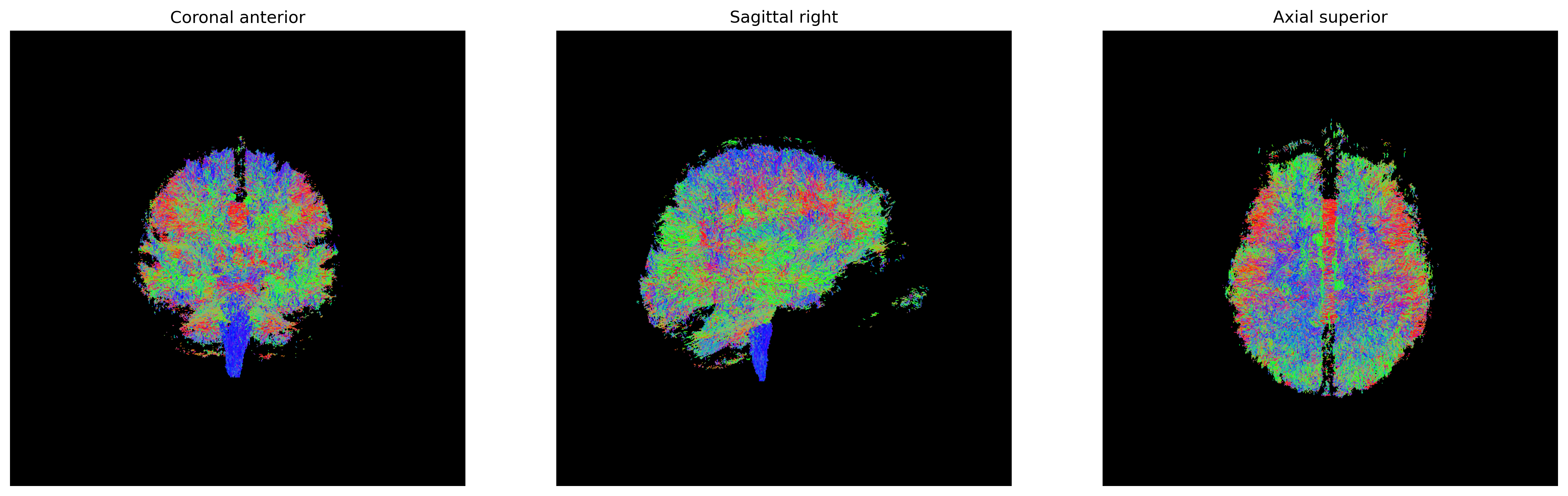
Streamlines representing white matter using probabilistic direction
getter from SH
Figure 4

Peaks obtained from the CSD model for tracking purposes
Figure 5
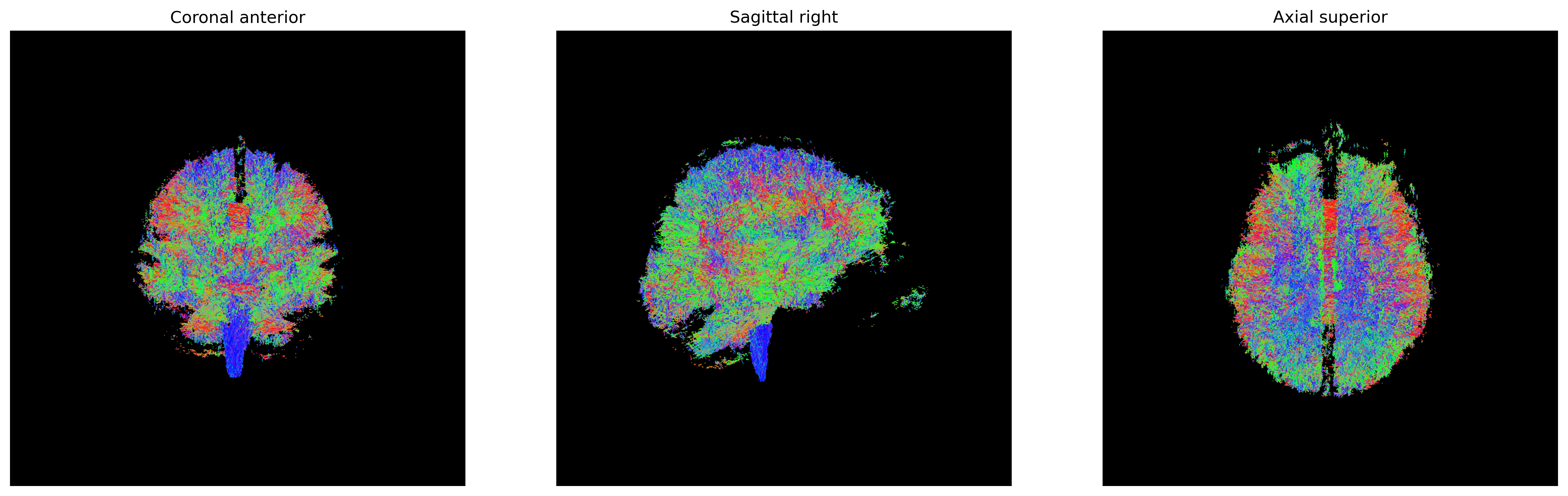
Streamlines representing white matter using probabilistic direction
getter from SH (peaks_from_model)
