Using your GPU with CuPy
Last updated on 2026-03-03 | Edit this page
Estimated time: 270 minutes
Overview
Questions
- “How can I increase the performance of code that uses NumPy?”
- “How can I copy NumPy arrays to the GPU?”
Objectives
- “Be able to indicate if an array, represented by a variable in an iPython shell, is stored in host or device memory.”
- “Be able to copy the contents of this array from host to device memory and vice versa.”
- “Be able to select the appropriate function to either convolve an image using either CPU or GPU compute power.”
- “Be able to quickly estimate the speed benefits for a simple calculation by moving it from the CPU to the GPU.”
Introduction to CuPy
CuPy is a GPU array library that implements a subset of the NumPy and SciPy interfaces. Thanks to CuPy, people conversant with NumPy can very conveniently harvest the compute power of GPUs without writing code in GPU programming languages such as CUDA, OpenCL, and HIP.
From now on we can also use the word host to refer to the CPU on the laptop, desktop, or cluster node you are using as usual, and device to refer to the graphics card and its GPU.
Convolutions in Python
We start by generating an image using Python and NumPy code. We want to compute a convolution on this input image once on the host and once on the device, and then compare both the execution times and the results.
We can write and execute the following code on the host in an iPython
shell or a Jupyter notebook. The pixel values will be zero everywhere
except for a regular grid of single pixels having value one, very much
like a Dirac delta function; hence the input image is named
diracs.
PYTHON
import numpy as np
# Construct an image with repeated delta functions
diracs = np.zeros((2048, 2048))
diracs[8::16,8::16] = 1We can display the top-left corner of the input image to get a feel for how it looks like, as follows:
PYTHON
import pylab as pyl
# Jupyter 'magic' command to render a Matplotlib image in the notebook
%matplotlib inline
# Display the image
# You can zoom in/out using the menu in the window that will appear
pyl.imshow(diracs[0:32, 0:32])
pyl.show()and you should obtain the following image:

Gaussian convolutions
The illustration below shows an example of convolution (courtesy of Michael Plotke, CC BY-SA 3.0, via Wikimedia Commons). Looking at the terminology in the illustration, be forewarned that, inconveniently, the meaning of the word kernel is different when talking of mathematical convolutions and of codes for programming a GPU device. To know more about convolutions, we encourage you to check out this GitHub repository by Vincent Dumoulin and Francesco Visin, who show great animations.
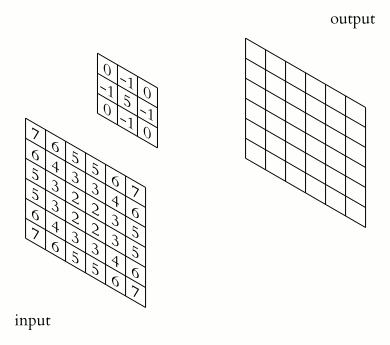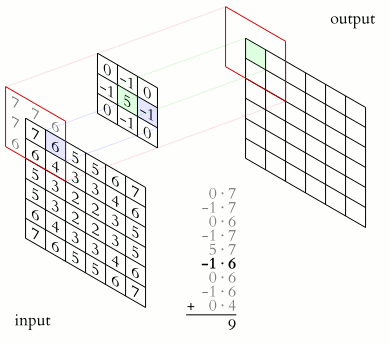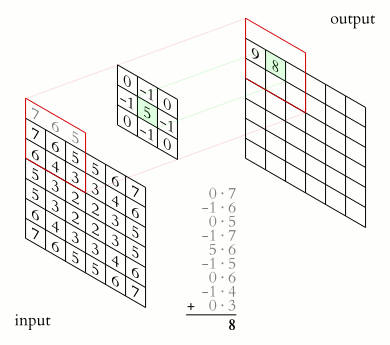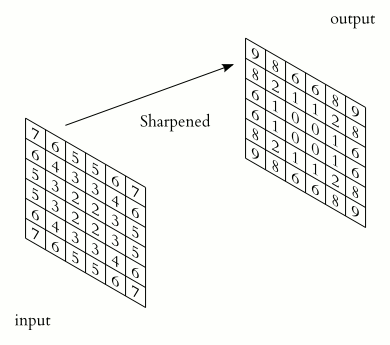
In this course section, we will convolve our image with a 2D Gaussian function, having the general form:
\[G(x,y) = \frac{1}{2\pi \sigma^2} \exp\left(-\frac{x^2 + y^2}{2 \sigma^2}\right)\]
where \(x\) and \(y\) are distances from the origin, and \(\sigma\) controls the width of the curve. Since we can think of an image as a matrix of color values, the convolution of that image with a kernel generates a new matrix with different color values. In particular, convolving images with a 2D Gaussian kernel changes the value of each pixel into a weighted average of the neighboring pixels, thereby smoothing out the features in the input image.
Convolutions are frequently used in computer vision to filter images. For example, Gaussian convolution can be required before applying algorithms for edge detection, which are sensitive to the noise in the original image. To avoid conflicting vocabularies, in the remainder we refer to convolution kernels as filters.
Identifying the dataflow inherent in an algorithm is often useful. Say, if we want to square the numbers in a list, the operations on each item of the list are independent one of another. The dataflow of a one-to-one operation is called a map.
A convolution is slightly more complex because of a many-to-one dataflow, also known as a stencil.
GPUs are exceptionally well suited to compute algorithms that follow either dataflow.
Convolution on the CPU Using SciPy
Let’s first construct and then display the Gaussian filter. Remember that we are still coding everything in standard Python, without using the GPU.
PYTHON
x, y = np.meshgrid(np.linspace(-2, 2, 15), np.linspace(-2, 2, 15))
dist = np.sqrt(x*x + y*y)
sigma = 1
origin = 0.000
gauss = np.exp(-(dist - origin)**2 / (2.0 * sigma**2))
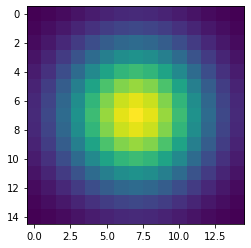
pyl.imshow(gauss)
pyl.show()The code above produces this image of a symmetrical two-dimensional Gaussian surface:
Now we are ready to compute the convolution on the host. Very conveniently, SciPy provides a method for convolutions. Let’s also record the time to perform this convolution and inspect the top-left corner of the convolved image, as follows:
PYTHON
from scipy.signal import convolve2d as convolve2d_cpu
convolved_image_cpu = convolve2d_cpu(diracs, gauss)
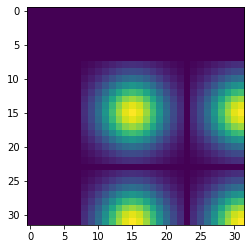
pyl.imshow(convolved_image_cpu[0:32, 0:32])
pyl.show()
%timeit -n 1 -r 1 convolve2d_cpu(diracs, gauss)Obviously, the compute power of your CPU influences the actual execution time very much. We expect that to be in the region of a couple of seconds, as shown in the timing report below:
OUTPUT
2.4 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)Displaying just a corner of the image shows that the Gaussian filter has so much blurred the original pattern of ones surrounded by zeros that we end up with a regular pattern of Gaussians.
Convolution on the GPU Using CuPy
This is a lesson on GPU programming, so let’s use the GPU. In spite of being physically connected – typically with special interconnects – the CPU and the GPU do not share the same memory space. This picture depicts the different components of CPU and GPU and how they are connected:
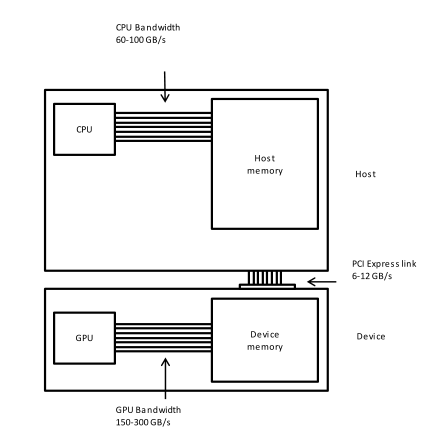
This means that the array created with NumPy is physically stored in
a memory of the host’s and, therefore, is only available to the CPU.
Since our input image and convolution filter are not present in the
device memory yet, we need to copy them to the GPU before executing any
code on it. In practice, we use CuPy to copy the arrays
diracs and gauss from the host’s Random Access
Memory (RAM) to the GPU memory as follows:
Now it is time to compute the convolution on our GPU. Inconveniently,
SciPy does not offer methods running on GPUs. Hence, we import the
convolution function from a CuPy package aliased as cupyx.
Its sub-package cupyx.scipy
performs a selection of the SciPy operations. We will soon verify that
the convolution function of cupyx works out the same
calculations on the GPU as the convolution function of SciPy on the CPU.
In general, CuPy proper and NumPy are so similar one to another as are
the cupyx methods and SciPy; this is intended to invite
programmers already familiar with NumPy and SciPy to use the GPU for
computing. For now, let’s again record the execution time on the device
for the same convolution as the host, and compare the respective
performances.
PYTHON
from cupyx.scipy.signal import convolve2d as convolve2d_gpu
convolved_image_gpu = convolve2d_gpu(diracs_gpu, gauss_gpu)
%timeit -n 7 -r 1 convolved_image_gpu = convolve2d_gpu(diracs_gpu, gauss_gpu)The execution time of the GPU convolution will depend very much on the hardware used, just as seen for the host. The timing using a NVIDIA Tesla T4 at Google Colab was:
OUTPUT
98.2 µs ± 0 ns per loop (mean ± std. dev. of 1 run, 7 loops each)This is way faster than the host: more than a 24000-fold performance improvement, or speedup. Impressive, but is that true?
Measuring performance
So far we used timeit to measure the performance of our
Python code, regardless of whether it was running on the CPU or was
GPU-accelerated. However, the execution on the GPU is
asynchronous: the Python interpreter immediately takes back
control of the program execution, while the GPU is still executing the
task. Therefore, the timing of timeit is not reliable.
Conveniently, cupyx provides the function
benchmark() that measures the actual execution time in the
GPU. The following code executes convolve2d_gpu() with the
appropriate arguments ten times, and stores inside the
.gpu_times attribute of the variable
benchmark_gpu the execution time of each run in
seconds.
PYTHON
from cupyx.profiler import benchmark
benchmark_gpu = benchmark(convolve2d_gpu, (diracs_gpu, gauss_gpu), n_repeat=10)These measurements are also more stable and representative, because
benchmark() disregards the compile time and because the
repetitions warm up the GPU. We can then average the execution times, as
follows:
whereby the performance revisited is:
OUTPUT
0.020642 sWe now have a more reasonable, but still impressive, 116-fold speedup with respect to the execution on the host.
Challenge: convolution on the GPU without CuPy
Try to convolve the NumPy array diracs with the NumPy
array gauss directly on the GPU, that is, without CuPy
arrays. If this works, it will save us the time and effort of
transferring the arrays diracs and gauss to
the GPU.
We can call the GPU convolution function
convolve2d_gpu() directly with diracs and
gauss as argument:
However, this throws a long error message ending with:
OUTPUT
TypeError: Unsupported type <class 'numpy.ndarray'>Unfortunately, it is impossible to access directly from the GPU the NumPy arrays that live in the host RAM.
Validation
To check that the host and the device actually produced the same
output, we compare the two output arrays
convolved_image_gpu and convolved_image_cpu as
follows:
As you may have expected, the outcome of the comparison confirms that the results on the host and on the device are the same:
OUTPUT
array(True)Challenge: fairer comparison of CPU vs. GPU
Compute again the speedup achieved using the GPU, taking into account also the time spent transferring the data from the CPU to the GPU and back.
Hint: use the cp.asnumpy() method to copy a CuPy array
back to the host.
An effective strategy is to time the execution of a single Python function that groups the transfers to and from the GPU and the convolution, as follows:
PYTHON
def push_compute_pull():
diracs_gpu = cp.asarray(diracs)
gauss_gpu = cp.asarray(gauss)
convolved_image_gpu = convolve2d_gpu(diracs_gpu, gauss_gpu)
convolved_image_gpu_in_host = cp.asnumpy(convolved_image_gpu)
benchmark_gpu = benchmark(push_compute_pull, (), n_repeat=10)
gpu_execution_avg = np.average(benchmark_gpu.gpu_times)
print(f"{gpu_execution_avg:.6f} s")OUTPUT
0.035400 sThe speedup taking into account the data transfer decreased from 116
to 67. Nonetheless, accounting for the necessary data transfers is a
better and fairer way to compute performance speedups. As an aside, here
timeit would still provide correct measurements, because
the data transfers force the device and host to sync one with
another.
A shortcut: performing NumPy routines on the GPU
We saw in a previous challenge that we cannot launch the routines of
cupyx directly on NumPy arrays. In fact, we first needed to
transfer the data from the host to the device memory. Conversely, we
also encounter an error when we launch a regular SciPy routine, designed
to run on CPUs, on a CuPy array. Try out the following:
which results in
OUTPUT
...
...
...
TypeError: Implicit conversion to a NumPy array is not allowed.
Please use `.get()` to construct a NumPy array explicitly.So, SciPy routines do not accept CuPy arrays as input. However,
instead of performing a 2D convolution, we can execute a simpler 1D
(linear) convolution that uses the NumPy routine
np.convolve() instead of a SciPy routine. To generate the
input appropriate to a linear convolution, we flatten our input image
from 2D to 1D using the method .ravel(). To generate a 1D
filter, we take the diagonal elements of our 2D Gaussian filter. Let’s
launch a linear convolution on the CPU with the following three
instructions:
PYTHON
diracs_1d_cpu = diracs.ravel()
gauss_1d_cpu = gauss.diagonal()
%timeit -n 1 -r 1 np.convolve(diracs_1d_cpu, gauss_1d_cpu)A realistic execution time is:
OUTPUT
270 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)After having performed this regular linear convolution on the host with NumPy, let’s try something bold. We transfer the 1D arrays to the device and do the convolution with the same NumPy routine, as follows:
PYTHON
diracs_1d_gpu = cp.asarray(diracs_1d_cpu)
gauss_1d_gpu = cp.asarray(gauss_1d_cpu)
benchmark_gpu = benchmark(np.convolve, (diracs_1d_gpu, gauss_1d_gpu), n_repeat=10)
gpu_execution_avg = np.average(benchmark_gpu.gpu_times)
print(f"{gpu_execution_avg:.6f} s")You may be surprised that these commands do not throw any error.
Contrary to SciPy, NumPy routines accept CuPy arrays as input, even
though the latter exist only in GPU memory. Indeed, can you recall that
we validated our codes using a NumPy and a CuPy array as input of
np.allclose()? That worked for the same reason. The
CuPy documentation explains why NumPy routines can handle CuPy
arrays.
The last linear convolution has actually been performed on the GPU, and faster than the CPU:
OUTPUT
0.014529 sWith this Numpy shortcut and without much coding effort, we obtained a good 18-fold speedup.
A scientific application: image processing for radio astronomy
In this section, we will perform four classical steps in image processing for radio astronomy: determination of the background characteristics, segmentation, connected component labeling, and source measurements.
Import the FITS file
We import a 2048²-pixel image of the electromagnetic radiation at 150 MHz around the Galactic Center, as observed by the Indian Giant Metrewave Radio Telescope (GMRT).
The image is stored in this lesson’s
repository as a FITS file. The
astropy Python package enables us to read in this file and,
for compatibility with Python, convert the byte ordering from
the big to little endian, as follows:
Inspect the image
Let’s have a look at this image. Left and right in the data will be
swapped with the method np.fliplr() just to adhere to the
astronomical convention of the right ascension
increasing leftwards.
PYTHON
from matplotlib.colors import LogNorm
maxim = data.max()
fig = pyl.figure(figsize=(50, 12.5))
ax = fig.add_subplot(1, 1, 1)
im_plot = ax.imshow(np.fliplr(data), cmap=pyl.cm.gray_r, norm=LogNorm(vmin = maxim/10, vmax=maxim/100))
pyl.colorbar(im_plot, ax=ax)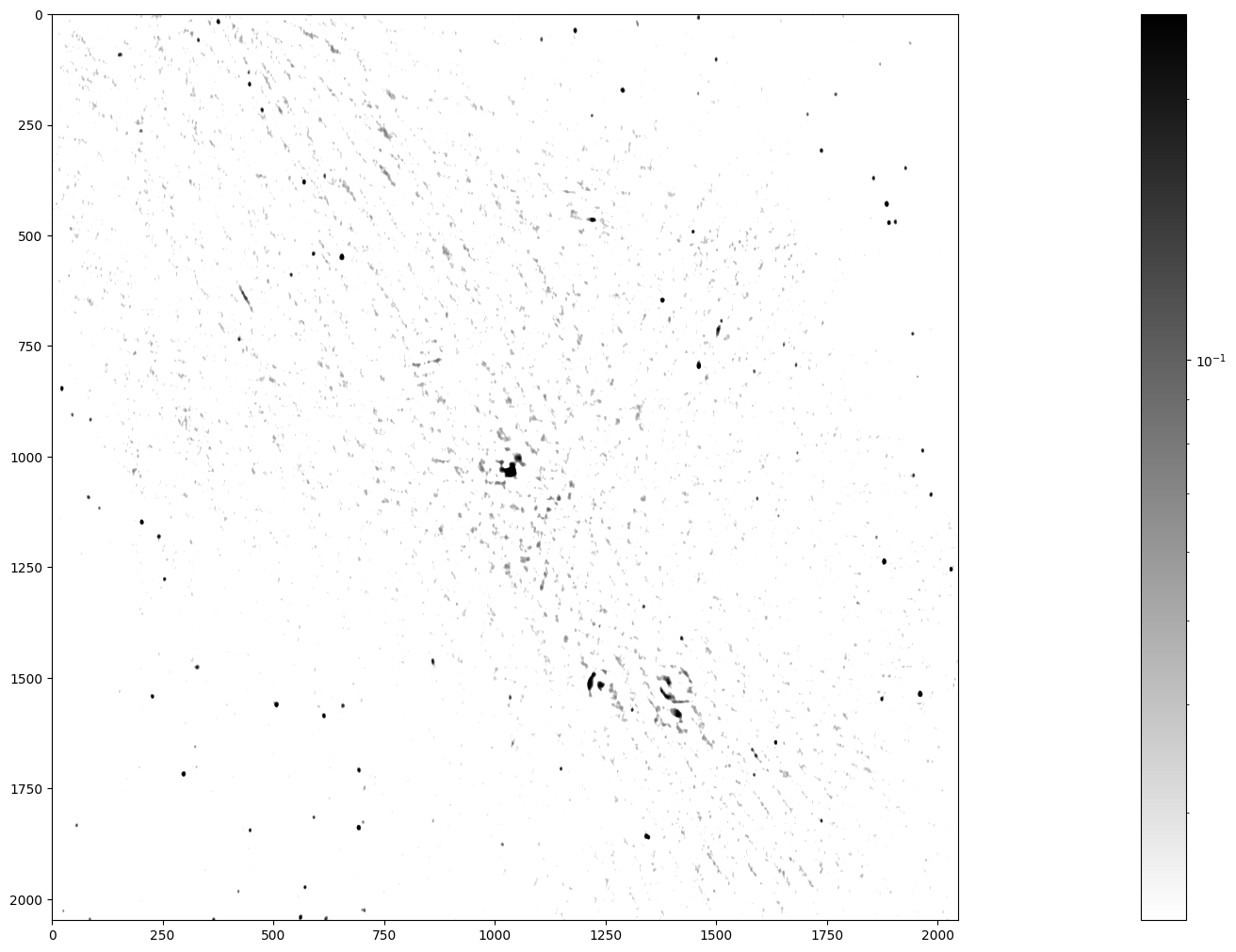
Stars, remnants of supernovas (massive exploded stars), and distant galaxies are possible radiation sources observed in this image. We can spot a few dozen radiation sources in fairly good quality in the lower left and upper right. In contrast, the quality is worse in the diagonal from the upper left to the lower right, because the radio telescope has a limited sensitivity and cannot look into large radiation sources. Nonetheless, you can notice the Galactic Center in the middle of the image and supernova shells as ring-like formations elsewhere.
The telescope accuracy has added background noise to the image. Yet, we want to identify all the radiation sources in this image, determine their positions, and measure their radiation fluxes. How can we then assert whether a high-intensity pixel is a peak of the noise or a genuine source? Assuming that the background noise is normally distributed with standard deviation \(\sigma\), the chance of its intensity being larger than 5\(\sigma\) is 2.9e-7. The chance of picking from our image of 2048² (4.2e6) pixels at least one that is so extremely bright because of noise is thus less than 50%.
Before moving on, let’s determine some summary statistics of the radiation intensity in the input image:
PYTHON
mean_ = data.mean()
median_ = np.median(data)
stddev_ = np.std(data)
max_ = np.amax(data)
print(f"mean = {mean_:.3e}, median = {median_:.3e}, sttdev = {stddev_:.3e}, maximum = {max_:.3e}")This gives (in Jy/beam):
OUTPUT
mean = 3.898e-04, median = 1.571e-05, sttdev = 1.993e-02, maximum = 2.506e+00The maximum flux density is 2506 mJy/beam coming from the Galactic Center, the overall standard deviation 19.9 mJy/beam, and the median 1.57e-05 mJy/beam.
Step 1: Determining the characteristics of the background
First, we separate the background pixels from the source pixels using an iterative procedure called \(\kappa\)-\(\sigma\) clipping, which assumes that high intensity is more likely to result from genuine sources. We start from the standard deviation (\(\sigma\)) and the median (\(\mu_{1/2}\)) of all pixel intensities, as computed above. We then discard (clip) the pixels whose intensity is larger than \(\mu_{1/2} + 3\sigma\) or smaller than \(\mu_{1/2} - 3\sigma\). In the next pass, we compute again the median and standard deviation of the clipped set, and clip once more. We repeat these operations until no more pixels are clipped, that is, there are no outliers in the designated tails.
In the meantime, you may have noticed already that \(\kappa\)-\(\sigma\) clipping is a compute intensive task that could be implemented in a GPU. For the moment, let’s implement the algorithm with the NumPy code for a CPU, as follows:
PYTHON
# Flattening our 2D data makes subsequent steps easier
data_flat = data.ravel()
# Here is a kappa-sigma clipper for the CPU
def ks_clipper_cpu(data_flat):
while True:
med = np.median(data_flat)
std = np.std(data_flat)
clipped_below = data_flat.compress(data_flat > med - 3 * std)
clipped_data = clipped_below.compress(clipped_below < med + 3 * std)
if len(clipped_data) == len(data_flat):
break
data_flat = clipped_data
return data_flat
data_clipped_cpu = ks_clipper_cpu(data_flat)
timing_ks_clipping_cpu = %timeit -o ks_clipper_cpu(data_flat)
fastest_ks_clipping_cpu = timing_ks_clipping_cpu.best
print(f"Fastest ks clipping time on CPU = {1000 * fastest_ks_clipping_cpu:.3e} ms.")The performance is close to 1 s and, hopefully, can be sped up on the GPU.
OUTPUT
793 ms ± 17.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Fastest ks clipping time on CPU = 7.777e+02 ms.Finally, let’s see how the \(\kappa\)-\(\sigma\) clipping has influenced the summary statistics:
PYTHON
clipped_mean_ = data_clipped.mean()
clipped_median_ = np.median(data_clipped_cpu)
clipped_stddev_ = np.std(data_clipped_cpu)
clipped_max_ = np.amax(data_clipped_cpu)
print(f"mean of clipped = {clipped_mean_:.3e},
median of clipped = {clipped_median_:.3e} \n
standard deviation of clipped = {clipped_stddev_:.3e},
maximum of clipped = {clipped_max_:.3e}")The first-order statistics have become smaller, which reassures us
that data_clipped contains background pixels:
OUTPUT
mean of clipped = -1.945e-06, median of clipped = -9.796e-06
standard deviation of clipped = 1.334e-02, maximum of clipped = 4.000e-02The standard deviation of the intensity in the background pixels is be the basis for the next step.
Challenge: \(\kappa\)-\(\sigma\) clipping on the GPU
Now that you know how the \(\kappa\)-\(\sigma\) clipping algorithm works, perform it on the GPU using CuPy. Compute the speedup, including the data transfer to and from the GPU.
PYTHON
def ks_clipper_gpu(data_flat):
data_flat_gpu = cp.asarray(data_flat)
data_gpu_clipped = ks_clipper_cpu(data_flat_gpu)
return cp.asnumpy(data_gpu_clipped)
data_clipped_gpu = ks_clipper_gpu(data_flat)
timing_ks_clipping_gpu = benchmark(ks_clipper_gpu,
(data_flat, ),
n_repeat=10)
fastest_ks_clipping_gpu = np.amin(timing_ks_clipping_gpu.gpu_times)
print(f"{1000 * fastest_ks_clipping_gpu:.3e} ms")OUTPUT
6.329e+01 msPYTHON
speedup_factor = fastest_ks_clipping_cpu/fastest_ks_clipping_gpu
print(f"The speedup factor for ks clipping is: {speedup_factor:.3e}")OUTPUT
The speedup factor for ks clipping is: 1.232e+01Step 2: Segmenting the image
We have already estimated that clipping an image of 2048² pixels at the \(5 \sigma\) level yields a chance of less than 50% that at least one out of all the sources we detect is a noise peak. So let’s set the threshold at \(5\sigma\) and segment it.
First let’s check that the standard deviation from our clipper on the GPU is the same:
PYTHON
stddev_gpu_ = np.std(data_clipped_gpu)
print(f"standard deviation of background_noise = {stddev_gpu_:.4f} Jy/beam")OUTPUT
standard deviation of background_noise = 0.0133 Jy/beamWe then apply the \(5 \sigma\) threshold to the image with this standard deviation:
PYTHON
threshold = 5 * stddev_gpu_
segmented_image = np.where(data > threshold, 1, 0)
timing_segmentation_CPU = %timeit -o np.where(data > threshold, 1, 0)
fastest_segmentation_CPU = timing_segmentation_CPU.best
print(f"Fastest CPU segmentation time = {1000 * fastest_segmentation_CPU:.3e} ms.")OUTPUT
6.41 ms ± 55.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Fastest CPU segmentation time = 6.294e+00 ms.Step 3: Labeling the segmented data
This is called connected component labeling (CCL). It will replace pixel values in the segmented image - just consisting of zeros and ones - of the first connected group of pixels with the value 1 - so nothing changed, but just for that first group - the pixel values in the second group of connected pixels will all be 2, the third connected group of pixels will all have the value 3 etc.
This is a CPU code for connected component labeling.
PYTHON
from scipy.ndimage import label as label_cpu
labeled_image = np.empty(data.shape)
number_of_sources_in_image = label_cpu(segmented_image, output = labeled_image)
sigma_unicode = "\u03C3"
print(f"The number of sources in the image at the 5{sigma_unicode} level is {number_of_sources_in_image}.")
timing_CCL_CPU = %timeit -o label_cpu(segmented_image, output = labeled_image)
fastest_CCL_CPU = timing_CCL_CPU.best
print(f"Fastest CPU CCL time = {1000 * fastest_CCL_CPU:.3e} ms.")This gives, on my machine:
OUTPUT
The number of sources in the image at the 5σ level is 185.
26.3 ms ± 965 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Fastest CPU CCL time = 2.546e+01 ms.Let’s not just accept the answer, and let’s do a sanity check. What are the values in the labeled image?
PYTHON
print(f"These are all the pixel values we can find in the labeled image: {np.unique(labeled_image)}")This should show the following output:
OUTPUT
These are all the pixel values we can find in the labeled image:
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27.
28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41.
42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55.
56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69.
70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83.
84. 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97.
98. 99. 100. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111.
112. 113. 114. 115. 116. 117. 118. 119. 120. 121. 122. 123. 124. 125.
126. 127. 128. 129. 130. 131. 132. 133. 134. 135. 136. 137. 138. 139.
140. 141. 142. 143. 144. 145. 146. 147. 148. 149. 150. 151. 152. 153.
154. 155. 156. 157. 158. 159. 160. 161. 162. 163. 164. 165. 166. 167.
168. 169. 170. 171. 172. 173. 174. 175. 176. 177. 178. 179. 180. 181.
182. 183. 184. 185.]Step 4: Measuring the radiation sources
We are ready for the final step. We have been given observing time to make this beautiful image of the Galactic Center, we have determined its background statistics, we have separated actual cosmic sources from noise and now we want to measure these cosmic sources. What are their positions and what are their flux densities?
Again, the algorithms from scipy.ndimage help us to
determine these quantities. This is the CPU code for measuring our
sources.
PYTHON
from scipy.ndimage import center_of_mass as com_cpu
from scipy.ndimage import sum_labels as sl_cpu
all_positions = com_cpu(data, labeled_image,
range(1, number_of_sources_in_image+1))
all_integrated_fluxes = sl_cpu(data, labeled_image,
range(1, number_of_sources_in_image+1))
print (f'These are the ten highest integrated fluxes of the sources in my \n image: {np.sort(all_integrated_fluxes)[-10:]}')which gives the Galactic Center as the most luminous source, which makes sense when we look at our image.
OUTPUT
These are the ten highest integrated fluxes of the sources in my image:
[ 38.90615184 41.91485894 43.02203498 47.30590784 51.23707351
58.07289425 68.85673917 70.31223921 95.16443585 363.58937774]Now we can try to measure the execution times for both algorithms, like this:
PYTHON
%%timeit -o
all_positions = com_cpu(data, labeled_image,
range(1, number_of_sources_in_image+1))
all_integrated_fluxes = sl_cpu(data, labeled_image,
range(1, number_of_sources_in_image+1))which yields, on my machine:
OUTPUT
797 ms ± 9.32 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
<TimeitResult : 797 ms ± 9.32 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)>To collect the result from that timing in our next cell block, we
need a trick that uses the _ variable.
PYTHON
timing_source_measurements_CPU = _
fastest_source_measurements_CPU = timing_source_measurements_CPU.best
print(f"Fastest CPU set of source measurements = {1000 * fastest_source_measurements_CPU:.3e} ms.")which yields
OUTPUT
Fastest CPU set of source measurements = 7.838e+02 ms.Challenge: putting it all together
Combine the first two steps of image processing for astronomy, i.e. determining background characteristics e.g. through \(\kappa\)-\(\sigma\) clipping and segmentation into a single function, that works for both CPU and GPU. Next, write a function for connected component labeling and source measurements on the GPU and calculate the overall speedup factor for the combined four steps of image processing in astronomy on the GPU relative to the CPU. Finally, verify your output by comparing with the previous output, using the CPU.
PYTHON
def first_two_steps_for_both_CPU_and_GPU(data):
data_flat = data.ravel()
data_clipped = ks_clipper_cpu(data_flat)
stddev_ = np.std(data_clipped)
threshold = 5 * stddev_
segmented_image = np.where(data > threshold, 1, 0)
return segmented_image
def ccl_and_source_measurements_on_CPU(data_CPU, segmented_image_CPU):
labeled_image_CPU = np.empty(data_CPU.shape)
number_of_sources_in_image = label_cpu(segmented_image_CPU,
output= labeled_image_CPU)
all_positions = com_cpu(data_CPU, labeled_image_CPU,
np.arange(1, number_of_sources_in_image+1))
all_fluxes = sl_cpu(data_CPU, labeled_image_CPU,
np.arange(1, number_of_sources_in_image+1))
return np.array(all_positions), np.array(all_fluxes)
CPU_output = ccl_and_source_measurements_on_CPU(data,
first_two_steps_for_both_CPU_and_GPU(data))
timing_complete_processing_CPU = benchmark(
ccl_and_source_measurements_on_CPU,
(data,
first_two_steps_for_both_CPU_and_GPU(data)), n_repeat=10)
fastest_complete_processing_CPU = np.amin(timing_complete_processing_CPU.cpu_times)
print(f"The four steps of image processing for astronomy take {1000 * fastest_complete_processing_CPU:.3e} ms\n on our CPU.")
from cupyx.scipy.ndimage import label as label_gpu
from cupyx.scipy.ndimage import center_of_mass as com_gpu
from cupyx.scipy.ndimage import sum_labels as sl_gpu
def ccl_and_source_measurements_on_GPU(data_GPU, segmented_image_GPU):
labeled_image_GPU = cp.empty(data_GPU.shape)
number_of_sources_in_image = label_gpu(segmented_image_GPU,
output= labeled_image_GPU)
all_positions = com_gpu(data_GPU, labeled_image_GPU,
cp.arange(1, number_of_sources_in_image+1))
all_fluxes = sl_gpu(data_GPU, labeled_image_GPU,
cp.arange(1, number_of_sources_in_image+1))
# This seems redundant, but we want to return ndarrays (Numpy)
# and what we have are lists.
# These first have to be converted to
# Cupy arrays before they can be converted to Numpy arrays.
return cp.asnumpy(cp.asarray(all_positions)),
cp.asnumpy(cp.asarray(all_fluxes))
GPU_output = ccl_and_source_measurements_on_GPU(cp.asarray(data), first_two_steps_for_both_CPU_and_GPU(cp.asarray(data)))
timing_complete_processing_GPU = benchmark(ccl_and_source_measurements_on_GPU, (cp.asarray(data), first_two_steps_for_both_CPU_and_GPU(cp.asarray(data))), n_repeat=10)
fastest_complete_processing_GPU = np.amin(timing_complete_processing_GPU.gpu_times)
print(f"The four steps of image processing for astronomy take {1000 * fastest_complete_processing_GPU:.3e} ms\n on our GPU.")
overall_speedup_factor = fastest_complete_processing_CPU / fastest_complete_processing_GPU
print(f"This means that the overall speedup factor GPU vs CPU equals: {overall_speedup_factor:.3e}\n")
all_positions_agree = np.allclose(CPU_output[0], GPU_output[0])
print(f"The CPU and GPU positions agree: {all_positions_agree}\n")
all_fluxes_agree = np.allclose(CPU_output[1], GPU_output[1])
print(f"The CPU and GPU fluxes agree: {all_positions_agree}\n")OUTPUT
The four steps of image processing for astronomy take 1.060e+03 ms on our CPU.
The four steps of image processing for astronomy take 5.770e+01 ms on our GPU.
This means that the overall speedup factor GPU vs _mCPU equals: 1.838e+01
The CPU and GPU positions agree: True
The CPU and GPU fluxes agree: True- “CuPy provides GPU accelerated version of many NumPy and Scipy functions.”
- “Always have CPU and GPU versions of your code so that you can compare performance, as well as validate your code.”
