Working with large data

Estimated time: 12 minutes

Overview

Questions

• How do we work with single-cell datasets that are too large to fit in memory?
• How do we speed up single-cell analysis workflows for large datasets?
• How do we convert between popular single-cell data formats?

Objectives

• Work with out-of-memory data representations such as HDF5.
• Speed up single-cell analysis with parallel computation.
• Invoke fast approximations for essential analysis steps.
• Convert SingleCellExperiment objects to SeuratObjects and AnnData objects.

Motivation

---

Advances in scRNA-seq technologies have increased the number of cells that can be assayed in routine experiments. Public databases such as GEO are continually expanding with more scRNA-seq studies, while large-scale projects such as the Human Cell Atlas are expected to generate data for billions of cells. For effective data analysis, the computational methods need to scale with the increasing size of scRNA-seq data sets. This section discusses how we can use various aspects of the Bioconductor ecosystem to tune our analysis pipelines for greater speed and efficiency.

Out of memory representations

---

The count matrix is the central structure around which our analyses are based. In most of the previous chapters, this has been held fully in memory as a dense matrix or as a sparse dgCMatrix. Howevever, in-memory representations may not be feasible for very large data sets, especially on machines with limited memory. For example, the 1.3 million brain cell data set from 10X Genomics (Zheng et al., 2017) would require over 100 GB of RAM to hold as a matrix and around 30 GB as a dgCMatrix. This makes it challenging to explore the data on anything less than a HPC system.

The obvious solution is to use a file-backed matrix representation where the data are held on disk and subsets are retrieved into memory as requested. While a number of implementations of file-backed matrices are available (e.g., bigmemory, matter), we will be using the implementation from the HDF5Array package. This uses the popular HDF5 format as the underlying data store, which provides a measure of standardization and portability across systems. We demonstrate with a subset of 20,000 cells from the 1.3 million brain cell data set, as provided by the TENxBrainData package.

R

library(TENxBrainData)

sce.brain <- TENxBrainData20k() 

sce.brain

OUTPUT

class: SingleCellExperiment
dim: 27998 20000
metadata(0):
assays(1): counts
rownames: NULL
rowData names(2): Ensembl Symbol
colnames: NULL
colData names(4): Barcode Sequence Library Mouse
reducedDimNames(0):
mainExpName: NULL
altExpNames(0):

Examination of the SingleCellExperiment object indicates that the count matrix is a HDF5Matrix. From a comparison of the memory usage, it is clear that this matrix object is simply a stub that points to the much larger HDF5 file that actually contains the data. This avoids the need for large RAM availability during analyses.

R

counts(sce.brain)

OUTPUT

<27998 x 20000> HDF5Matrix object of type "integer":
             [,1]     [,2]     [,3]     [,4] ... [,19997] [,19998] [,19999]
    [1,]        0        0        0        0   .        0        0        0
    [2,]        0        0        0        0   .        0        0        0
    [3,]        0        0        0        0   .        0        0        0
    [4,]        0        0        0        0   .        0        0        0
    [5,]        0        0        0        0   .        0        0        0
     ...        .        .        .        .   .        .        .        .
[27994,]        0        0        0        0   .        0        0        0
[27995,]        0        0        0        1   .        0        2        0
[27996,]        0        0        0        0   .        0        1        0
[27997,]        0        0        0        0   .        0        0        0
[27998,]        0        0        0        0   .        0        0        0
         [,20000]
    [1,]        0
    [2,]        0
    [3,]        0
    [4,]        0
    [5,]        0
     ...        .
[27994,]        0
[27995,]        0
[27996,]        0
[27997,]        0
[27998,]        0

R

object.size(counts(sce.brain))

OUTPUT

2496 bytes

R

file.info(path(counts(sce.brain)))$size

OUTPUT

[1] 76264332

Manipulation of the count matrix will generally result in the creation of a DelayedArray object from the DelayedArray package. This remembers the operations to be applied to the counts and stores them in the object, to be executed when the modified matrix values are realized for use in calculations. The use of delayed operations avoids the need to write the modified values to a new file at every operation, which would unnecessarily require time-consuming disk I/O.

R

tmp <- counts(sce.brain)

tmp <- log2(tmp + 1)

tmp

OUTPUT

<27998 x 20000> DelayedMatrix object of type "double":
             [,1]     [,2]     [,3] ... [,19999] [,20000]
    [1,]        0        0        0   .        0        0
    [2,]        0        0        0   .        0        0
    [3,]        0        0        0   .        0        0
    [4,]        0        0        0   .        0        0
    [5,]        0        0        0   .        0        0
     ...        .        .        .   .        .        .
[27994,]        0        0        0   .        0        0
[27995,]        0        0        0   .        0        0
[27996,]        0        0        0   .        0        0
[27997,]        0        0        0   .        0        0
[27998,]        0        0        0   .        0        0

Many functions described in the previous workflows are capable of accepting HDF5Matrix objects. This is powered by the availability of common methods for all matrix representations (e.g., subsetting, combining, methods from DelayedMatrixStats as well as representation-agnostic C++ code using beachmat. For example, we compute QC metrics below with the same calculateQCMetrics() function that we used in the other workflows.

R

library(scater)

is.mito <- grepl("^mt-", rowData(sce.brain)$Symbol)

qcstats <- perCellQCMetrics(sce.brain, subsets = list(Mt = is.mito))

qcstats

OUTPUT

DataFrame with 20000 rows and 6 columns
            sum  detected subsets_Mt_sum subsets_Mt_detected subsets_Mt_percent
      <numeric> <numeric>      <numeric>           <numeric>          <numeric>
1          3060      1546            123                  10            4.01961
2          3500      1694            118                  11            3.37143
3          3092      1613             58                   9            1.87581
4          4420      2050            131                  10            2.96380
5          3771      1813            100                   8            2.65182
...         ...       ...            ...                 ...                ...
19996      4431      2050            127                   9           2.866170
19997      6988      2704             60                   9           0.858615
19998      8749      2988            305                  11           3.486113
19999      3842      1711            129                   8           3.357626
20000      1775       945             26                   6           1.464789
          total
      <numeric>
1          3060
2          3500
3          3092
4          4420
5          3771
...         ...
19996      4431
19997      6988
19998      8749
19999      3842
20000      1775

Needless to say, data access from file-backed representations is slower than that from in-memory representations. The time spent retrieving data from disk is an unavoidable cost of reducing memory usage. Whether this is tolerable depends on the application. One example usage pattern involves performing the heavy computing quickly with in-memory representations on HPC systems with plentiful memory, and then distributing file-backed counterparts to individual users for exploration and visualization on their personal machines.

Parallelization

---

Parallelization of calculations across genes or cells is an obvious strategy for speeding up scRNA-seq analysis workflows.

The BiocParallel package provides a common interface for parallel computing throughout the Bioconductor ecosystem, manifesting as a BPPARAM argument in compatible functions. We can also use BiocParallel with more expressive functions directly through the package’s interface.

Basic use

R

library(BiocParallel)

BiocParallel makes it quite easy to iterate over a vector and distribute the computation across workers using the bplapply function. Basic knowledge of lapply is required.

In this example, we find the square root of a vector of numbers in parallel by indicating the BPPARAM argument in bplapply.

R

param <- MulticoreParam(workers = 1)

bplapply(
    X = c(4, 9, 16, 25),
    FUN = sqrt,
    BPPARAM = param
)

OUTPUT

[[1]]
[1] 2

[[2]]
[1] 3

[[3]]
[1] 4

[[4]]
[1] 5

Note. The number of workers is set to 1 due to continuous testing resource limitations.

There exists a diverse set of parallelization backends depending on available hardware and operating systems.

For example, we might use forking across two cores to parallelize the variance calculations on a Unix system:

R

library(MouseGastrulationData)

library(scran)

sce <- WTChimeraData(samples = 5, type = "processed")

sce <- logNormCounts(sce)

dec.mc <- modelGeneVar(sce, BPPARAM = MulticoreParam(2))

dec.mc

OUTPUT

DataFrame with 29453 rows and 6 columns
                          mean       total        tech         bio     p.value
                     <numeric>   <numeric>   <numeric>   <numeric>   <numeric>
ENSMUSG00000051951 0.002800256 0.003504940 0.002856697 6.48243e-04 1.20905e-01
ENSMUSG00000089699 0.000000000 0.000000000 0.000000000 0.00000e+00         NaN
ENSMUSG00000102343 0.000000000 0.000000000 0.000000000 0.00000e+00         NaN
ENSMUSG00000025900 0.000794995 0.000863633 0.000811019 5.26143e-05 3.68953e-01
ENSMUSG00000025902 0.170777718 0.388633677 0.170891603 2.17742e-01 2.47893e-11
...                        ...         ...         ...         ...         ...
ENSMUSG00000095041  0.35571083  0.34572194  0.33640994  0.00931199    0.443233
ENSMUSG00000063897  0.49007956  0.41924282  0.44078158 -0.02153876    0.599499
ENSMUSG00000096730  0.00000000  0.00000000  0.00000000  0.00000000         NaN
ENSMUSG00000095742  0.00177158  0.00211619  0.00180729  0.00030890    0.188992
tomato-td           0.57257331  0.47487832  0.49719425 -0.02231593    0.591542
                           FDR
                     <numeric>
ENSMUSG00000051951 6.76255e-01
ENSMUSG00000089699         NaN
ENSMUSG00000102343         NaN
ENSMUSG00000025900 7.56202e-01
ENSMUSG00000025902 1.35508e-09
...                        ...
ENSMUSG00000095041    0.756202
ENSMUSG00000063897    0.756202
ENSMUSG00000096730         NaN
ENSMUSG00000095742    0.756202
tomato-td             0.756202

Another approach would be to distribute jobs across a network of computers, which yields the same result:

R

dec.snow <- modelGeneVar(sce, BPPARAM = SnowParam(2))

For high-performance computing (HPC) systems with a cluster of compute nodes, we can distribute jobs via the job scheduler using the BatchtoolsParam class. The example below assumes a SLURM cluster, though the settings can be easily configured for a particular system (see here for details).

R

# 2 hours, 8 GB, 1 CPU per task, for 10 tasks.
rs <- list(walltime = 7200, memory = 8000, ncpus = 1)

bpp <- BatchtoolsParam(10, cluster = "slurm", resources = rs)

Parallelization is best suited for independent, CPU-intensive tasks where the division of labor results in a concomitant reduction in compute time. It is not suited for tasks that are bounded by other compute resources, e.g., memory or file I/O (though the latter is less of an issue on HPC systems with parallel read/write). In particular, R itself is inherently single-core, so many of the parallelization backends involve (i) setting up one or more separate R sessions, (ii) loading the relevant packages and (iii) transmitting the data to that session. Depending on the nature and size of the task, this overhead may outweigh any benefit from parallel computing. While the default behavior of the parallel job managers often works well for simple cases, it is sometimes necessary to explicitly specify what data/libraries are sent to / loaded on the parallel workers in order to avoid unnecessary overhead.

Challenge

How do you turn on progress bars with parallel processing?

Show me the solution

From ?MulticoreParam :

progressbar logical(1) Enable progress bar (based on plyr:::progress_text). Enabling the progress bar changes the default value of tasks to .Machine$integer.max, so that progress is reported for each element of X.

Progress bars are a helpful way to gauge whether that task is going to take 5 minutes or 5 hours.

Fast approximations

---

Nearest neighbor searching

Identification of neighbouring cells in PC or expression space is a common procedure that is used in many functions, e.g., buildSNNGraph(), doubletCells(). The default is to favour accuracy over speed by using an exact nearest neighbour (NN) search, implemented with the \(k\)-means for \(k\)-nearest neighbours algorithm. However, for large data sets, it may be preferable to use a faster approximate approach.

The BiocNeighbors framework makes it easy to switch between search options by simply changing the BNPARAM argument in compatible functions. To demonstrate, we will use the wild-type chimera data for which we had applied graph-based clustering using the Louvain algorithm for community detection:

R

library(bluster)

sce <- runPCA(sce)

colLabels(sce) <- clusterCells(sce, use.dimred = "PCA",
                               BLUSPARAM = NNGraphParam(cluster.fun = "louvain"))

The above clusters on a nearest neighbor graph generated with an exact neighbour search. We repeat this below using an approximate search, implemented using the Annoy algorithm. This involves constructing a AnnoyParam object to specify the search algorithm and then passing it to the parameterization of the NNGraphParam() function. The results from the exact and approximate searches are consistent with most clusters from the former re-appearing in the latter. This suggests that the inaccuracy from the approximation can be largely ignored.

R

library(scran)

library(BiocNeighbors)

clusters <- clusterCells(sce, use.dimred = "PCA",
                         BLUSPARAM = NNGraphParam(cluster.fun = "louvain",
                                                  BNPARAM = AnnoyParam()))

table(exact = colLabels(sce), approx = clusters)

OUTPUT

     approx
exact   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15
   1   95   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   2    0 143   0   0   0   0   0   0   0   0   0   0   0   0   1
   3    0   0  77   0   0   0   0   0   0   0   0   0   0   0   0
   4    0   0   0 341   0   0   0   0   0   0   0   0   0   0   0
   5    0   0   0   0 390   0   0   2   0   0   0   0   0   0   0
   6    0   0   0   0   0 210 245   0   0   1   0   2   1   0   0
   7    0   0   0   0   0   0   0  92   0   0   0   0   0   0   0
   8    1   0   0   0   1   0   0   0 106   0   0   0   0   0   0
   9    0   0   0   0   0   0   0   0   0 113   0   0   0   0   0
   10   0   0   0   0   0   0   0   0   0   5 142   0   6   0   0
   11   0   0   0   0   2   0   0   2   0  10   0 202   0   0   0
   12   0   0   0   0   0   0   0   0   0   0   0   0 145   0   0
   13   0   0   0   0   0   0   0   0   0   0   0   0   0  20   0
   14   0   0   0   0   0   0   0   0   0   0   0   0   0   0  56

The similarity of the two clusterings can be quantified by calculating the pairwise Rand index:

R

rand <- pairwiseRand(colLabels(sce), clusters, mode = "index")

stopifnot(rand > 0.8)

Note that Annoy writes the NN index to disk prior to performing the search. Thus, it may not actually be faster than the default exact algorithm for small datasets, depending on whether the overhead of disk write is offset by the computational complexity of the search. It is also not difficult to find situations where the approximation deteriorates, especially at high dimensions, though this may not have an appreciable impact on the biological conclusions.

R

set.seed(1000)

y1 <- matrix(rnorm(50000), nrow = 1000)

y2 <- matrix(rnorm(50000), nrow = 1000)

Y <- rbind(y1, y2)

exact <- findKNN(Y, k = 20)

approx <- findKNN(Y, k = 20, BNPARAM = AnnoyParam())

mean(exact$index != approx$index)

OUTPUT

[1] 0.561925

Singular value decomposition

The singular value decomposition (SVD) underlies the PCA used throughout our analyses, e.g., in denoisePCA(), fastMNN(), doubletCells(). (Briefly, the right singular vectors are the eigenvectors of the gene-gene covariance matrix, where each eigenvector represents the axis of maximum remaining variation in the PCA.) The default base::svd() function performs an exact SVD that is not performant for large datasets. Instead, we use fast approximate methods from the irlba and rsvd packages, conveniently wrapped into the BiocSingular package for ease of use and package development. Specifically, we can change the SVD algorithm used in any of these functions by simply specifying an alternative value for the BSPARAM argument.

R

library(scater)
library(BiocSingular)

# As the name suggests, it is random, so we need to set the seed.
set.seed(101000)

r.out <- runPCA(sce, ncomponents = 20, BSPARAM = RandomParam())

str(reducedDim(r.out, "PCA"))

OUTPUT

 num [1:2411, 1:20] 14.79 5.79 13.07 -32.19 -26.45 ...
 - attr(*, "dimnames")=List of 2
  ..$ : chr [1:2411] "cell_9769" "cell_9770" "cell_9771" "cell_9772" ...
  ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...
 - attr(*, "varExplained")= num [1:20] 192.6 87 29.4 23.1 21.6 ...
 - attr(*, "percentVar")= num [1:20] 25.84 11.67 3.94 3.1 2.89 ...
 - attr(*, "rotation")= num [1:500, 1:20] -0.174 -0.173 -0.157 0.105 -0.132 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:500] "ENSMUSG00000055609" "ENSMUSG00000052217" "ENSMUSG00000069919" "ENSMUSG00000048583" ...
  .. ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...

R

set.seed(101001)

i.out <- runPCA(sce, ncomponents = 20, BSPARAM = IrlbaParam())

str(reducedDim(i.out, "PCA"))

OUTPUT

 num [1:2411, 1:20] -14.79 -5.79 -13.07 32.19 26.45 ...
 - attr(*, "dimnames")=List of 2
  ..$ : chr [1:2411] "cell_9769" "cell_9770" "cell_9771" "cell_9772" ...
  ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...
 - attr(*, "varExplained")= num [1:20] 192.6 87 29.4 23.1 21.6 ...
 - attr(*, "percentVar")= num [1:20] 25.84 11.67 3.94 3.1 2.89 ...
 - attr(*, "rotation")= num [1:500, 1:20] 0.174 0.173 0.157 -0.105 0.132 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:500] "ENSMUSG00000055609" "ENSMUSG00000052217" "ENSMUSG00000069919" "ENSMUSG00000048583" ...
  .. ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...

Both IRLBA and randomized SVD (RSVD) are much faster than the exact SVD and usually yield only a negligible loss of accuracy. This motivates their default use in many scran and scater functions, at the cost of requiring users to set the seed to guarantee reproducibility. IRLBA can occasionally fail to converge and require more iterations (passed via maxit= in IrlbaParam()), while RSVD involves an explicit trade-off between accuracy and speed based on its oversampling parameter (p=) and number of power iterations (q=). We tend to prefer IRLBA as its default behavior is more accurate, though RSVD is much faster for file-backed matrices.

Challenge

The uncertainty from approximation error is sometimes aggravating. “Why can’t my computer just give me the right answer?” One way to alleviate this feeling is to quantify the approximation error on a small test set like the sce we have here. Using the ExactParam() class, visualize the error in PC1 coordinates compared to the RSVD results.

Show me the solution

This code block calculates the exact PCA coordinates. Another thing to note: PC vectors are only identified up to a sign flip. We can see that the RSVD PC1 vector points in the

R

set.seed(123)

e.out <- runPCA(sce, ncomponents = 20, BSPARAM = ExactParam())

str(reducedDim(e.out, "PCA"))

OUTPUT

 num [1:2411, 1:20] -14.79 -5.79 -13.07 32.19 26.45 ...
 - attr(*, "dimnames")=List of 2
  ..$ : chr [1:2411] "cell_9769" "cell_9770" "cell_9771" "cell_9772" ...
  ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...
 - attr(*, "varExplained")= num [1:20] 192.6 87 29.4 23.1 21.6 ...
 - attr(*, "percentVar")= num [1:20] 25.84 11.67 3.94 3.1 2.89 ...
 - attr(*, "rotation")= num [1:500, 1:20] 0.174 0.173 0.157 -0.105 0.132 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:500] "ENSMUSG00000055609" "ENSMUSG00000052217" "ENSMUSG00000069919" "ENSMUSG00000048583" ...
  .. ..$ : chr [1:20] "PC1" "PC2" "PC3" "PC4" ...

R

reducedDim(e.out, "PCA")[1:5,1:3]

OUTPUT

                 PC1       PC2        PC3
cell_9769 -14.793684 18.470324 -0.4893474
cell_9770  -5.789032 13.347277  5.0560761
cell_9771 -13.066503 16.803152 -0.5602737
cell_9772  32.185950  6.697517 -0.6945423
cell_9773  26.452390  3.083474 -0.2271916

R

reducedDim(r.out, "PCA")[1:5,1:3]

OUTPUT

                 PC1       PC2        PC3
cell_9769  14.793780 18.470111 -0.4888676
cell_9770   5.789148 13.348438  5.0702153
cell_9771  13.066327 16.803423 -0.5562241
cell_9772 -32.186341  6.698347 -0.6892421
cell_9773 -26.452373  3.083974 -0.2299814

For the sake of visualizing the error we can just flip the PC1 coordinates:

R

reducedDim(r.out, "PCA") = -1 * reducedDim(r.out, "PCA")

From there we can visualize the error with a histogram:

R

error <- reducedDim(r.out, "PCA")[,"PC1"] - 
         reducedDim(e.out, "PCA")[,"PC1"]

data.frame(approx_error = error) |> 
  ggplot(aes(approx_error)) + 
  geom_histogram()

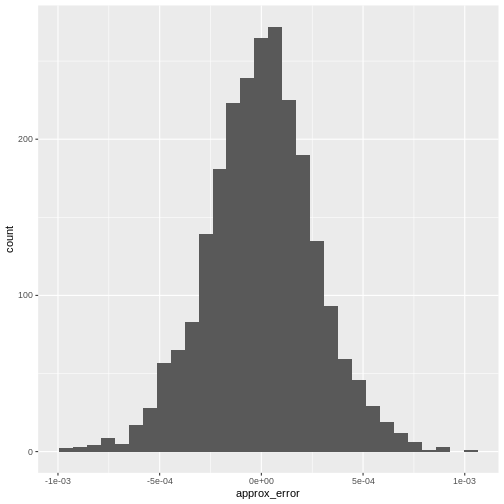
It’s almost never more than .001 in this case.

Interoperability with popular single-cell analysis ecosytems

---

Seurat

Seurat is an R package designed for QC, analysis, and exploration of single-cell RNA-seq data. Seurat can be used to identify and interpret sources of heterogeneity from single-cell transcriptomic measurements, and to integrate diverse types of single-cell data. Seurat is developed and maintained by the Satija lab and is released under the MIT license.

R

library(Seurat)

Although the basic processing of single-cell data with Bioconductor packages (described in the OSCA book) and with Seurat is very similar and will produce overall roughly identical results, there is also complementary functionality with regard to cell type annotation, dataset integration, and downstream analysis. To make the most of both ecosystems it is therefore beneficial to be able to easily switch between a SeuratObject and a SingleCellExperiment. See also the Seurat conversion vignette for conversion to/from other popular single cell formats such as the AnnData format used by scanpy.

Here, we demonstrate converting the Seurat object produced in Seurat’s PBMC tutorial to a SingleCellExperiment for further analysis with functionality from OSCA/Bioconductor. We therefore need to first install the SeuratData package, which is available from GitHub only.

R

BiocManager::install("satijalab/seurat-data")

We then proceed by loading all required packages and installing the PBMC dataset:

R

library(SeuratData)

InstallData("pbmc3k")

We then load the dataset as an SeuratObject and convert it to a SingleCellExperiment.

R

# Use PBMC3K from SeuratData
pbmc <- LoadData(ds = "pbmc3k", type = "pbmc3k.final")

pbmc <- UpdateSeuratObject(pbmc)

pbmc

pbmc.sce <- as.SingleCellExperiment(pbmc)

pbmc.sce

Seurat also allows conversion from SingleCellExperiment objects to Seurat objects; we demonstrate this here on the wild-type chimera mouse gastrulation dataset.

R

sce <- WTChimeraData(samples = 5, type = "processed")

assay(sce) <- as.matrix(assay(sce))

sce <- logNormCounts(sce)

sce

After some processing of the dataset, the actual conversion is carried out with the as.Seurat function.

R

sobj <- as.Seurat(sce)

Idents(sobj) <- "celltype.mapped"

sobj

Scanpy

Scanpy is a scalable toolkit for analyzing single-cell gene expression data built jointly with anndata. It includes preprocessing, visualization, clustering, trajectory inference and differential expression testing. The Python-based implementation efficiently deals with datasets of more than one million cells. Scanpy is developed and maintained by the Theis lab and is released under a BSD-3-Clause license. Scanpy is part of the scverse, a Python-based ecosystem for single-cell omics data analysis.

At the core of scanpy’s single-cell functionality is the anndata data structure, scanpy’s integrated single-cell data container, which is conceptually very similar to Bioconductor’s SingleCellExperiment class.

Bioconductor’s zellkonverter package provides a lightweight interface between the Bioconductor SingleCellExperiment data structure and the Python AnnData-based single-cell analysis environment. The idea is to enable users and developers to easily move data between these frameworks to construct a multi-language analysis pipeline across R/Bioconductor and Python.

R

library(zellkonverter)

The readH5AD() function can be used to read a SingleCellExperiment from an H5AD file. Here, we use an example H5AD file contained in the zellkonverter package.

R

example_h5ad <- system.file("extdata", "krumsiek11.h5ad",
                            package = "zellkonverter")

readH5AD(example_h5ad)

OUTPUT

class: SingleCellExperiment
dim: 11 640
metadata(2): highlights iroot
assays(1): X
rownames(11): Gata2 Gata1 ... EgrNab Gfi1
rowData names(0):
colnames(640): 0 1 ... 158-3 159-3
colData names(1): cell_type
reducedDimNames(0):
mainExpName: NULL
altExpNames(0):

We can also write a SingleCellExperiment to an H5AD file with the writeH5AD() function. This is demonstrated below on the wild-type chimera mouse gastrulation dataset.

R

out.file <- tempfile(fileext = ".h5ad")

writeH5AD(sce, file = out.file)

The resulting H5AD file can then be read into Python using scanpy’s read_h5ad function and then directly used in compatible Python-based analysis frameworks.

Exercises

---

Exercise 1: Out of memory representation

Write the counts matrix of the wild-type chimera mouse gastrulation dataset to an HDF5 file. Create another counts matrix that reads the data from the HDF5 file. Compare memory usage of holding the entire matrix in memory as opposed to holding the data out of memory.

Give me a hint

See the HDF5Array function for reading from HDF5 and the writeHDF5Array function for writing to HDF5 from the HDF5Array package.

Show me the solution

R

wt_out <- tempfile(fileext = ".h5")

wt_counts <- counts(WTChimeraData())

writeHDF5Array(wt_counts,
               name = "wt_counts",
               file = wt_out)

OUTPUT

<29453 x 30703> sparse HDF5Matrix object of type "double":
                       cell_1     cell_2     cell_3 ... cell_30702 cell_30703
ENSMUSG00000051951          0          0          0   .          0          0
ENSMUSG00000089699          0          0          0   .          0          0
ENSMUSG00000102343          0          0          0   .          0          0
ENSMUSG00000025900          0          0          0   .          0          0
ENSMUSG00000025902          0          0          0   .          0          0
               ...          .          .          .   .          .          .
ENSMUSG00000095041          0          1          2   .          0          0
ENSMUSG00000063897          0          0          0   .          0          0
ENSMUSG00000096730          0          0          0   .          0          0
ENSMUSG00000095742          0          0          0   .          0          0
         tomato-td          1          0          1   .          0          0

R

oom_wt <- HDF5Array(wt_out, "wt_counts")

object.size(wt_counts)

OUTPUT

1520366960 bytes

R

object.size(oom_wt)

OUTPUT

2488 bytes

Exercise 2: Parallelization

Perform a PCA analysis of the wild-type chimera mouse gastrulation dataset using a multicore backend for parallel computation. Compare the runtime of performing the PCA either in serial execution mode, in multicore execution mode with 2 workers, and in multicore execution mode with 3 workers.

Give me a hint

Use the function system.time to obtain the runtime of each job.

Show me the solution

R

sce.brain <- logNormCounts(sce.brain)

system.time({i.out <- runPCA(sce.brain, 
                             ncomponents = 20, 
                             BSPARAM = ExactParam(),
                             BPPARAM = SerialParam())})

system.time({i.out <- runPCA(sce.brain, 
                             ncomponents = 20, 
                             BSPARAM = ExactParam(),
                             BPPARAM = MulticoreParam(workers = 2))})

system.time({i.out <- runPCA(sce.brain, 
                             ncomponents = 20, 
                             BSPARAM = ExactParam(),
                             BPPARAM = MulticoreParam(workers = 3))})

Further Reading

• OSCA book, Chapter 14: Dealing with big data
• The BiocParallel intro vignette.

Key Points

• Out-of-memory representations can be used to work with single-cell datasets that are too large to fit in memory.
• Parallelization of calculations across genes or cells is an effective strategy for speeding up analysis of large single-cell datasets.
• Fast approximations for nearest neighbor search and singular value composition can speed up essential steps of single-cell analysis with minimal loss of accuracy.
• Converter functions between existing single-cell data formats enable analysis workflows that leverage complementary functionality from poplular single-cell analysis ecosystems.

Session Info

---

R

sessionInfo()

OUTPUT

R version 4.4.2 (2024-10-31)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 22.04.5 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8
 [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8
 [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C
[10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C

time zone: UTC
tzcode source: system (glibc)

attached base packages:
[1] stats4    stats     graphics  grDevices utils     datasets  methods
[8] base

other attached packages:
 [1] zellkonverter_1.14.0         Seurat_5.1.0
 [3] SeuratObject_5.0.2           sp_2.1-4
 [5] BiocSingular_1.20.0          BiocNeighbors_1.22.0
 [7] bluster_1.14.0               scran_1.32.0
 [9] MouseGastrulationData_1.18.0 SpatialExperiment_1.14.0
[11] BiocParallel_1.38.0          scater_1.32.0
[13] ggplot2_3.5.1                scuttle_1.14.0
[15] TENxBrainData_1.24.0         HDF5Array_1.32.0
[17] rhdf5_2.48.0                 DelayedArray_0.30.1
[19] SparseArray_1.4.8            S4Arrays_1.4.1
[21] abind_1.4-5                  Matrix_1.7-0
[23] SingleCellExperiment_1.26.0  SummarizedExperiment_1.34.0
[25] Biobase_2.64.0               GenomicRanges_1.56.0
[27] GenomeInfoDb_1.40.1          IRanges_2.38.0
[29] S4Vectors_0.42.0             BiocGenerics_0.50.0
[31] MatrixGenerics_1.16.0        matrixStats_1.3.0
[33] BiocStyle_2.32.0

loaded via a namespace (and not attached):
  [1] spatstat.sparse_3.0-3     httr_1.4.7
  [3] RColorBrewer_1.1-3        tools_4.4.2
  [5] sctransform_0.4.1         utf8_1.2.4
  [7] R6_2.5.1                  lazyeval_0.2.2
  [9] uwot_0.2.2                rhdf5filters_1.16.0
 [11] withr_3.0.0               gridExtra_2.3
 [13] progressr_0.14.0          cli_3.6.2
 [15] formatR_1.14              spatstat.explore_3.2-7
 [17] fastDummies_1.7.3         labeling_0.4.3
 [19] spatstat.data_3.0-4       ggridges_0.5.6
 [21] pbapply_1.7-2             parallelly_1.37.1
 [23] limma_3.60.2              RSQLite_2.3.7
 [25] generics_0.1.3            ica_1.0-3
 [27] spatstat.random_3.2-3     dplyr_1.1.4
 [29] ggbeeswarm_0.7.2          fansi_1.0.6
 [31] lifecycle_1.0.4           yaml_2.3.8
 [33] edgeR_4.2.0               BiocFileCache_2.12.0
 [35] Rtsne_0.17                grid_4.4.2
 [37] blob_1.2.4                promises_1.3.0
 [39] dqrng_0.4.1               ExperimentHub_2.12.0
 [41] crayon_1.5.2              dir.expiry_1.12.0
 [43] miniUI_0.1.1.1            lattice_0.22-6
 [45] beachmat_2.20.0           cowplot_1.1.3
 [47] KEGGREST_1.44.0           magick_2.8.3
 [49] pillar_1.9.0              knitr_1.47
 [51] metapod_1.12.0            rjson_0.2.21
 [53] future.apply_1.11.2       codetools_0.2-20
 [55] leiden_0.4.3.1            glue_1.7.0
 [57] data.table_1.15.4         vctrs_0.6.5
 [59] png_0.1-8                 spam_2.10-0
 [61] gtable_0.3.5              cachem_1.1.0
 [63] xfun_0.44                 mime_0.12
 [65] survival_3.6-4            statmod_1.5.0
 [67] fitdistrplus_1.1-11       ROCR_1.0-11
 [69] nlme_3.1-164              bit64_4.0.5
 [71] filelock_1.0.3            RcppAnnoy_0.0.22
 [73] BumpyMatrix_1.12.0        irlba_2.3.5.1
 [75] vipor_0.4.7               KernSmooth_2.23-24
 [77] colorspace_2.1-0          DBI_1.2.3
 [79] tidyselect_1.2.1          bit_4.0.5
 [81] compiler_4.4.2            curl_5.2.1
 [83] basilisk.utils_1.16.0     plotly_4.10.4
 [85] scales_1.3.0              lmtest_0.9-40
 [87] rappdirs_0.3.3            stringr_1.5.1
 [89] digest_0.6.35             goftest_1.2-3
 [91] spatstat.utils_3.0-4      rmarkdown_2.27
 [93] basilisk_1.16.0           XVector_0.44.0
 [95] htmltools_0.5.8.1         pkgconfig_2.0.3
 [97] sparseMatrixStats_1.16.0  highr_0.11
 [99] dbplyr_2.5.0              fastmap_1.2.0
[101] rlang_1.1.3               htmlwidgets_1.6.4
[103] UCSC.utils_1.0.0          shiny_1.8.1.1
[105] DelayedMatrixStats_1.26.0 farver_2.1.2
[107] zoo_1.8-12                jsonlite_1.8.8
[109] magrittr_2.0.3            GenomeInfoDbData_1.2.12
[111] dotCall64_1.1-1           patchwork_1.2.0
[113] Rhdf5lib_1.26.0           munsell_0.5.1
[115] Rcpp_1.0.12               viridis_0.6.5
[117] reticulate_1.37.0         stringi_1.8.4
[119] zlibbioc_1.50.0           MASS_7.3-60.2
[121] AnnotationHub_3.12.0      plyr_1.8.9
[123] parallel_4.4.2            listenv_0.9.1
[125] ggrepel_0.9.5             deldir_2.0-4
[127] Biostrings_2.72.1         splines_4.4.2
[129] tensor_1.5                locfit_1.5-9.9
[131] igraph_2.0.3              spatstat.geom_3.2-9
[133] RcppHNSW_0.6.0            reshape2_1.4.4
[135] ScaledMatrix_1.12.0       BiocVersion_3.19.1
[137] evaluate_0.23             renv_1.0.11
[139] BiocManager_1.30.23       httpuv_1.6.15
[141] RANN_2.6.1                tidyr_1.3.1
[143] purrr_1.0.2               polyclip_1.10-6
[145] future_1.33.2             scattermore_1.2
[147] rsvd_1.0.5                xtable_1.8-4
[149] RSpectra_0.16-1           later_1.3.2
[151] viridisLite_0.4.2         tibble_3.2.1
[153] memoise_2.0.1             beeswarm_0.4.0
[155] AnnotationDbi_1.66.0      cluster_2.1.6
[157] globals_0.16.3